A Bayesi ja sagedusliku statistika võrdlus

library(tidyverse)
library(rethinking)
library(ggthemes)
library(brms)

Kaks statistikat: ajaloost ja tõenäosusest

Bayesiaanlik ja sageduslik statistika leiutati üksteise järel Pierre-Simon Laplace poolt, kes arendas välja kõigepealt bayesiaanliku statistika alused ning seejärel sagedusliku statistika omad (ca. 1774 - 1814). Sagedusliku statistika õitsengu põhjusteks 20. sajandil olid arvutuslik lihtsus ning tõenäosuse sagedusliku tõlgenduse sobivus 20 saj esimeses pooles käibinud teadusfilosoofiatega - eeskätt loogilise postivismiga. 1930-1980-ndatel valitses akadeemiliste statistikute seas seisukoht, et Bayesiaanlik statistika on surnud ja maha maetud, ning selle arendamisega tegelesid vaid üksikud inimesed, kes sageli olid füüsikaliste teaduste taustaga (Jeffreys, Jaynes).

Alates 1960-e keskpaigast arendati bayesiaanlust USA sõjaväe egiidi all, kuna seal oli piisav juurdepääs arvutivõimsusele, kuid seda tehti paljuski salastatult. Bayesi meetoditega ei olnud võimalik korralikult tsiviilteadust teha enne 1990-ndaid aastaid, mil personaalarvutite levik algatas buumi nende meetodite arendamises. Praegu on maailmas bayesiaanlikku ja sageduslikku statistikat umbes pooleks (vähemalt uute meetodite arendustöö poole pealt). Eestis bayesiaanlik statistika 2017 aasta seisuga peaaegu, et puudub.

1930ndatel kodifitseeris Andrei Kolmogorov tõenäosusteooria aksioomid (3 aksioomi), mis ütlevad lühidalt, et tõenäosused jäävad 0 ja 1 vahele ning, et üksteist välistavate ja hüpoteesiruumi ammendavate hüpoteeside tõenäosused summeeruvad ühele. Selgus, et Bayesi teoreem on lihtsa aritmeetika abil tuletatav Kolmogorovi aksioomidest. Tagantjärele saame öelda, et bayesiaanlik statistika on mitte ainult tõenäosusteooriaga kooskõlas vaid ka, et Bayesi teoreem on parim võimalik viis sellist kooskõla saavutada (see on 1950ndate tarkus - Coxi teoreem). On ka teada, et kui tõenäosused on fikseeritud nulli ja ühega, siis taandub Bayesi teoreem klassikalisele lausearvutuslikule loogikale. See tähendab, et klassikaline loogika on bayesiaanluse erijuht. Seevastu sageduslik statistika püüab saavutada mõistlikke lahendusi arvutuslikult lihtsamate meetoditega, mille hinnaks on formaalse kooskõla puudumine tõenäosusteooriaga. Seega kujutab sageduslik statistika endast kogumit ad hoc meetodeid, mis ei tähenda muidugi, et sellest kasu ei võiks olla. Küll aga tähendab see, et kuigi sageduslike mudeleid on lihtsam arvutada, on neid raskem ehitada ja mõista ning, et sageduslike testide, milliseid on viimase saja aasta jooksul loodud 10 000 ringis, tulemusi on raskem tõlgendada.

Kahe statistika põhiline erinevus ei tulene tõenäosusteooria matemaatikast, vaid erinevatest tõenäosuse tõlgendusest.

Bayesi tõlgenduses on tõenäosus teadlase usu määr mingi hüpoteesi kehtimisse. Hüpotees võib näiteks olla, et järgmise juulikuu sademete hulk Vilsandil jääb vahemikku 22 kuni 34 mm. Kui Bayesi arvutus annab selle hüpoteesi tõenäosuseks 0.57, siis oleme me selle teadmise najal nõus maksma mitte rohkem kui 57 senti kihlveo eest, mille alusel makstakse juhul, kui see hüpotees tõeseks osutub, välja 1 EUR (ja me saame vähemalt 43 senti kasumit).

Sageduslikud teoreetikud usuvad, et selline tõenäosuse tõlgendus on ebateaduslik, kuna see on “subjektiivne”. Nimelt on võimalik, et n teadlast arvutavad samade andmete, kuid erinevate taustateadmiste põhjal n erinevat korrektset tõenäosust. Veelgi hullem, kui nad lähtuvad väga erinevatest taustauskumustest, ei pruugi toimuda teadmiste konvergeerumist ka siis, kui nende arvutustesse andmeid järjest juurde tuua.

Sellise olukorra osaline analoogia poliitikas on elanikkond, kus pooled kannavad konservatiivseid väärtusi (perekond, rahvusühtsus) ja teine pool liberaalseid (multikultuursus, üldinimlikud väärtused). Seega priorid on erinevad. Senikaua kui mõlemad pooled saavad oma uudised samast allikast (sama tõepära), ei ole demokraatia siiski ohus. Aga kui pooled hakkavad erinevatest allikatest hankima erinevaid fakte, mis kummagi ideoloogiat kinnitavad, toimub arvamuste polariseerumine ning demokraatia sattub ohtu.

Seega, kui te usute, et teie taustateadmised ei tohi mõjutada järeldusi, mis te oma andmete põhjal teete, siis te ei ole bayesiaan. Siinkohal pakub alternatiivi tõenäosuse sageduslik tõlgendus. Sageduslik tõenäosus on defineeritud kui teatud tüüpi andmete esinemise pikaajaline suhteline sagedus. Näiteks, kui me viskame münti palju kordi, siis peaks kullide (või kirjade) suhteline sagedus andma selle mündi tõenäosuse langeda kiri üleval. Selline tõenäosus on omistatav ainult sellistele sündmustele, mille esinemisel on sagedus. Kuna teaduslikul hüpoteesil ei ole esinemise sagedust, ei ole sageduslikus statistikas võimalik rääkida ka hüpoteesi kehtimise tõenäosusest. See on tõsine probleem, kuna tüüpiline statistiline hüpotees ütleb: meie mõõtmiste keskväärtus jääb vahemikku a kuni b – ja me tahaksime sellele anda usaldusintervallid, mis ütleksid, millise tõenäosusega see hüpotees kehtib. Sageduslik lahendus on selle asemel, et rääkida meie hüpoteesi tõenäosusest meie andmete korral, rääkida andmete, mis sarnanevad meie andmetega, esinemise tõenäosusest null-hüpoteesi (mis ei ole meie hüpotees) kehtimise korral. Seega omistatakse sagedus ehk tõenäosus andmetele, mitte hüpoteesile. Samas bayesiaan, kelle tõenäosused kehtivad hüpoteesidele, räägib otse tõenäosuse, millega parameetri väärtus jääb a ja b vahele, või ükskõik millisesse muusse teid huvitavasse vahemikku.

Poleemika: kumbki tõenäosus pole päris see, mida üldiselt arvatakse

Bayesi tõenäosus ei anna tegelikult seda tõenäosusnumbrit, mida me reaalselt peaksime kihlveokontoris kasutama. Ta annab numbri, millest me lähtuksime juhul, kui me usuksime, et selle numbri arvutamisel kasutatud statistilised mudelid kirjeldavad täpselt maailma. Paraku, kuna mudeldamine on oma olemuselt kompromiss mudeli lihtsuse ja ennustusvõime vahel, ei ole meil põhjust sellist asja uskuda. Seega ei peaks me bayesi tõenäosusi otse maailma üle kandma, vähemasti mitte automaatselt. Bayes ei ütle meile, mida me reaalselt usume. Ta ei ütle, mida me peaksime uskuma. Ta ütleb, mida me peaksime uskuma tingimuslikult.

Sageduslik tõenäosus on hoopis teine asi. Seda on võimalik vaadelda kahel viisil:

1. imaginaarsete andmete esinemissagedus nullhüpoteesi all;

2. reaalsete sündmuste esinemise sagedus.

Teise vaate kohaselt on sageduslik tõenäosus päriselt olemas. See on samasugune füüsikaline nähtus nagu näiteks auto kiirus, mõõdetuna liiklusmiilitsa poolt.

Kui kaks politseinikku mõõdavad sama auto kiirust ja 1. saab tulemuseks 81 km/h ning 2. saab 83 km/h, siis meie parim ennustus auto kiiruse kohta on 82 km/h. Kui aga 1. mõõtmistulemus on 80 km/h ja teine 120 km/h, siis meie parim hinnang ei ole 100 km/h. Enne sellise hinnangu andmist peame tegema lisatööd ja otsustama, kumb miilits oma mõõtmise kihva keeras. Ja me ei otsusta seda mitte oodatavast trahvist lähtuvalt, vaid neutraalseid objektiivseid asjaolusid vaagides. Seda sellepärast, et autol on päriselt kiirus olemas ja meil on hea põhjus, miks me tahame seda piisava täpsusega teada. Sagedusliku statistiku mõõteriist on statistiline mudel ja mõõtmistulemus on tõenäosus, mis jääb 0 ja 1 vahele.

Õpikunäidetes on sündmusteks, mille esinemise sagedust tõenäosuse abil mõõdetakse, enamasti täringuvisked, ehk katsesüsteemi reaalne füüsikaline funktsioneerimine. Pane tähele, et need on inimtekkelised sündmused (loodus – ega jumal – ei viska täringuid). Teaduses on sündmused, millele tõenäosusi omistatakse, samuti inimtekkelised: selleks sündmuseks on teadlase otsus H₀ ümber lükkamise kohta, mille tegemisel ta lähtub p (või q) väärtusest ja usaldusnivoost. Siin vastab auto kiirusele 1. tüüpi vigade tegemise sagedus. See sagedus on inimtekkeline, aga sellest hoolimata päriselt olemas ja objektiivselt mõõdetav. Kui 2 teadlast mõõdavad seda paraleelselt ja saavad piisavalt erineva tulemuse (näiteks väga erineva FDR-i), võib olla kindel, et vähemalt üks neist eksib, ning peaks olema võimalik ausalt otsustada, kumb.

Võrdlev näide: kahe grupi võrdlus

Järgnevalt toome näite, kuidas bayesiaan ja sageduslik statistik lahendavad sama ülesande. Meil on 2 gruppi, katse ja kontroll, millest kummagis 30 mõõtmist ja me soovime teada, kui palju katsetingimus mõjutab mõõtmistulemust. Meie andmed on normaaljaotusega ja andmepunktid, mida me analüüsime, on efektisuurused (katse1 - kontroll1 = ES1 jne).

Bayesiaan

Statistiline küsimus on Bayesiaanil ja sageduslikul statistikul sama: kas ja kui palju erinevad kahe grupi keskväärtused? Bayesiaan alustab sellest, et ehitab kaks mudelit: andmete tõepäramudel ja taustateadmiste mudel ehk prior.

Kui andmed on normaaljaotusega, siis on ka tõepäramudel normaaljaotus. Alustame sellest, et fitime oma valimiandmed (üksikud efekti suurused) normaaljaotuse mudelisse.

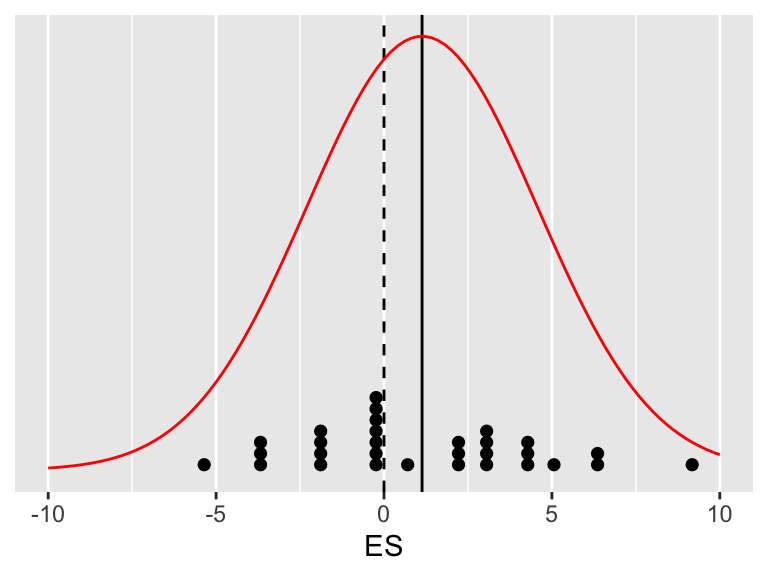
Joonis A.1: Paariviisiline katse - kontroll disain. Katset on korratud 30 korda. X-teljel on efektisuurused (ES). 30 üksikut efektisuurust on näidatud punktidena. Must joon näitab keskmist efektisuurust. Andmed on mudeldatud normaaljaotusena.

See ei ole veel tõepäramudel, sest me tahame hinnangut ES keskväärtuse kõige tõenäolisemale väärtusele, ja lisaks veel hinnangut ebakindlusele selle punkt-hinnangu ümber (usalduslpiire). Seega tuleb eelmine jaotus kitsamaks tõmmata, et ta kajastaks meie teadmisi ES-ide keskväärtuste, mitte individuaalsete ES-de, kohta. Uue jaotusmudeli sd = eelmise jaotuse sd/sqrt(30).

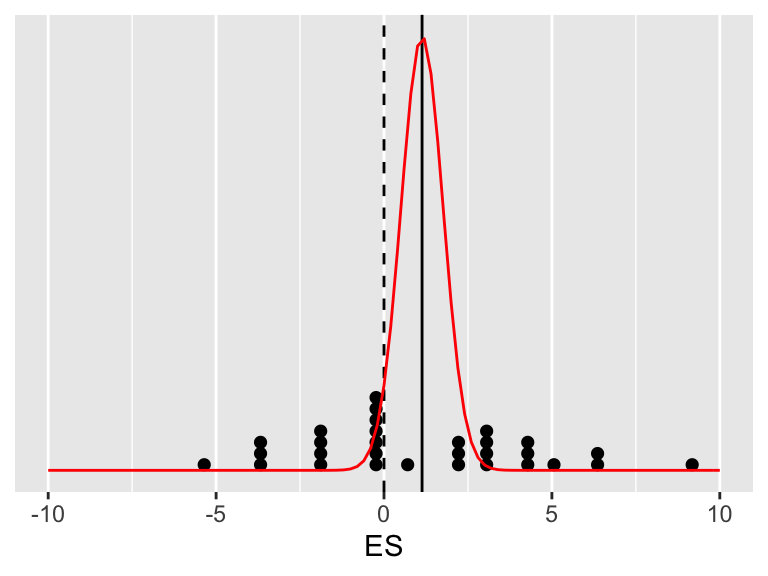
Joonis A.2: See jaotus iseloomustab keskmise ES paiknemist puhtalt meie andmete põhjal.

Täpsemalt, selle joonise põhjal võib arvutada, milline on meie valimi keskväärtuse kohtamise tõenäosus igal võimalikul tõelisel ES-i väärtusel. Kõige tõenäolisemad on andmed siis, kui tegelik ES = andmete keskväärtusega (seda kohta näitab must joon). Kui me jagame musta joone pikkuse punase kurvi all läbi katkendjoone pikkusega sama kurvi all, saame teada, mitu korda on meie andmed tõenäolisemad siis, kui tegelik ES = mean(valimi ES), võrreldes olukorraga, kus tegelik ES = 0. Loomulikult võime sama näitaja arvutada ükskõik millise hüpoteeside paari kohta (näiteks, andmed on miljon korda tõenäolisemad hüpoteesi ES = 0.02 all kui hüpoteesi ES = -1 all; mis aga ei tähenda, et andmed oleksid väga tõenäolised kummagi võrreldud hüpoteesi all).

Aga see ei ole veel Bayes. Lisame andmemudelile taustateadmiste mudeli. Sellega tühistame me väga olulise eelduse, mis ripub veskikivina sagedusliku statistika kaelas. Nimelt, et valimi andmed peavad olema esinduslikud populatsiooni suhtes. Me võime olla üsna kindlad, et väikeste valimite korral see eeldus ei kehti ja sellega seoses ei tööta ka sageduslik statistika viisil, milleks R.A. Fisher selle kunagi lõi. Taustateadmiste mudeli peamine, kuigi mitte ainus, roll on mõjutada meie hinnangut õiges suunas vähendades halbade andmete võimet meile kahju teha. Kui sul on väike valim, siis sinu andmed vajavad sellist kantseldamist.

Olgu meie taustateadmise mudel normaaljaotus keskväärtusega 0 ja standardhälbega 1.

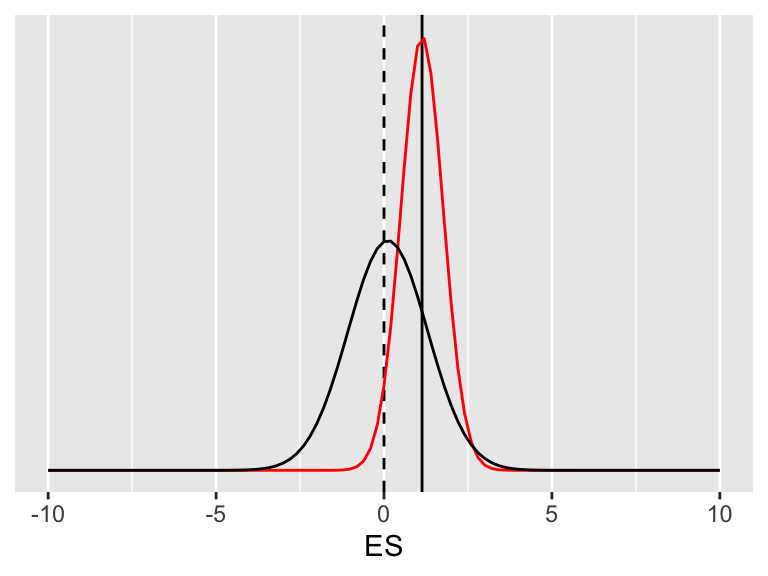
Joonis A.3: Taustateadmiste mudel ehk prior on normaaljaotus (must joon), mille ülesanne on veidi vähendada ekstreemsete valimite kahjulikku mõju.

Taustateadmiste mudel on sageli normaaljaotus. Kui meil on palju taustateadmisi, siis on see jaotus kõrge ja kitsas, kui meil on vähe taustateadmisi, siis on see madal ja lai.

Mida teha, kui sa ei taha, et taustateadmiste mudel sinu posteeriori kuju mõjutab? Sellisel juhul kasutatakse nõrgalt informatiivseid prioreid, mis tähendab, et priori jaotus on palju laiem kui tõepäramudeli laius. Miks mitte kasutada mitte-informatiivseid tasaseid prioreid? Põhjused on arvutuslikud, seega tehnilist laadi.

Igal juhul järgmise sammuna korrutab bayesiaan selle jaotuse andmejaotusega, saades tulemuseks kolmanda normaaljaotuse, mille ta seejärel normaliseerib nii, et jaotuse alune pindala = 1. See kolmas jaotus on posterioorne tõenäosusjaotus, mis sisaldab kogu infot, millest saab arvutada kõige tõenäolisema katseefekti suuruse koos ebakindluse määraga selle ümber (mida rohkem andmeid, seda väiksem ebakindlus) ja tõenäosused, et tegelik katseefekt jääb ükskõik milllisesse meid huvitavasse vahemikku.

Nüüd ei ole siis muud kui bayesi mudel läbi arvutada.

dfa <- data.frame(a)
m99 <- map2stan(
  alist(
    a ~ dnorm(mean = mu, sd = sigma),
    mu  ~ dnorm(0, 1), 
    sigma ~ dcauchy(0, 1)), 
  data = dfa)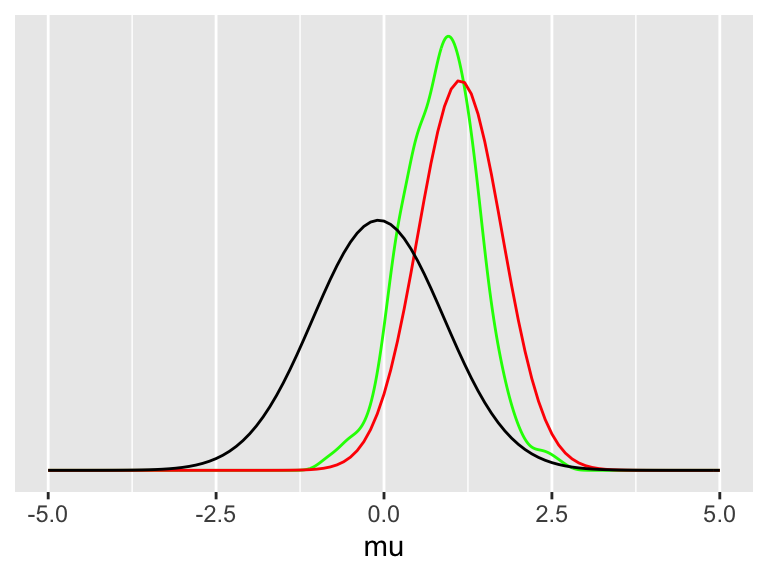

Joonis A.4: Triplot. Bayesi väljund on posterioorne tõenäosusjaotus (roheline). Nagu näha, ei ole selle jaotuse tipp täpselt samas kohas kui andmejaotuse tipp ehk keskväärtus. Prior tõmbab seda veidi nulli suunas. Lisaks on posteerior veidi kitsam kui andmemudel, mis tähendab, et hinnang ES-le tuleb väiksema ebakindluse määraga.

Posteerior sisaldab endas kogu infot, mis meil ES-i tõelise väärtuse kohta on. Siit saame arvutada:

1. parima hinnangu ES-i punktväärtusele,

2. usaldusintervalli, ehk millisest ES-ide vahemikust loodame leida tõelise ES-i näit 90% tõenäosusega,

3. iga mõeldava ES-i väärtuste vahemiku kohta tõenäosuse, millega tõeline ES jääb sellesse vahemikku.

4. saame ES-i põhjal arvutada mõne muu statistiku, näiteks ES1 = log(ES), kasutades selleks ES-i posterioorset jaotust. Sel viisil kanname oma ES-i hinnangus peituva ebakindluse üle ES1-le, millele saame samuti rakendada punkte 1-3 (sest ES1 on posterioorne jaotus).

5. uute andmete lisandumisel saame kasutada ES-i posteeriorit uue priorina ja arvutada uue täiendatud posteeriori. Põhimõtteliselt võime seda teha pärast iga üksiku andmepunkti lisandumist. See avab ka head võimalused metaanalüüsiks.

6. lisaks saame oma algsest mudelist ka posteeriori andmepunkti tasemel varieeruvusele (pole näidatud). Seda kasutame uute andmete simuleerimiseks (meie näites üksikud ES-d).

Sageduslik statistik

Sageduslik lähenemine sisaldab ainult ühte mudelit, mida võrreldakse valimi andmetega. Sageduslik statistik alustab selles lihtsas näites täpselt samamoodi nagu bayesiaan, tekitades eelmisega identse andmemudeli, mis on keskendatud valimi keskväärtusele A.2. Seejärel nihutab ta oma andmemudelit niipalju, et normaaljaotuse tipp ei ole enam valimi keskväärtuse kohal vaid hoopis 0-efekti kohal. Jaotuse laius nihutamisel ei muutu.

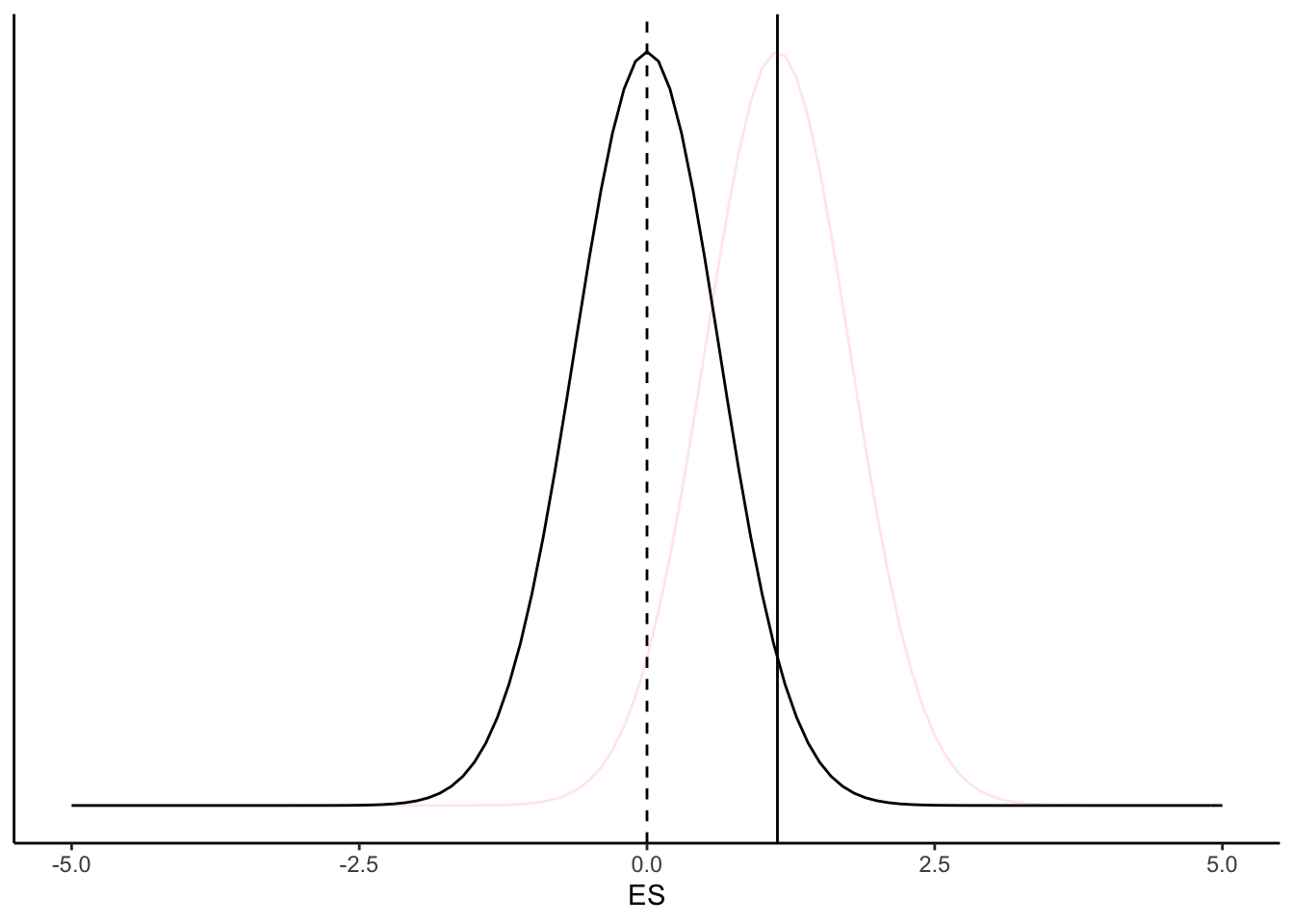
Joonis A.5: Nullhüpotees (must kõver) ja tõepärafunktsioon (punane kõver).

Seda nullile tsentreeritud mudelit kutsutakse null-hüpoteesiks (H₀). Nüüd võrdleb ta oma valimi keskväärtust (must joon) H₀ jaotusega. Kui valimi keskväärtuse kohal on H₀ jaotus kõrge, siis on andmete tõenäosus H₀ kehtimise korral suur. Ja vastupidi, kui valimi keskväärtuse kohal on H₀ madal, siis on andmete esinemise tõenäosus H₀ all madal. Seda tõenäosust kutsutakse p väärtuseks. Mida väiksem on p, seda vähem tõenäolised on teie andmed juhul, kui H~0 on tõene ja katseefekt võrdub nulliga. P on defineeritud kui “teie andmete või 0-st veel kaugemal asuvate andmete esinemise pikaajaline suhteline sagedus tingimusel, et H₀ kehtib”.

Tulemuste tõlgendamine

Kui sageduslik statistik kirjutab, et tema “efekti suurus on statistiliselt oluline 0.05 olulisusnivool”, siis ta ütleb sellega, et tema poolt arvutatud p < 0.05. Selle väite korrektne tõlgendus on, et juhul kui statistik pika aja jooksul võtab omaks “statistiliselt olulistena” kõik tulemused, millega kaasnev p < 0.05 ja lükkab tagasi kõik tulemused, mille p > 0.05, siis sooritab ta 5% sagedusega 1. tüüpi vigu. See tähendab, et igast sajast tõesest H~0-st, mida ta testib, võtab ta keskeltläbi 5 vastu, kui statistiliselt olulised. Sageduslik statistika on parim viis 1. tüüpi vigade sageduse fikseerimiseks.

Paraku ei tea me ühegi üksiku testi kohta ette, kas see testib kehtivat või mittekehtivat H₀-i, mis teeb raskeks katseseeriate ühekaupa tõlgendamise. Tuletame meelde, et sageduslikus statistikas ei saa rääkida H₀ kehtimise tõenäosusest vaid peab rääkima andmete tõenäosusest (ehk andmete esinemise sagedusest) tingimusel, et H₀ kehtib.

Kas ühte p väärtust saab tõlgendada kui hinnangut tõendusmaterjali hulgale, mida teie valim pakub H₀ vastu? Selle üle on vaieldud juba üle 80 aasta, kuid tundub, et ainus viis seda kas või umbkaudu teha on bayesiaanlik. Igal juhul, p väärtust, mis on defineeritud pikaajalise sagedusena, on raske rakendada üksiksündmusele. Bayesiaanliku p väärtuste tõlgendamiskalkulaatori leiate aadressilt http://www.graphpad.com/quickcalcs/interpretPValue1/.

Kujutle mass spektroskoopia katset, kus mõõdame 2000 valgu tasemeid katse-kontroll skeemis ja katset korratakse n korda. Sageduslik statistik kasutab adjusteeritud p väärtusi või q väärtusi, et tõmmata piir, millest ühele poole jäävad statistiliselt olulised ES-d ja teisele poole mitteolulised null-efektid. Edasi tõlgendab ta mitteolulisi efekte kui ebaolulisi ja diskuteerib vaid “olulisi” efekte. Paraku, p väärtuste arvutamine ja adjusteerimine saab toimuda mitmel erineval moel ja usalduspiiri panekule just 95-le protsendile, mitte näiteks 89% või 99.2%-le, pole ühtegi ratsionaalset põhjendust. Seega tõmbab ta sisuliselt juhuslikus kohas joone läbi efektide, misjärel ignoreerib kõiki sellest joonest valele poole jäänud efekte. Meetod, mis väga hästi töötab pikaajalises kvaliteedikontrollis, ei ole kahjuks kuigi mõistlik katse tulemuste ükshaaval tõlgendamises. Mis juhtub, kui oleme kavalad ja proovime mitmeid erinevaid p väärtustega töötamise meetodeid, et valida välja see usalduspiir, millest õigele poole jäävaid andmeid on teaduslikult kõige parem tõlgendada? Ehkki ükshaaval võisid kõik meie poolt läbi arvutatud meetodid olla lubatud (ja isegi võrdselt head), ei fikseeri p nüüd enam 1. tüüpi vigade sagedust. See tähendab, et p on kaotanud definitsioonijärgse tähenduse ja te oleksite võinud olulisuspiiri sama hästi tõmmata tunde järgi.

Tüüpiline tulemuse kirjeldus artiklis:

1. sageduslik: the effect is statistically significant (p < 0.01).

2. bayesiaanlik: the most likely effect size is xxx (90% CI = xxx-low, xxx-high) and the probability that the true effect is < 0 is xxx percent.

90% CI — credible interval — tähendab, et me oleme 90% kindlad, et tegelik efekti suurus asub meie poolt antud vahemikus.

Kahe paradigma erinevused

1. sageduslikus statistikas võrdub punkt-hinnang tegelikule efekti suurusele valimi keskmise ES-ga. Bayesi statistikas see sageli nii ei ole, sest taustateadmiste mudel mõjutab seda hinnangut. Paljud mudelid püüavad ekstreemseid valimeid taustateadmiste abil veidi mõistlikus suunas nihutada, niiviisi vähendades ülepaisutatud efektide avaldamise ohtu.

2. sageduslik statistika töötab tänu sellele, et uurija võtab vastu pluss-miinus otsuseid: iga H~0 kas lükatakse ümber või jäetakse kehtima. Seevastu bayesiaan mõtleb halli varjundites: sissetulevad andmed kas suurendavad või vähendavad hüpoteeside tõenäosusi (mis jäävad aga alati > 0 ja < 1).

3. p väärtused kontrollivad 1. tüüpi vigade sagedust ainult siis, kui katse disaini ja hilisema tulemuste analüüsi detailid on enne katse sooritamist fikseeritud (või eelnevalt on täpselt paika pandud lubatud variatsioonid katse- ja analüüsi protokollis). Eelkõige tähendab see, et valimi suurus ja kasutatavad statistilinsed testid peavad olema eelnevalt fikseeritud. Tüüpiliselt saame p väärtuse arvutada vaid üks kord ja kui p = 0.051, siis oleme sunnitud H~0 paika jätma ning efekti deklareerimisest loobuma. Me ei saa lihtsalt katset juurde teha, et vaadata, mis juhtub. Bayesiaan seevastu võib oma posterioorse tõenäosuse arvutada kasvõi pärast iga katsepunkti kogumist ning katse peatada kohe (või alles siis), kui ta leiab, et tema posterioorne jaotus on piisavalt kitsas, et teaduslikku huvi pakkuda.

4. Sageduslikus statistikas sõltub tulemus sellest, kas hüpotees, mida testitakse oli defineeritud enne andmete kogumist või mitte. Selle pärast tuleks seal testitavad hüpoteesid eel-registreerida. Bayesi statistikas pole aga vahet, kas hüpotees on formuleeritud enne või pärast andmete nägemist – seal loevad tõepärafunktiooni loomisel ainult olemasolevad andmed (mitte andmed, mis oleksid võinud olla aga ei ole).

5. sagedusliku statistika pluss-miinus iseloom tingib selle, et kui tegelik efekti suurus on liiga väike, et sattuda õigele poole olulisusnivood, siis annavad statistiliselt olulisi tulemusi ülepaisutatud efektid, mida tekib tänu valimiveale. Nii saab süstemaatiliselt kallutatud teaduse. Bayesi statistikas seda probleemi ei esine, kuna otsused ei ole pluss-miinus tüüpi.

6. bayesi statistika ei fikseeri 1. tüüpi vigade sagedust. See-eest võitleb see nn valehäirete vastu, milleks kaasajal kasutatakse enim mitmetasemelisi shrinkage mudeleid. See on bayesi vaste sageduslikus statistikas kasutatavatele mitmese testimise korrektsioonidele. Kui sageduslik statistik võitleb valehäiretega p väärtusi adjusteerides ja selle läbi olulisusnivood nihutades, siis bayesiaan kasutab shrinkage mudelit, et parandada hinnanguid üksikute efektide keskväärtustele ja nende sd-le, kasutades paindlikult kogu andmestikus leiduvat infot.

Sageduslik ja teaduslik hüpoteesitestimine

Teaduslik lähenemine tõendusmaterjalile on sarnane kohtuliku uurimisega: me kogume tõendusmaterjali senikaua, kuni oleme veendunud, et saame selle põhjal eelistada ühte hüpoteesi kõikide teiste arvelt. Seega, kui faktid meile piisavat survet avaldavad, võtame vastu pluss-miinus otsuse, et kohtualune süüdi või teaduslik hüpotees õigeks mõista. See otsus on meie tegevuse eesmärk ja meie tegevus oli suunatud selle eesmärgi täitmisele.

Sageduslik statistika võtab samuti vastu dihhotoomseid otsuseid, aga hoopis teisel moel. Seal ei ole otsus eesmärk, vaid vahend. Kui me lükkame tagasi teatud null hüpoteesid, aga mitte teised, saame me sellisel viisil fikseerida pikaajalise 1. tüüpi vigade sageduse. Me võtame vastu otsuseid, eesmärgiga tagada katsesüsteemi pikaajaline kvaliteet. Need otsused ei eelda, et me usuksime, et mõni konkreetne null hüpotees on tõene või väär ning matemaatilised protseduurid, mille alusel me neid otsuseid langetame, ei püüa määrata individuaalse null hüpoteesi tõelähedust või tõenäosust, et see H~0 ei kehti. Seega ei tähenda fakt, et me lükkasime ümber konkreetse nullhüpoteesi seda, et me usume, et see null hüpotees on väär.

H₀-i ümber lükkamisel põhineva statistikaga kaasnevad järelmid, millest ehk olulisim on vajadus fikseerida andmete kogumise ja analüüsi meetodid enne, kui andmed on kogutud. See on nii tehnilistel põhjustel, mis on seotud puhtalt meie sooviga fikseerida 1. tüüpi vigade sagedus. Sellise veasageduste fikseerimise hind on, et andmeanalüüsi valikud ei saa sõltuda tegelikest andmetest (nende kvaliteedist, jaotusest jms). Siinkohal tuleb eraldi rõhutada, et tegemist ei ole üldise teadusliku meetodi omadusega. Teaduses (ja bayesi statistikas) on mitte ainult täiesti normaalne vaid lausa vajalik vaadata andmeid kriitilise pilguga ja kujundada oma analüüs vastavalt andmete kvaliteedile. Ning kui andmed ei paku piisavalt tõendusmaterjali, et me saaksime otsustada oma hüpoteesi kasuks või kahjuks, siis on igati mõistlik andmeid juurde korjata senikaua, kuni oleme veendunud ühte või teistpidi.

Oluline erinevus sagedusliku ja bayesi statistika vahel on, et kui sageduslik meetod fikseerib pikaajalise veasageduse aga ei arvuta üksikute hüpoteeside tõenäosust, siis bayesi meetod vastupidi arvutab üksikute hüpoteeside tõenäosused, aga ei fikseeri pikaajalisi veasagedusi. Kui meid ikkagi huvitavad veasagedused ja statistiline võimsus, saab neid ka bayesiaanlikult leida, arvutades oma mudeleid simuleeritud andmetega.

Statistiline ennustus kui mitmetasandiline protsess

Me võime vaadelda ennustavat statistikat mitmetasemelise protsessina, kus alumisel tasemel on punkthinnang parameetri väärtusele, selle peal oleval tasemel on hinnang ebakindlusele selle punkthinnangu ümber, ning 3. tasemel on omakorda hinnang ebakindlusele 2. taseme hinnangu ümber. Ja nii edasi lõpmatusse. Bayes erineb klassikalisest statistikast selle poolest, et kui Bayes ehitab 2. taseme hinnangu tõepära ja priori põhjal, siis klassikaline statistika kasutab selleks pelgalt tõepära (konverteerituna null hüpoteesiks). See on tähtis, kuna tõepära modelleerib ainult seda osa juhuslikust varieeruvusest punkthinnangu ümber, mida kutsutakse valimiveaks. Prior on võimeline arvesse võtma ka andmete kallutatust.

Kuna klassikalises statistikas ei ole formaalset priori mudelit, ei hinda klassikalised usaldusintervallid (2. tase) tõelist ebakindlust punktväärtuse ümber. Seda teevad bayesiaanlikud kredibiilsusintervallid, aga ainult siis, kui priorite koostamisse on tõsiselt suhtutud.

I Punkthinnang – enamasti aritmeetiline keskmine –- modelleerib andmejaotuse tüüpilist elementi. Eeldus: me teame, milline on andmete jaotus.

II tõepärafunktsioon hindab ebakindlust punkthinnangu ümber. Modelleerib valimiviga, mis on seda suurem, mida vähem on teil andmeid. Eeldus 1: andmed on esinduslikud (andmejaotus = populatsiooni jaotus) Eeldus 2: mudel kirjeldab andmeid genereerivat mehhanismi (siit tulevad sageli lisaeeldused, nagu populatsiooni normaaljaotus, lineaarsus, sõltumatud sündmused valimi koostamisel, vigade sõltumatus, homoskedastilisus jms)

III prior kohendab tõepärafunktsiooni hinnangut Modelleerib (1) andmete esinduslikkust, mis on seda väiksem, mida väiksem on valim, ja (2) süstemaatilist viga. Eeldus: meil on oma andmetest sõltumatuid teadmisi populatsiooni jaotuse kohta

Kui valim on piisavalt suur, siis võime olla piisavalt kindlad, et andmed on esinduslikud ning klassikalise statistika hinnangud ebakindlusele punktväärtuse ümber muutuvad selle võrra usutavamaks.
Samas, sedamõõda kui valimi suurus kasvab, muutub tõepärafunktsioon üha kitsamaks, mis tõstab omakorda tõenäosust, et tegelik parameetri väärtus jääb tõepärafunktsiooni kõrgema osa alt välja, tingituna süstemaatilisest veast, mille suurus ei sõltu valimi suurusest. Seega töötab klassikaline statistika parimini keskmiselt suurte valimite (ja keskmiselt suure andmete varieeruvuse) korral.

A.0.1 Ajaloolist juttu: normaaljaotus, Bayes ja sageduslik statistika

(Anders Hald; A History of Parametric Statistical Inference from Bernoulli to Fisher, 1713-1935, Springer 2000)

Laplace sõnastas 1774. aastal statistiku tööpõllu järgmiselt: kirjeldamaks andmeid (vigade jaotust) tõenäosusfunktsioonina leia matemaatiline mudel, millel oleks lõplik arv parameetreid. Seejärel leia algoritm, mis minimeeriks vead meie hinnagutele nende parameetrite väärtuste kohta. Seega oli eesmärk konverteerida andmete (mõõtmisvigade) jaotus posterioorseks tõenäosusjaotuseks, mille pealt saaks omakorda arvutada usaldusintervallid meie hinnagu täpsusele.

Laplace, kes tegeles palju astronoomilste mõõtmiste analüüsiga, lootis näidata, et mõõtmisandmete aritmeetiline keskmine on parim viis arvutada sellise posterioorse jaotuse kõige tõenäolisemat väärtust (lokatsiooniparameetrit). Parim viis selles mõttes, et teoreetiliselt parima lokalisatsiooniparameetri ümber on võimalik arvutada kitsaimad veapiirid. Aritmeetilise keskmise selle pärast, et selle kasutamine oli laialt levinud, tundus intuitiivselt mõistlik ning oli arvutuslikult lihtne. Laplace probleemi lahendas Gauss ca. 1809, võttes kasutusele nii uue tõenäosusjaotuse – normaaljaotuse – kui ka uue lokatsiooniparameetri arvutusmeetodi – vähimruutude meetodi. Tema küsitud küsimus oli: millist jaotust ja hindamismeetodit oleks vaja kasutada, et lokatsiooniparameeter tuleks just aritmeetiline keskmine? Rõhutades normaaljaotuse tähtsust, leidis Laplace 1812. aastal, et kõikidest sümmetrilistest andmejaotustest viib ainult normaaljaotus olukorrani, kus aritmeetiline keskmine kattub posterioorse jaotuse tipuga.

Kuna Laplace ei teadnud midagi tegelike veajaotuste kohta astronoomilistel mõõtmistel, oli tal raskusi andmejaotuse spetsifitseerimisega, mille pealt Bayesi teoreemiga posterioorne hinnanguvigade jaotus arvutada. Mõõtmisvigu tavatseti mudeldada nelinurksete, kolmnurksete või kvadraat-jaotustega ja polnud ühtki teaduslikku põhjust eelistada üht jaotust teistele. See oli üks põhjuseid, miks Laplace hakkas arendama sageduslikku statistikat ja kasutas alates 1811 üha vähem Bayesi teoreemi. (Alles 1818 näitas Bessel empiiriliselt, et astronoomilised mõõtmised on normaaljaotusega.) Teine põhjus hüljata Bayesi statistika oli seotud tehniliste raskustega priorite mudeldamisel, mistõttu Laplace oli sunnitud kasutama tasaseid prioreid, mis omistasid igale sündmusele/hüpoteesile võrdse eeltõenäosuse – ja oma ilmses absurdsuses tegid elu lihtsaks tema kriitikutele.

Sageduslik statistika kasutab oma alusena keskset piirteoreemi (Laplace 1810, 1812), mille kohaselt on paljude andmevalimite aritmeetilised keskmised normaaljaotusega, ja seda hoolimata andmete tegelikust jaotusest (eeldusel, et valimid on piisavalt suured; vt 6. ptk). Seega, senikaua kuni me ei modelleeri mitte ühe valimi empiirilist andmete jaotust (mida vajab Bayesi teoreem), vaid hoopis paljude virtuaalsete valimite pealt arvutatud keskväärtuste jaotust, ei pea me teadma, milline on andmete tegelik jaotus. Sellelt pinnalt ongi välja töötatud nullhüpoteesi testimine, millel põhineb suur osa 20. sajandi statistikast. 1908 näitas Edgeworth, et suurte valimite ja mitteinformatiivsete priorite korral annavad mõlemad meetodid (Bayes ja sageduslik) sama hinnangu parameetriväärtusele ja numbriliselt sama usaldusintervalli.

Sagedusliku statistika põhiprintsiibid: Fisher 1922.

Statistilisete meetodite eesmärk on andmete redutseerimine. Selleks on vaja vaadelda andmeid juhuvalimina hüpoteetilisest lõpmata suurest populatsioonist, mille jaotust saab kirjeldada suhteliselt väheste parameetritega mudeli abil. (Valimit iseloomustab “statistik”, populatsiooni aga “parameeter”)

Statistik puutub kokku kolme sorti probleemidega:

1. Spetsifikatsiooni probleemid kerkivad esile seoses populatsiooni jaotusmudeli spetsifitseerimisega.

2. Estimatsiooni probleemid kerkivad esile seoses algoritmidega, mille abil määratakse hüpoteetilise populatsioonimudeli parameetrite väärtused.

3. Jaotuse probleemid kerkivad üles seoses valimite põhjal arvutatud statistikute jaotuste matemaatilise kirjeldamisega.

Heal estimatsioonil on omakorda kolm kriteeriumit:

1. Konsistentsus — statistik on kosnsistentne siis, kui arvutatuna lõpmata suurest valimist, mis võrdub populatsiooniga, tuleb selle statistiku väärtus täpselt õige.

2. Efektiivsus — statistiku efektiivsus on suhe (protsent) selle sisemisest täpsusest võrrelduna teoreetiliselt efektiivseima statistikuga. Efektiivsus väljendab, kui suurt osa kogu kättesaadavast informatsioonist meie statistik kasutab. Efektiivsuse kriteerium: statistik, arvutatuna suurest valimist, annab vähima võimaliku standardhälbega normaaljaotuse.

3. Piisavus (sufficiency) — kriteerium: statistik on piisav kui ükski teine statistik, mida saab samast valimist arvutada, ei lisa informatsiooni hinnatava parameetri väärtuse kohta.

Fisheri poolt juurutatud sageduslik terminoloogia: parameeter, statistik, tõepära, dispersioon (variance; ANOVA), konsistentsus, efektiivsus, piisavus, informatsioon, null hüpotees, statistiline olulisus, p väärtus, olulisuse test, protsendipunkt, randomiseerimine, interaktsioon, faktoriaalne disain.

Tänu kesksele piirteoreemile on sageduslik statistika arvutuslikult palju lihtsam kui Bayesi statistika (arvutused saab teha paberi ja pliiatsiga), aga kuna me ei saa enam rääkida tegelike empiiriliste andmete jaotusest, vaid peame selle asemel kasutama lõpmata hulka virtuaalseid valimeid, ei saa me enam Bayesi teoreemi abil tõenäosusi pöörata (konverteerida meie andmete tõenäosus parameetriväärtuse x kehtimise korral, parameetriväärtuse x kehtimise tõenäosuseks meie andmete korral). Veelgi enam, me ei saa isegi rääkida meie andmete tõenäosusest parameetriväärtuse x kehtimise korral, vaid oleme sunnitud oma keelt ja meelt murdes rääkima “meie andmete või neist ekstreemsemate andmete pikajalisest suhtelisest sagedusest nullhüpoteesi (aga kahjuks mitte ühegi teise parameetriväärtuse) kehtimise korral” (Fisher ca. 1920). Nagu näha, on siin arvutuslikul lihtsusel kõrge kontseptuaalne hind.