13 Bayesi põhimõte

Bayesi arvutuseks on meil vaja teada

1. milline on “parameter space” ehk parameetriruum? Parameetriruum koosneb kõikidest loogiliselt võimalikest parameetriväärtustest. Näiteks kui me viskame ühe korra münti, koosneb parameetriruum kahest elemendist: 0 ja 1, ehk null kulli ja üks kull. See ammendab võimalike sündmuste nimekirja. Kui me aga hindame mõnd pidevat suurust (keskmine pikkus, tõenäosus 0 ja 1 vahel jms), koosneb parameetriruum lõpmata paljudest elementidest (arvudest).

2. milline on “likelihood function” ehk tõepärafunktsioon? Me omistame igale parameetriruumi elemendile (igale võimalikule parameetri väärtusele) tõepära. Tõepära parameetri väärtusel x on tõenäosus, millega me võiksime kohata oma andmete keskväärtust, juhul kui x oleks see ainus päris õige parameetri väärtus. Teisisõnu, tõepära on kooskõla määr andmete ja parameetri väärtuse x vahel. Tõepära = \(P(andmed~\vert~parameetri~v\ddot{a}\ddot{a}rtus)\). Näiteks, kui tõenäolised on meie andmed, kui USA keskmine president on juhtumisi 183.83629 cm pikkune? Kuna meil on vaja modeleerida tõepära igal võimalikul parameetri väärtusel (mida pideva suuruse puhul on lõpmatu hulk), siis kujutame tõepära pideva funktsioonina (näiteks normaaljaotusena), mis täielikult katab parameetriruumi. Tõepärafunktsioon ei summeeru 100-le protsendile — see on normaliseerimata.

3. milline on “prior function” ehk prior? Igale tõepära väärtusele peab vastama priori väärtus. Seega, kui tõepära on modelleeritud pideva funktsioonina, siis on ka prior pidev funktsioon (aga prior ei pea olema sama tüüpi funktsioon, kui tõepära). Erinevus tõepära ja priori vahel seisneb selles, et kui tõepärafunktsioon annab just meie andmete keskväärtuse tõenäosuse igal parameetriväärtusel, siis prior annab iga parameetriväärtuse tõenäosuse, sõltumata meie andmetest. See-eest arvestab prior kõikide teiste relevantsete andmetega, sünteesides taustateadmised ühte tõenäousmudelisse. Me omistame igale parameetriruumi väärtusele eelneva tõenäosuse, et see väärtus on üks ja ainus tõene väärtus. Prior jaotus summeerub 1-le. Prior kajastab meie konkreetsetest andmetest sõltumatut arvamust, kui suure tõenäosusega on just see parameetri väärtus tõene; seega seda, mida me usume enne oma andmete nägemist. Nendel parameetri väärtustel, kus prior (või tõepära) = 0%, on ka posteerior garanteeritult 0%. See tähendab, et kui te olete 100% kindel, et mingi sündmus on võimatu, siis ei suuda ka mäekõrgune hunnik uusi andmeid teie uskumust muuta (eelduselt, et te olete ratsionaalne inimene).

http://optics.eee.nottingham.ac.uk/match/uncertainty.php aitab praktikas priorit modelleerida (proovige Roulette meetodit).

Kui te eelnevast päriselt aru ei saanud, ärge muretsege. Varsti tulevad puust ja punaseks näited likelihoodi ja priori kohta.

Edasi on lihtne. Arvuti võtab tõepärafunktsiooni ja priori, korrutab need üksteisega läbi ning seejärel normaliseerib saadud jaotuse nii, et jaotusealune pindala võrdub ühega. Saadud tõenäosusjaotus ongi posteeriorne jaotus ehk posteerior ehk järeljaotus. Kogu lugu.

Me teame juba pool sajandit, et Bayesi teoreem on sellisele ülesandele parim võimalik lahendus. Lihtsamad ülesanded lahendame me selle abil täiuslikult. Kuna parameetrite arvu kasvuga mudelis muutub Bayesi teoreemi läbiarvutamine eksponentsiaalselt arvutusmahukamaks (sest läbi tuleb arvutada mudeli kõikide parameetrite kõikide väärtuste kõikvõimalikud kombinatsioonid), oleme sunnitud vähegi keerulisemad ülesanded lahendama umbkaudu, asendades Bayesi teoreemi ad hoc MCMC algoritmiga, mis teie arvutis peituva propelleri Karlsoni kombel lendu saadab, et tõmmata valim “otse” posterioorsest jaotusest. Meie poolt kasutatava MCMC Hamiltonian Monte Carlo mootori nimi on Stan (www.mc-stan.org). See on eraldiseisev programm, millel on R-i liides R-i pakettide rstan(), rethinking(), rstanarm() jt kaudu. Meie töötame ka edaspidi puhtalt R-s, mis automaatselt suunab meie mudelid ja muud andmed Stani, kus need läbi arvutatakse ja seejärel tulemused R-i tagasi saadetakse. Tulemuste töötlus ja graafiline esitus toimub jällegi R-is. Seega ei pea me ise kordagi Stani avama.

Alustame siiski lihtsa näitega, mida saab käsitsi läbi arvutada.

Esimene näide

Me teame, et suremus haigusesse on 50% ja meil on palatis 3 patsienti, kes seda haigust põevad. Seega on meil kaks andmetükki (50% ja n=3). Küsimus: mitu meie patsienti oodatavalt hinge heidavad? Eeldusel, et meie patsiendid on iseseisvad (näiteks ei ole sugulased), on meil tüüpiline mündiviske olukord.

Parameetriruum on neljaliikmeline: 0 surnud, 1 surnud, 2 surnud ja 3 surnud. Edasi loeme üles kõik võimalikud sündmusteahelad, mis loogiliselt saavad juhtuda, et saada tõepärafunktsioon.

Me viskame kulli-kirja 3 korda: kiri = elus, kull = surnud

Võimalikud sündmused on: | kull kull kull | kull kiri kull | kiri kull kull | kull kull kiri | kull kiri kiri | kiri kiri kull | kiri kull kiri | kiri kiri kiri

Kui P(kull) = 0.5, siis lugedes kokku kõik võimalikud sündmused:

• 0 kulli ehk surnud - 1,
• 1 kulli ehk surnud - 3,
• 2 kulli ehk surnud - 3,
• 3 kulli ehk surnud - 1

Nüüd teame parameetriruumi iga liikme kohta, kui suure tõenäosusega me ootame selle realiseerumist. Näiteks, P(0 surnud) = 1/8, P(1 surnud) = 3/8, P(1 või 2 surnud) = 6/8 jne Selle teadmise konverteerime tõepärafunktsiooniks.

library(tidyverse)
# Parameter space: all possible futures
x <- seq(from = 0, to = 3)

# Likelihoods for each x value, or P(deaths I x)
y <- c(1, 3, 3, 1)

ggplot(data=NULL, aes(x, y)) + 
  geom_point()+ 
  geom_line()+
  xlab("hypothetical nr of deaths")+ 
  ylab("plausibility")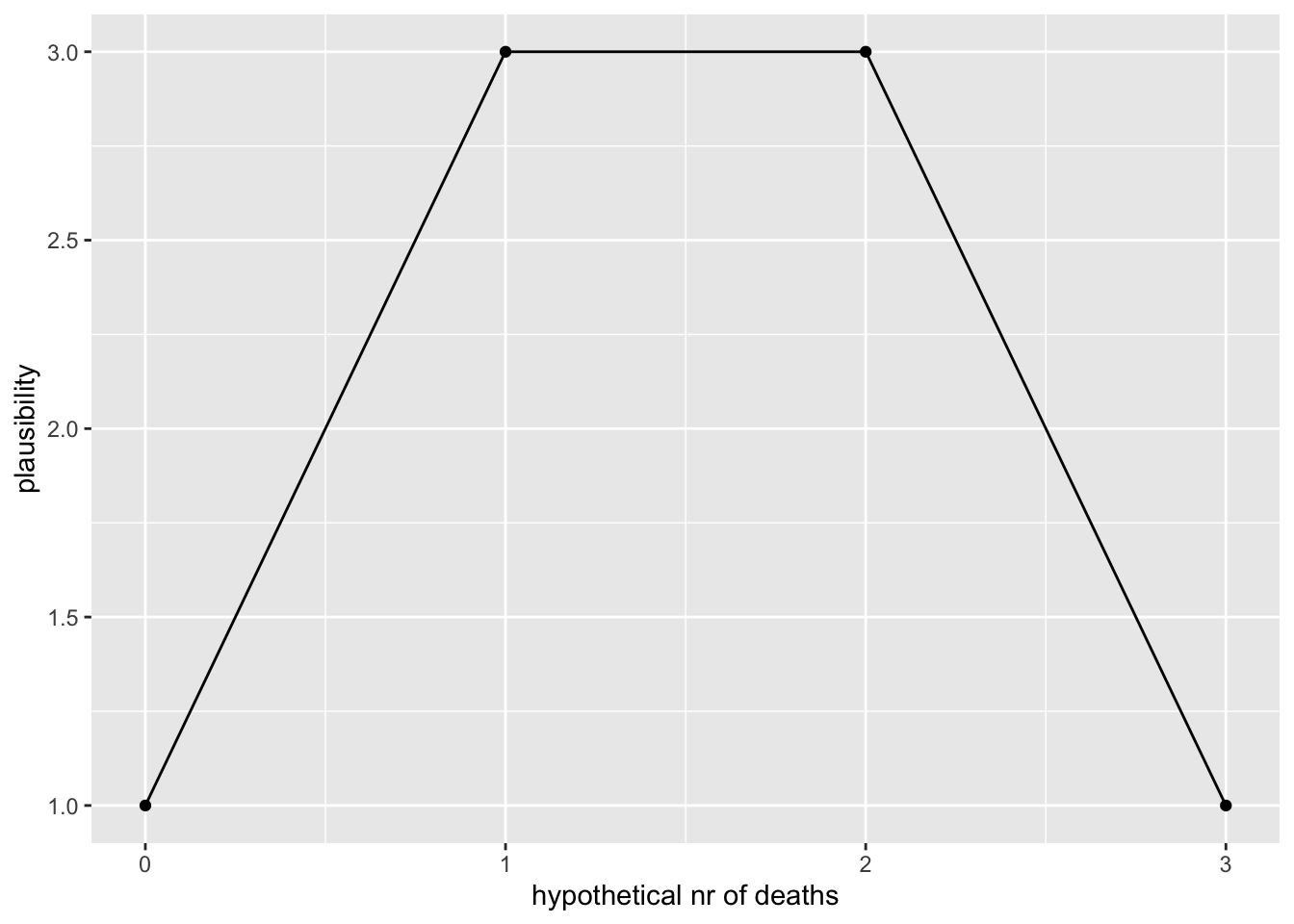

Siit näeme, et üks surm ja kaks surma on sama tõenäolised ja üks surm on kolm korda tõenäolisem kui null surma (või kolm surma). Tõepära annab meile tõenäosuse Pr(mortality=0.5 & N=3) igale loogiliselt võimalikule surmade arvule (0 kuni 3).

Me saame sama tulemuse kasutades formaalsel viisil binoomjaotuse mudelit. Ainus erinevus on, et nüüd on meil y teljel surmade tõenäosus.

y <- dbinom(x, 3, 0.5)

ggplot(data=NULL, aes(x, y)) + 
  geom_point()+
  geom_line()+
  xlab("hypothetical nr of deaths")+ 
  ylab("probability")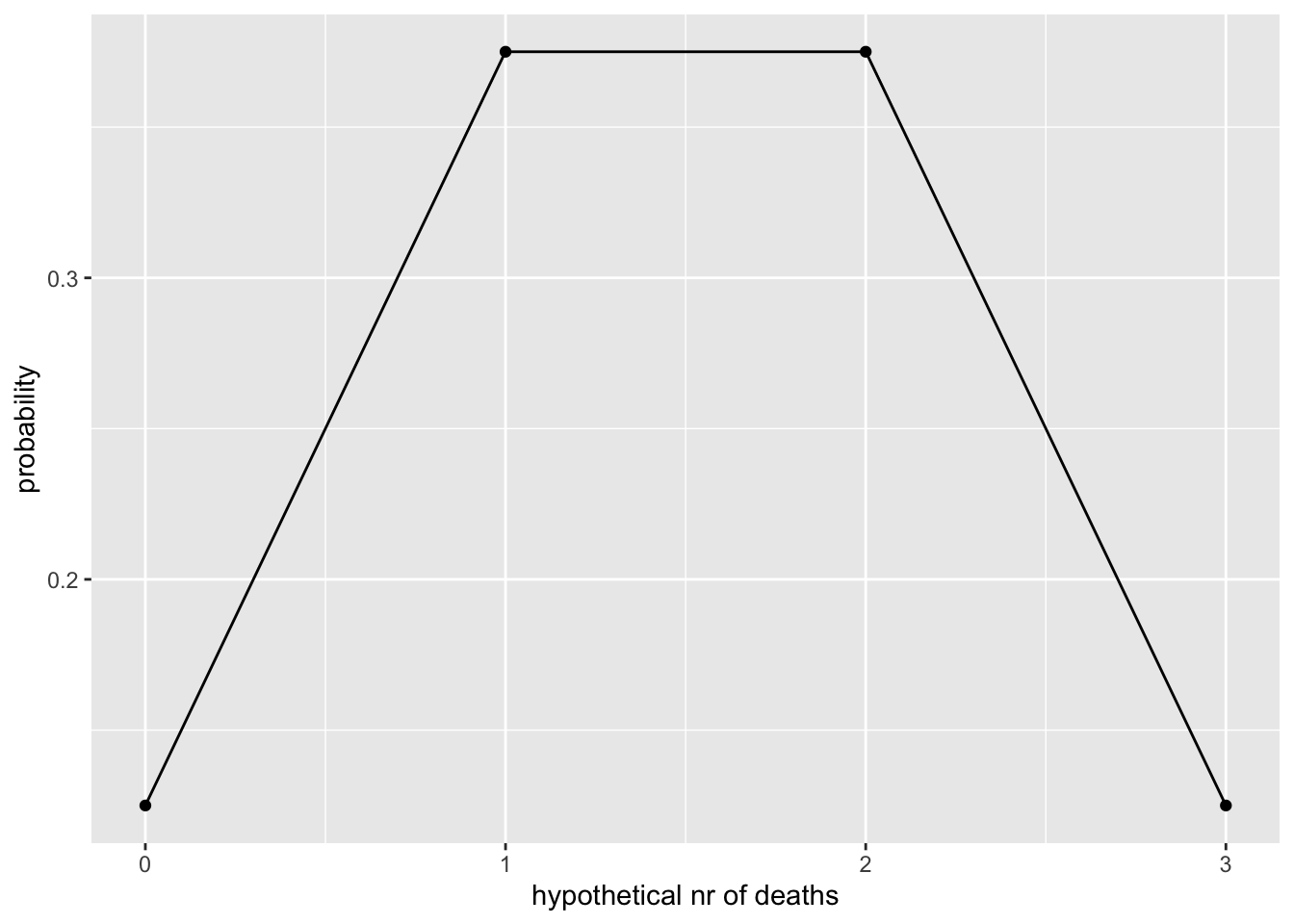

Proovime seda koodi olukorras, kus meil on 9 patsienti ja suremus on 0.67:

x <- seq(from = 0, to = 9)
y <- dbinom(x, 9, 0.67)

ggplot(data=NULL, aes(x, y)) + 
  geom_point()+
  geom_line()+
  xlab("hypothetical nr of deaths")+ 
  ylab("probability")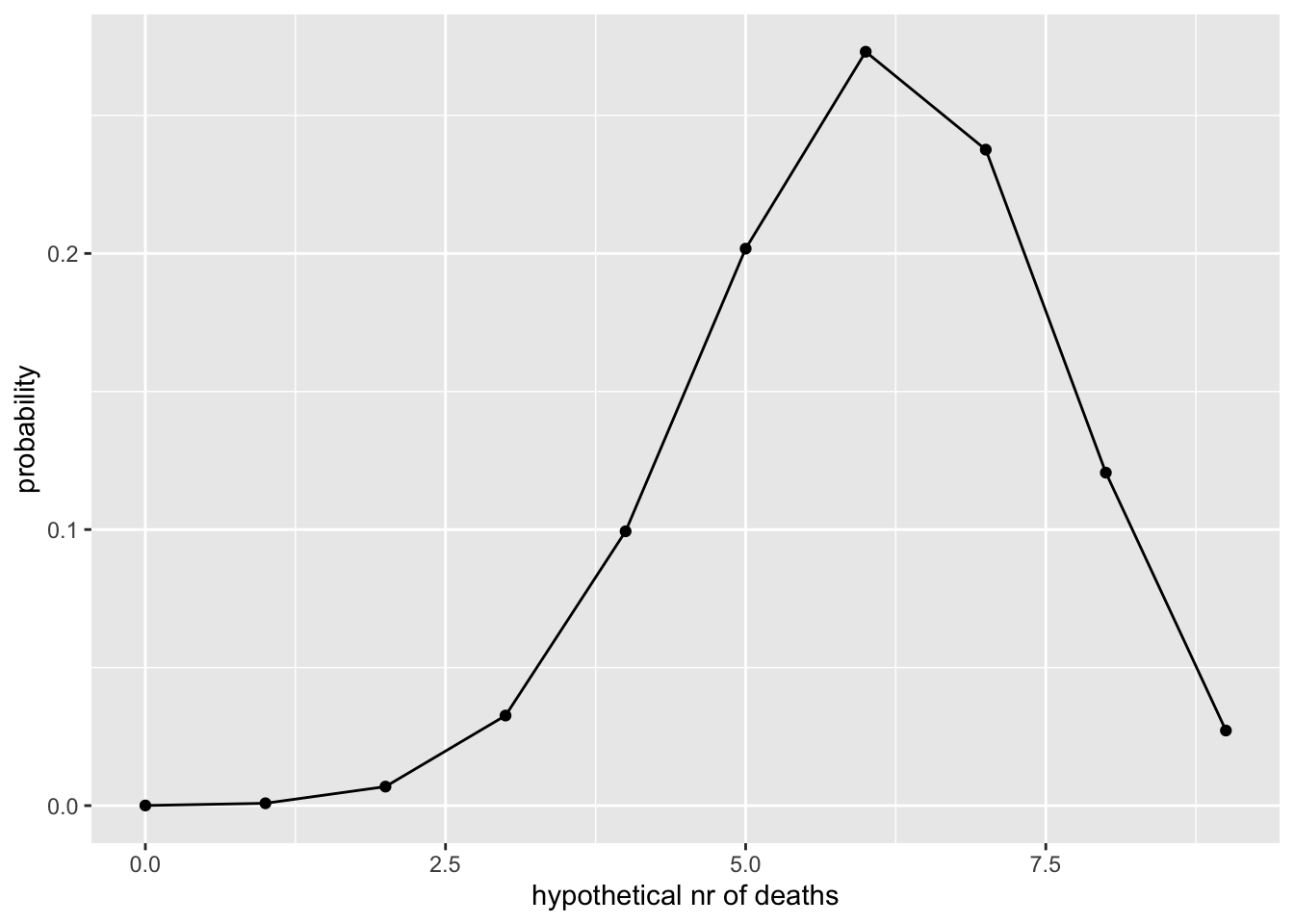

Lisame sellele tõepärafunktsioonile tasase priori (lihtsuse huvides) ja arvutame posterioorse jaotuse kasutades Bayesi teoreemi. Igale parameetri väärtusele on tõepära * prior proportsionaalne posterioorse tõenäosusega, et just see parameetri väärtus on see ainus tõene väärtus. Posterioorsed tõenäosused normaliseeritakse nii, et nad summeeruksid 1-le.

Me defineerime X telje kui rea 10-st arvust (0 kuni 9 surma) ja arvutame tõepära igale neist 10-st arvust. Sellega ammendame me kõik loogiliselt võimalikud parameetri väärtused.

x <- seq(from = 0 , to = 9)
# flat prior
prior <- rep(1 , 10)

# Compute likelihood at each value in grid
likelihood <- dbinom(x, size = 9, prob = 0.67)

# Compute product of likelihood and prior
unstd.posterior <- likelihood * prior

# Normalize the posterior, so that it sums to 1
posterior <- unstd.posterior / sum(unstd.posterior)

ggplot(data = NULL, aes(x, posterior)) + 
  geom_point() +
  geom_line() +
  xlab("hypothetical nr of deaths") + 
  ylab("posterior probability")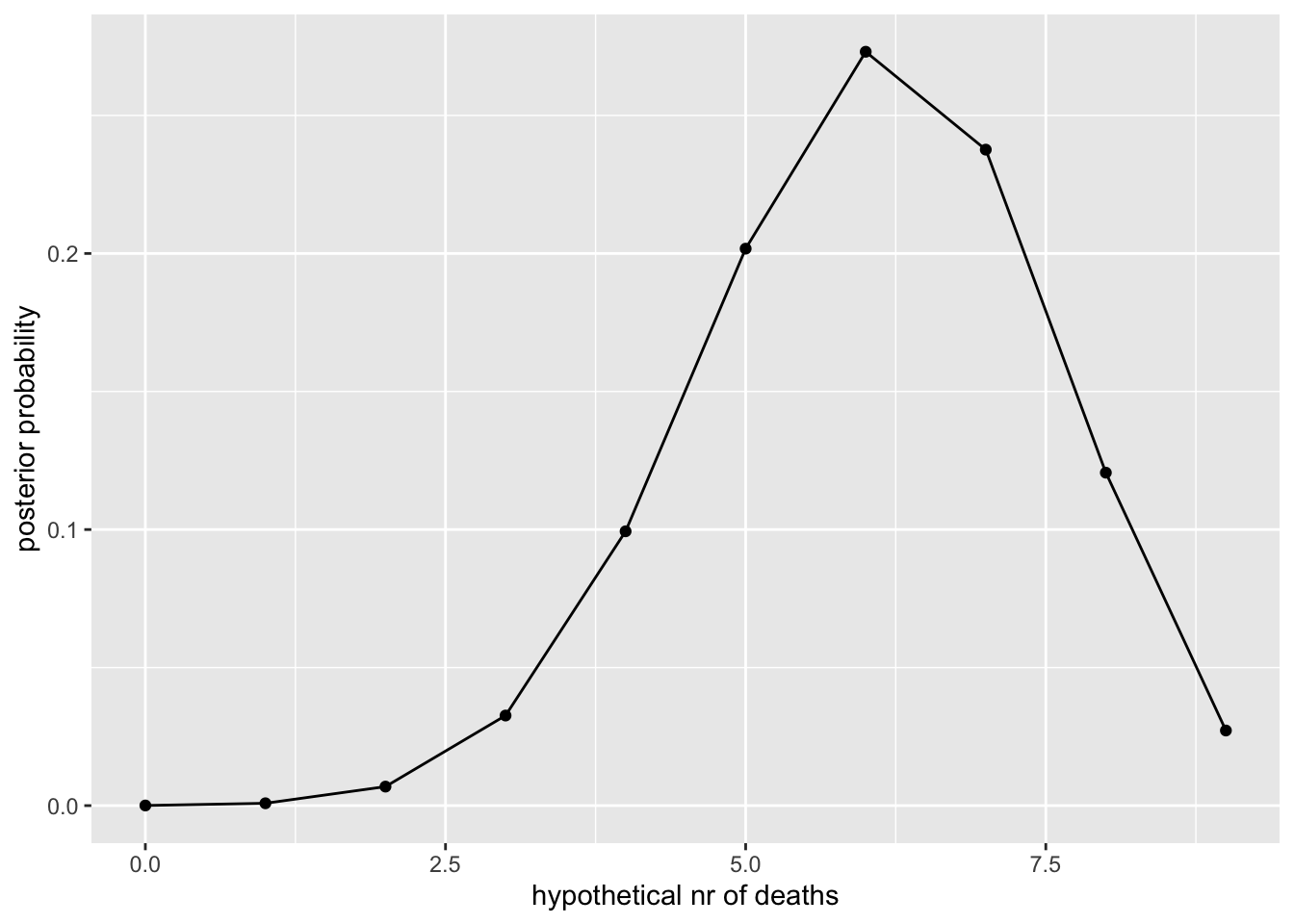

See on parim võimalik teadmine, mitu kirstu tasuks tellida, arvestades meie priori ja likelihoodi mudelitega. Näiteks, sedapalju, kui surmad ei ole üksteisest sõltumatud, on meie tõepäramudel (binoomjaotus) vale.

Teine näide: sõnastame oma probleemi ümber

Mis siis, kui me ei tea suremust ja tahaksime seda välja arvutada? Kõik, mida me teame on, et 6 patsienti 9st surid. Nüüd koosnevad andmed 9 patsiendi mortaalsusinfost (parameeter, mille väärtust me eelmises näites arvutasime) ja parameeter, mille väärtust me ei tea, on surmade üldine sagedus (see parameeter oli eelmises näites fikseeritud, ja seega kuulus andmete hulka).

Seega on meil:

1. Parameetriruum 0% kuni 100% suremus (0st 1-ni), mis sisaldab lõpmata palju numbreid.

2. Kaks võimalikku sündmust (surnud, elus), seega binoomjaotusega modelleeritud tõepärafunktsioon. Nagu me juba teame, on r funktsioonis dbinom() kolm argumenti: surmade arv, patsientide koguarv ja surmade tõenäosus. Seekord oleme me fikseerinud esimesed kaks ja soovime arvutada kolmanda väärtuse.

3. Tasane prior, mis ulatub 0 ja 1 vahel. Me valisime selle priori selleks, et mitte muuta tõepärafunktsiooni kuju. See ei tähenda, et me arvaksime, et tasane prior on mitteinformatiivne. Tasane prior tähendab, et me usume, et suremuse kõik väärtused 0 ja 1 vahel on võrdselt tõenäolised. See on vägagi informatsioonirohke (ebatavaline) viis maailma näha, ükskõik mis haiguse puhul!

Tõepära parameetri väärtusel x on tõenäosus kohata meie andmeid, kui x on juhtumisi parameetri tegelik väärtus. Meie näites koosneb tõepärafunktsioon tõenäosustest, et kuus üheksast patsiendist surid igal võimalikul suremuse väärtusel (0…1). Kuna see on lõpmatu rida, teeme natuke sohki ja arvutame tõepära 20-l valitud suremuse väärtusel.

Tehniliselt on sinu andmete tõepärafunktsioon agregeeritud iga üksiku andmepunkti tõepärafunktsioonist. Seega vaatab Bayes igat andmepunkti eraldi (andmete sisestamise järjekord ei loe).

# mortality at 20 evenly spaced probabilities from 0 to 1
x <- seq(from = 0 , to = 1, length.out = 20)

# Define prior
prior <- rep(1 , 20)

# Compute likelihood at each value in grid
likelihood <- dbinom(6, size = 9 , prob = x)

# Compute product of likelihood and prior & standardize the posterior
posterior <- likelihood * prior / sum(likelihood * prior)

#put everithing into a tibble for plotting
a <- tibble(x=rep(x=x, 3),
            y= c(prior, likelihood, posterior),
            legend= rep(c("prior","likelihood", "posterior"), each=20))

ggplot(data=a) + geom_line(aes(x, y, color=legend))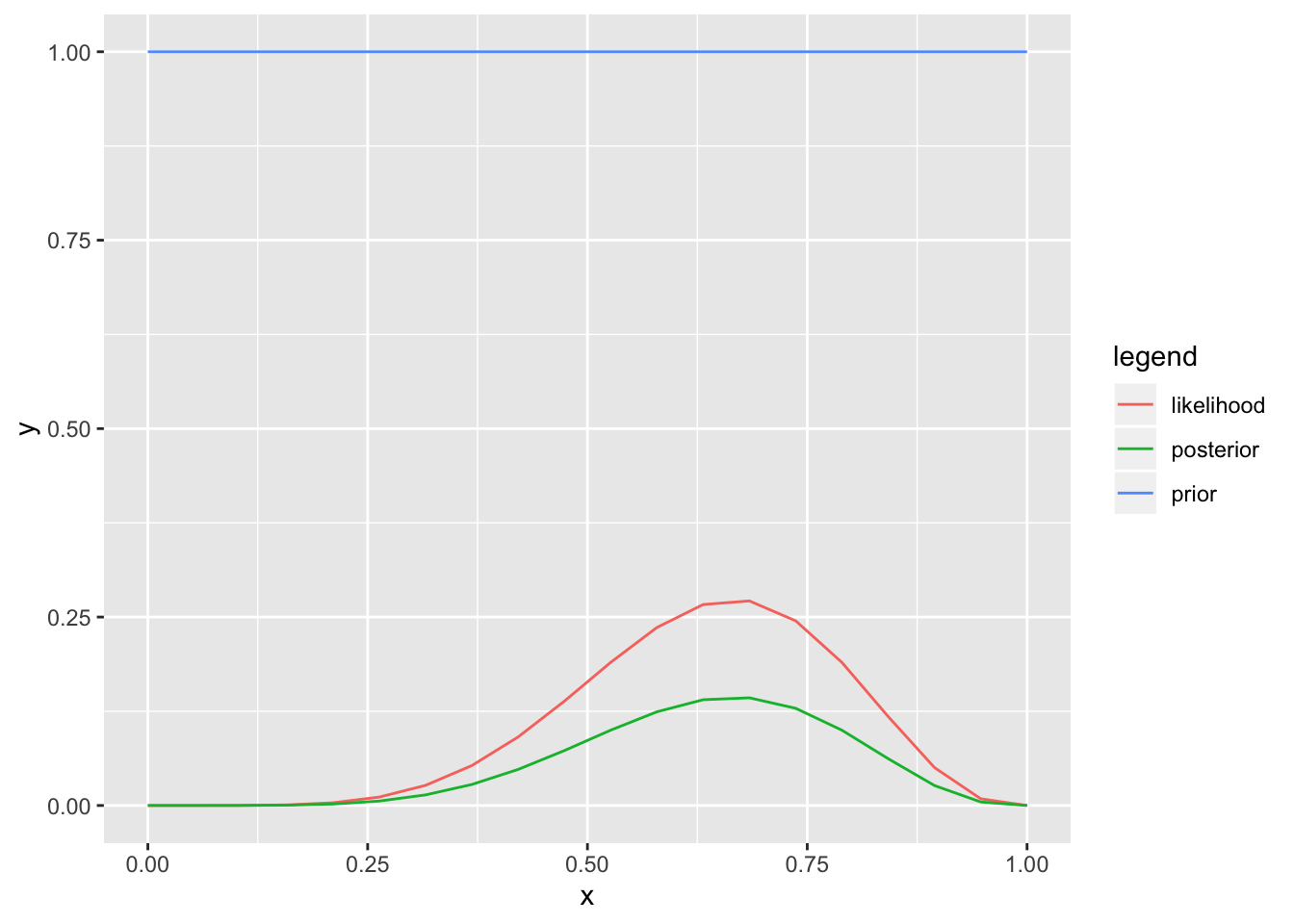

Nüüd on meil posterioorne tõenäosusfunktsioon, mis summeerub 1-le ja mis sisaldab kogu meie teadmist suremuse kohta.

Alati on kasulik plottida kõik kolm funktsiooni (tõepära, prior ja posteerior).

Kui n = 1

Bayes on lahe sest tema hinnangud väiksele N-le on loogiliselt sama pädevad kui suurele N-le. See ei ole nii klassikalises sageduslikus statistikas, kus paljud testid on välja töötatud N = Inf eeldusel ja töötavad halvasti väikeste valimitega.

Hea küll, me arvutame jälle suremust.

Bayes töötab andmepunkti kaupa (see et me talle ennist kõik andmed korraga ette andsime, on puhtalt mugavuse pärast).

# Define grid
x <- seq(from = 0, to = 1, length.out = 20)

# Define prior
prior <- rep(1, 20)

# Compute likelihood at each value in grid
likelihood <- dbinom(1, size = 1, prob = x)
posterior <- likelihood * prior / sum(likelihood * prior)

ggplot(data=NULL)+
  geom_line(aes(x, posterior), color= "blue")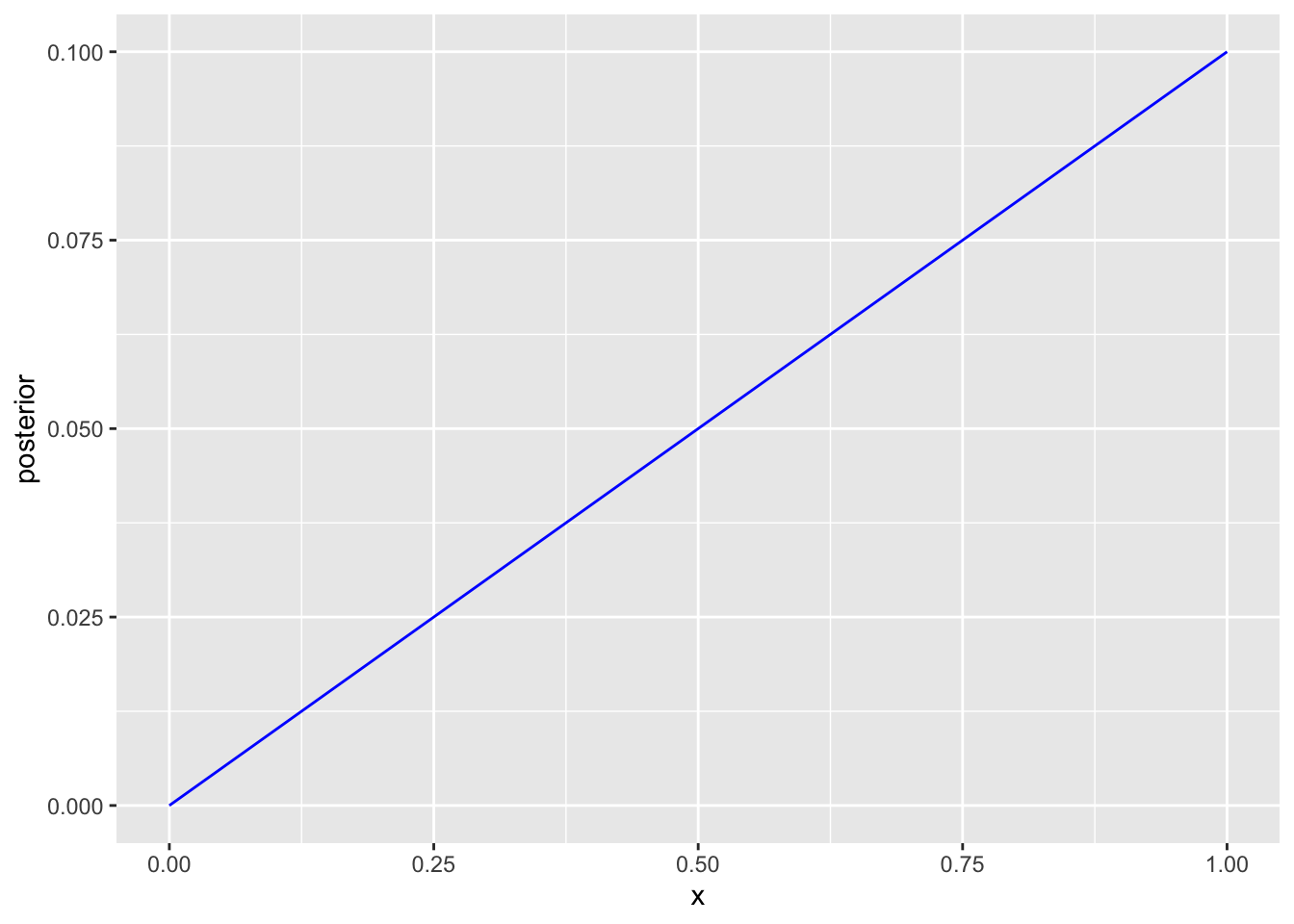

Joonis 13.1: N=1, esimene patsient suri.

Esimene patsient suri - 0 mortaalsus ei ole enam loogiliselt võimalik (välja arvatud siis kui prior selle koha peal = 0) ja mortaalsus 100% on andmetega (tegelikult andmega) parimini kooskõlas. Posteerior on nulli ja 100% vahel sirge sest vähene sissepandud informatsioon lihtsalt ei võimalda enamat.

x <- seq(from = 0, to = 1, length.out = 20)
# Define prior
prior <- posterior

# Compute likelihood at each value in grid
likelihood <- dbinom(1 , size = 1, prob = x)
posterior1 <- likelihood * prior / sum(likelihood * prior)

ggplot(data=NULL)+
  geom_line(aes(x, prior))+
  geom_line(aes(x, posterior1), color="blue")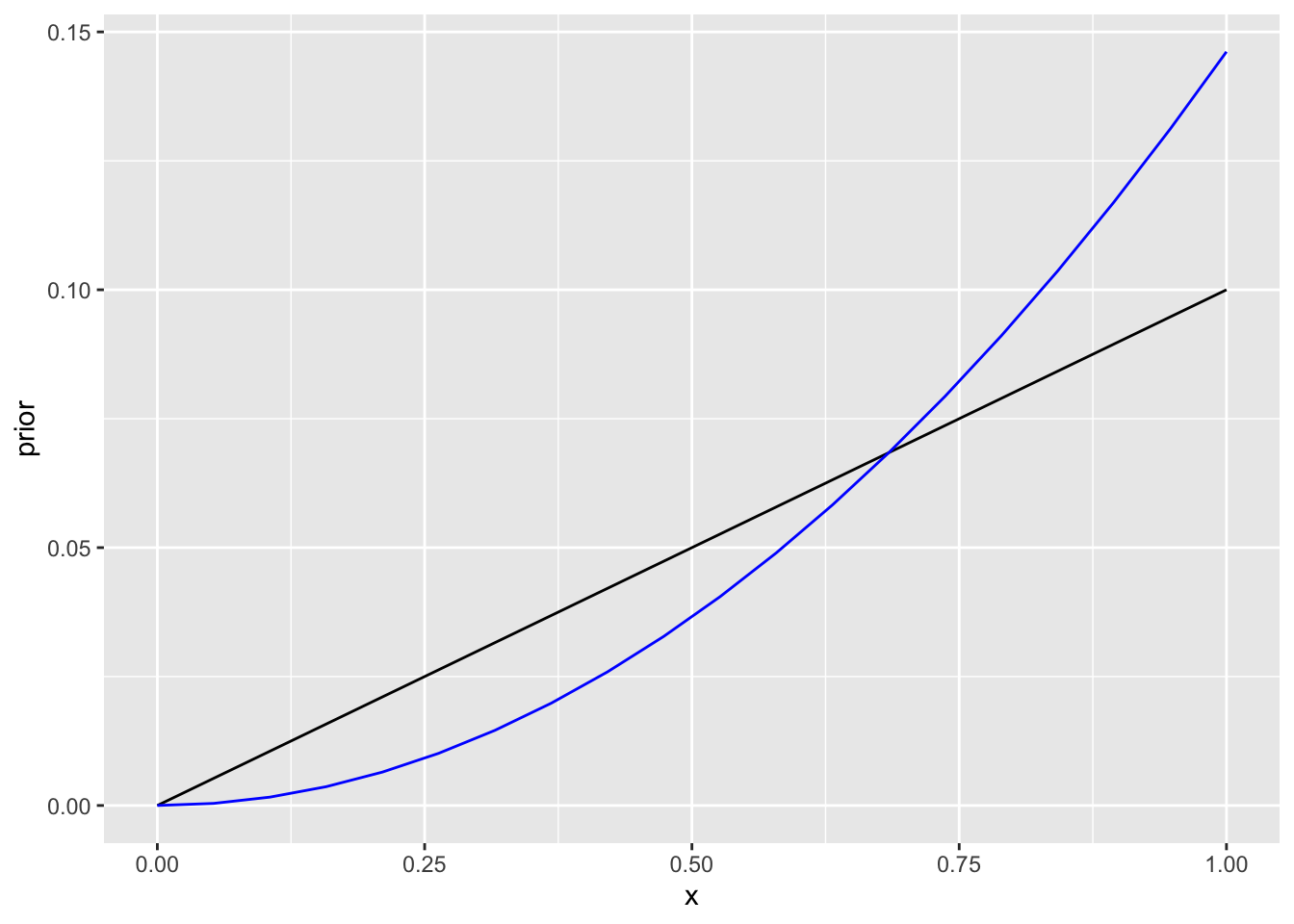

Joonis 13.2: N=2, teine patsient suri.

Teine patsient suri. Nüüd ei ole 0 ja 1 vahel enam sirge posteerior. Posteerior on kaldu 100 protsendi poole, mis on ikka kõige tõenäolisem väärtus.

x <- seq(from = 0, to = 1, length.out = 20)
# Define prior
prior <- posterior1

# Compute likelihood at each value in grid
likelihood <- dbinom(0, size = 1, prob = x)

# Compute product of likelihood and prior
posterior2 <- likelihood * prior / sum(likelihood * prior)

ggplot(data=NULL)+
  geom_line(aes(x, prior))+
  geom_line(aes(x, posterior2), color="blue")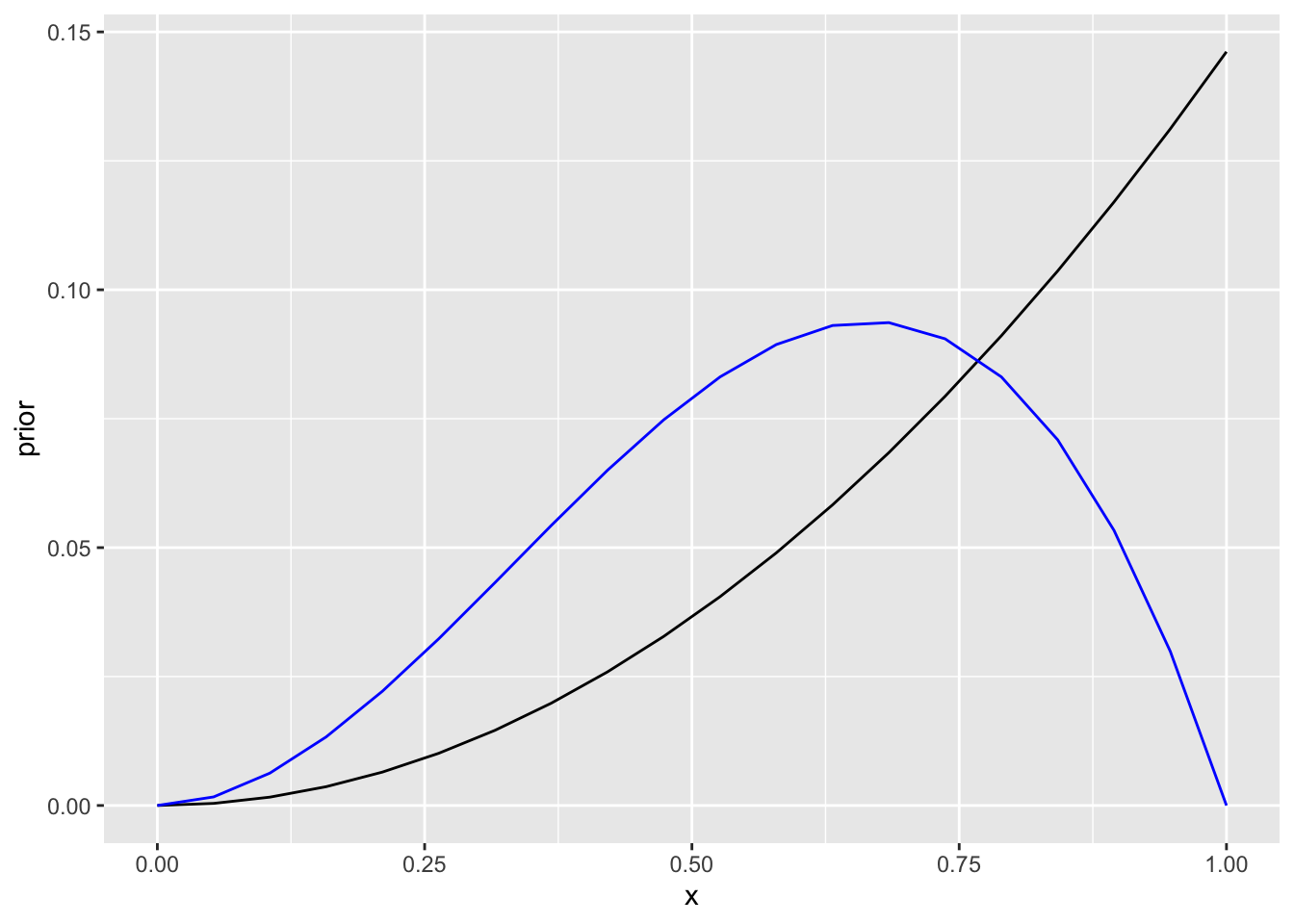

Joonis 13.3: N=3, kolmas patsient jäi ellu.

Kolmas patsient jäi ellu - 0 ja 100% mortaalsus on seega võimaluste nimekirjast maas ning suremus on ikka kaldu valimi keskmise poole (75%).

Teeme sedasama prioriga, mis ei ole tasane. See illustreerib tõsiasja, et kui N on väike siis domineerib prior posteerior jaotust. (Suure N korral on vastupidi, priori kuju on sageli vähetähtis.)

x <- seq(from = 0, to = 1, length.out = 20)
# Define prior
prior <- c(seq(0.01, 0.1, length.out = 10), seq(0.1, 0.01, length.out = 10))

# Compute likelihood at each value in grid
likelihood <- dbinom(1, size = 1 , prob = x)
posterior <- likelihood * prior / sum(likelihood * prior)

ggplot(data=NULL)+
  geom_line(aes(x, prior))+
  geom_line(aes(x, likelihood), color="red")+
  geom_line(aes(x, posterior), color="blue")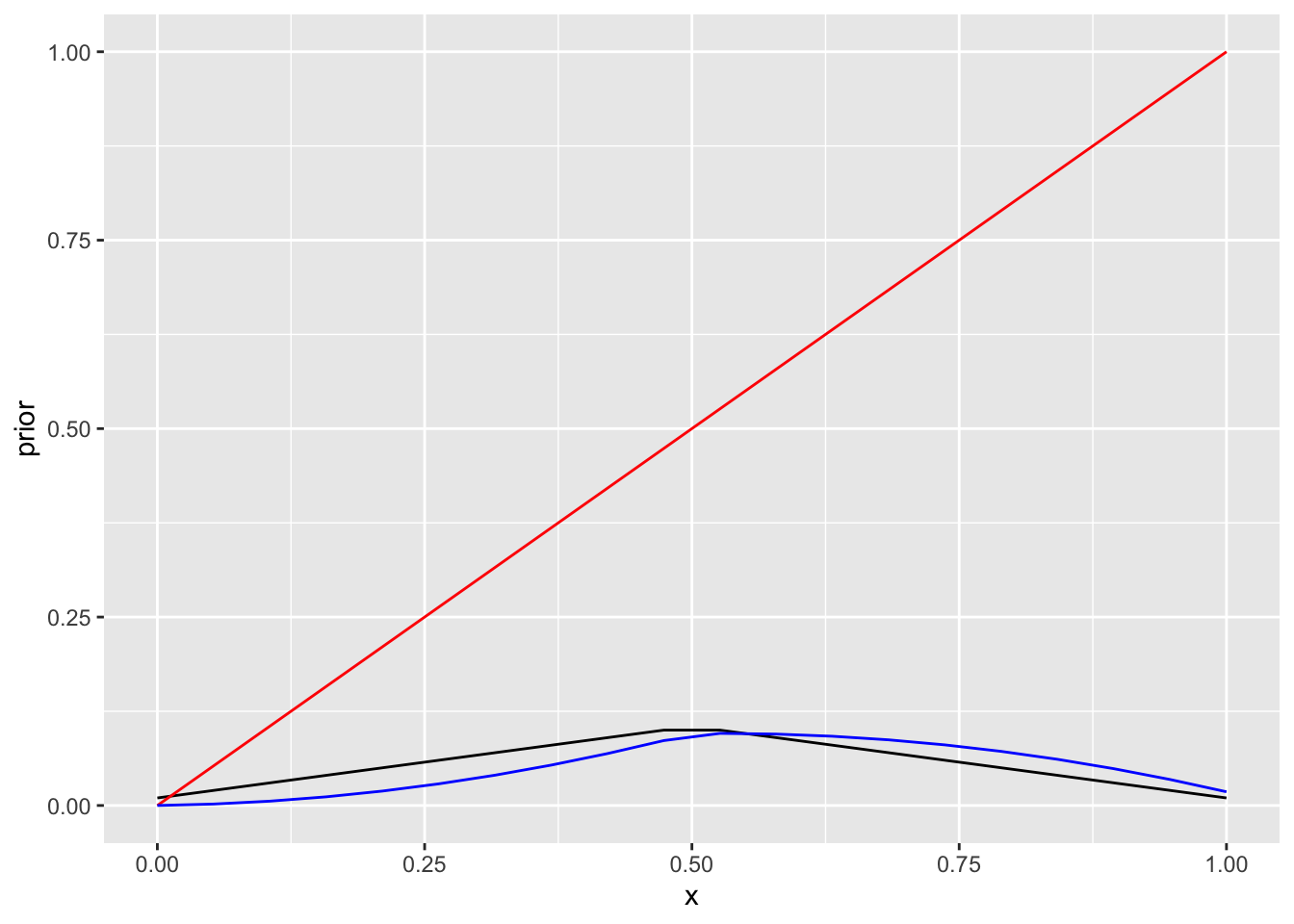

1. patsient suri

# Define prior
prior <- posterior

# Compute likelihood at each value in grid
likelihood <- dbinom(2, size = 2, prob = x)

# Compute product of likelihood and prior
posterior1 <- likelihood * prior / sum(likelihood * prior)

ggplot(data=NULL)+
  geom_line(aes(x, prior))+
  geom_line(aes(x, likelihood), color="red")+
  geom_line(aes(x, posterior1), color="blue")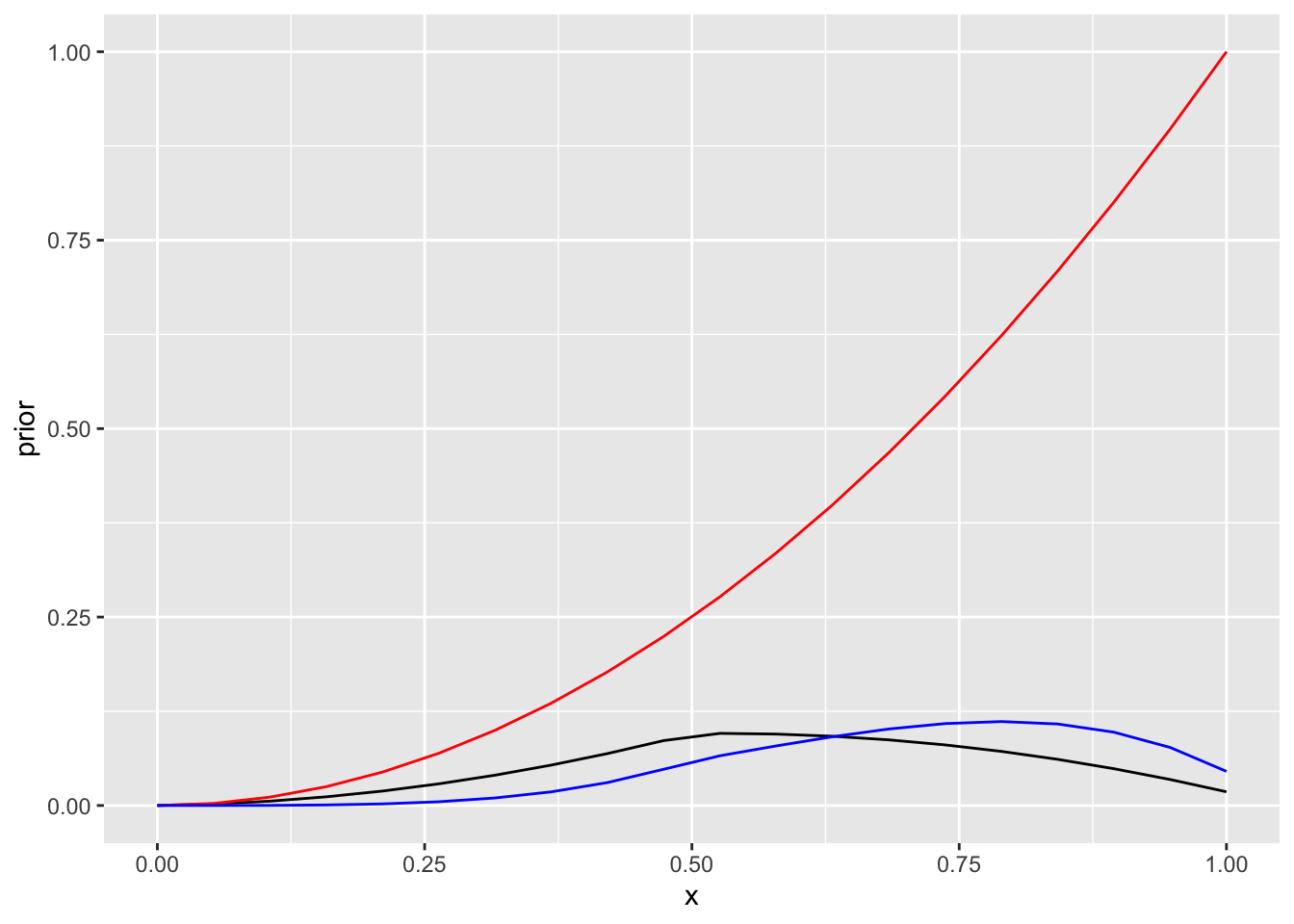

Joonis 13.4: N=2 informatiivse prioriga.

Teine patsient suri.

# Define prior
prior2 <- posterior1

# Compute likelihood at each value in grid
likelihood <- dbinom(2, size = 3, prob = x)

# Compute product of likelihood and prior
posterior2 <- likelihood * prior2 / sum(likelihood * prior2)

ggplot(data=NULL)+
  geom_line(aes(x, prior2))+
  geom_line(aes(x, likelihood), color="red")+
  geom_line(aes(x, posterior2), color="blue")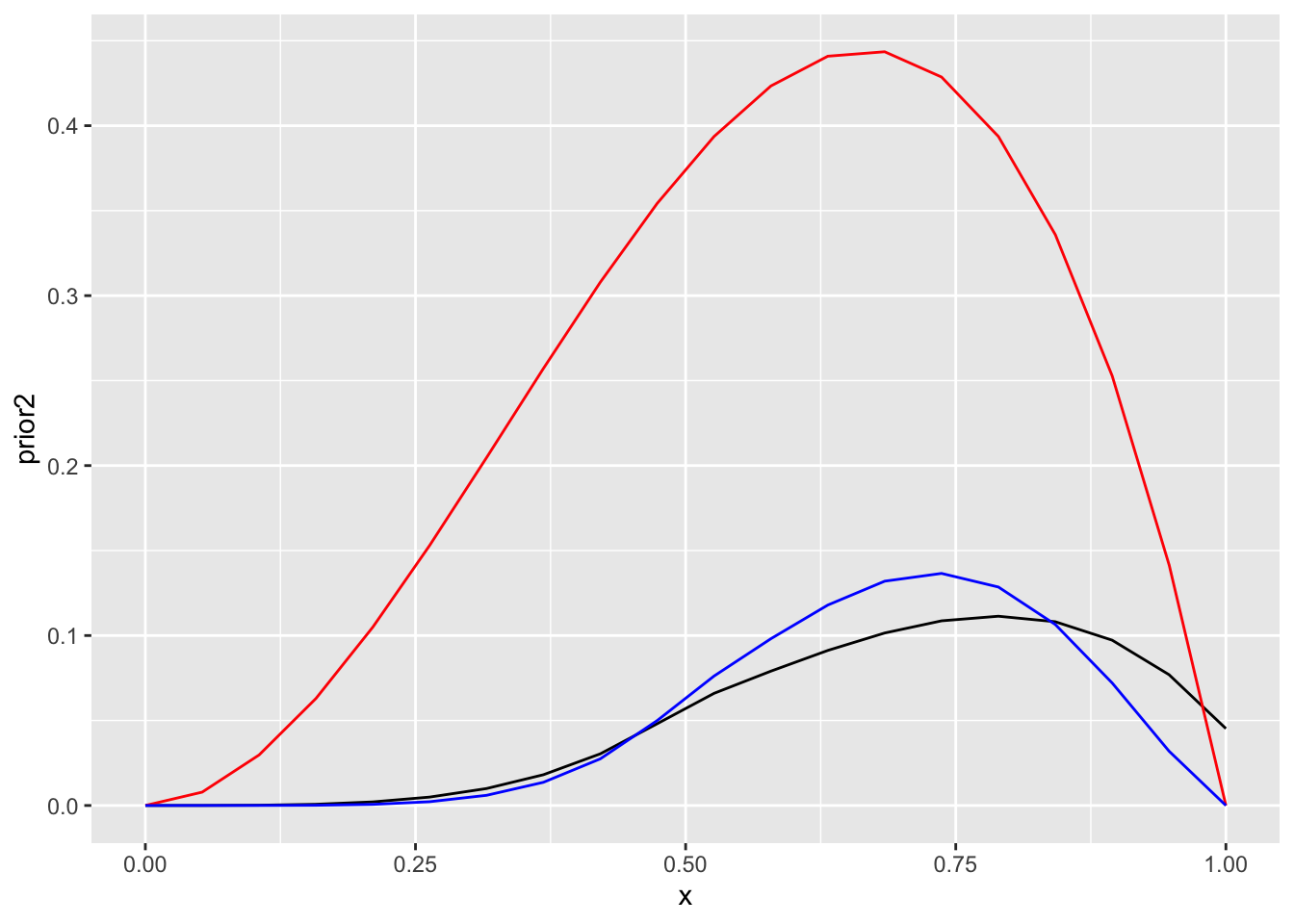

Joonis 13.5: N=3 informatiivse prioriga.

Kolmas patsient jäi ellu. Nüüd on posteeriori tipp mitte 75% juures nagu ennist, vaid kuskil 50% juures — tänu priorile.