9 EDA — eksploratoorne andmeanalüüs
library(tidyverse)
library(corrgram)
library(psych)
library(skimr)Kui ühenumbriline andmete summeerimine täidab eelkõige kokkuvõtliku kommunikatsiooni eesmärki, siis EDA on suunatud teadlasele endale. EDA eesmärk on andmeid eelkõige graafiliselt vaadata, et saada aimu 1) andmete kvaliteedist ja 2) lasta andmetel kõneleda “sellisena nagu nad on” ja sugereerida uudseid teaduslikke hüpoteese. Neid hüpoteese peaks siis testima formaalse statistilise analüüsi abil (ptk järeldav statistika). Näiteid erinevate graafiliste lahenduste kohta vt graafika peatükist.
EDA: mida rohkem graafikuid, seda rohkem võimalusi uute mõtete tekkeks!
EDA on rohkem kunst kui teadus selles mõttes, et teil on suur vabadus küsida selle abil erinevaid küsimusi oma andmete kohta. Ja seda nii tehnilisest aspektist lähtuvalt (milline on minu andmete kvaliteet?), kui teaduslikke küsimusi küsides (kas muutuja A võiks põhjustada muutusi muutujas B?).
Mõned üldised soovitused võib siiski anda.
- alusta analüüsi tasemest, kus andmed on kõige inforikkamad — toorandmete plottimisest punktidena. Kui andmehulk ei ole väga massiivne, näitab see hästi nii andmete kvaliteeti, kui ka võimalikke sõltuvussuhteid erinevate muutujate vahel.
Millised korrelatsioonid võiksid andmetes esineda?
corrgram(iris,
order = TRUE,
lower.panel = panel.pts,
upper.panel = panel.ellipse,
diag.panel = panel.density,
main = "Correlogram of Iris dataset")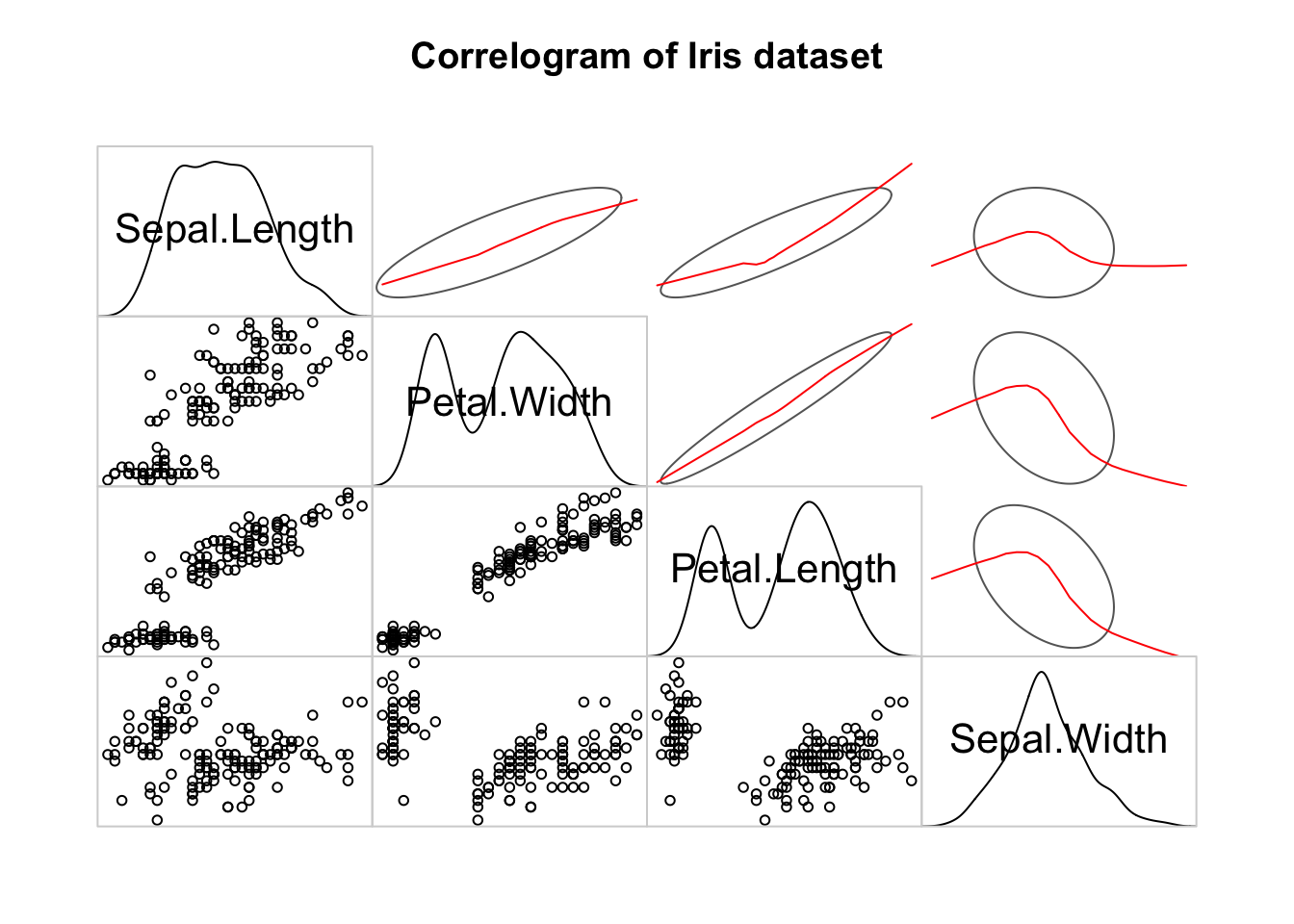
Joonis 9.1: Korrelatstioonimaatriks joonisena.
- vaata andmeid numbrilise kokkuvõttena.
psych::describe(iris)
#> vars n mean sd median trimmed mad min max range skew
#> Sepal.Length 1 150 5.84 0.83 5.80 5.81 1.04 4.3 7.9 3.6 0.31
#> Sepal.Width 2 150 3.06 0.44 3.00 3.04 0.44 2.0 4.4 2.4 0.31
#> Petal.Length 3 150 3.76 1.77 4.35 3.76 1.85 1.0 6.9 5.9 -0.27
#> Petal.Width 4 150 1.20 0.76 1.30 1.18 1.04 0.1 2.5 2.4 -0.10
#> Species* 5 150 2.00 0.82 2.00 2.00 1.48 1.0 3.0 2.0 0.00
#> kurtosis se
#> Sepal.Length -0.61 0.07
#> Sepal.Width 0.14 0.04
#> Petal.Length -1.42 0.14
#> Petal.Width -1.36 0.06
#> Species* -1.52 0.07skimr::skim(iris)
#> Skim summary statistics
#> n obs: 150
#> n variables: 5
#>
#> ── Variable type:factor ────────────────────────────────────────────────────────────────────────
#> variable missing complete n n_unique top_counts
#> Species 0 150 150 3 set: 50, ver: 50, vir: 50, NA: 0
#> ordered
#> FALSE
#>
#> ── Variable type:numeric ───────────────────────────────────────────────────────────────────────
#> variable missing complete n mean sd p0 p25 p50 p75 p100
#> Petal.Length 0 150 150 3.76 1.77 1 1.6 4.35 5.1 6.9
#> Petal.Width 0 150 150 1.2 0.76 0.1 0.3 1.3 1.8 2.5
#> Sepal.Length 0 150 150 5.84 0.83 4.3 5.1 5.8 6.4 7.9
#> Sepal.Width 0 150 150 3.06 0.44 2 2.8 3 3.3 4.4Siin pööra kindlasti tähelepanu tulpadele min ja max, mis annavad kiire võimalusi outliereid ära tunda. Kontrolli, kas andmete keskmised (mediaan, mean ja trimmed mean) on üksteisele piisavalt lähedal — kui ei ole, siis on andmete jaotus pika õlaga, ja kindlasti mitte normaalne.
Kontrolli, kas erinevate muutujate keskväärtused ja hälbed on teaduslikus mõttes usutavas vahemikus.
Ära unusta, et ka väga väike standardhälve võib tähendada, et teie valim ei peegelda bioloogilist varieeruvust populatsioonis, mis teile teaduslikku huvi pakub.
NB! selles psych::describe() funktsiooni väljundis on mad läbi korrutatud konstandiga 1.4826, mis toob selle väärtuse lähemale sd-le.
Seega on mad siin sd robustne analoog — kui mad on palju väiksem sd-st, siis on karta, et muutujas on outliereid.
kontrolli NA-de esinemist oma andmetes VIM paketi abil või käsitsi (vt esimene ptk). Kontrolli, et NA-d ei oleks tähistatud mingil muul viisil (näiteks 0-i või mõne muu numbriga). Kui vaja, rekodeeri NAd. Mõtle selle peale, millised protsessid looduses võiksid genreerida puuduvaid andmeid. Kui NA-d ei jaotu andmetes juhuslikult, võib olla hea mõte andmeid imputeerida (vt hilisemaid ptk, bayesiaanlik imputeerimine). Näiteks, kui ravimiuuringust kukuvad eeskätt välja patsiendid, kellel ravim ei tööta, on ilmselt halb mõte nende patsientide andmed lihtsalt uuringust välja vistata (muidugi, kui te ei esinda kasumit taotleva ettevõtte huve). Kui NA-d jaotuvad juhuslikult, mõtle sellele, kas sa tahad NA-dega read tabelist välja visata, või hoopis osad muutujad, mis sisaldavad liiga palju NA-sid, või mitte midagi välja vistata. NB! NA-dega andmed ei sobi hästi regresiooniks.
Kui andmeid on nii palju, et üksikute andmepunktide vaatlemine paneb pea valutama, siis järgmine informatiivsuse tase on histogramm.
kui tahame kõrvuti vaadata paljude erinevate muutujate varieeruvust ja keskväärtusi, siis on head valikud joyplot, violin plot, ja vähem hea valik (sest ta kaotab andmetest rohkem infot) on boxplot. Kui meil on vaid 2-4 jaotust, mida võrrelda, siis saab mängida histogramme facetisse või üksteise otsa pannes (vt ptk graphics).
Tulpdiagramm on hea valik siis, kui tahate kõrvuti näidata proportsioonide erinevust. Näiteks, kui meil on 3 liiki kalu, millest igas on erinevas proporstioonis parasiidid, võime joonistada 3 tulpa, millest igas on näidatud ühe kalaliigi parasiitide omavaheline proportsioon.
Tulpdiagramm on hädaga pooleks kasutuskõlblik, kui iga muutuja kohta on vaid üks number, mida plottida. Kuigi, siin on meil parem võimalus — Cleveland plot. Olukorras, kus te tahate plottida valimi keskväärtust ja usalduspiire või varieeruvusnäitajat (sd, mad), on olemas selgelt paremad meetodid kui tulpdiagramm. Samas, ehki tulpdiagrammide kasutamine teaduskirjanduses on pikas langustrendis, kasutatakse neid ikkagi liiga palju just sellel viisil.
Ära piirdu muutuja tasemel varieeruvuse plottimisega. Teaduslikult on sageli huvitavam mimte muutuja koosvarieerumine. Järgmistes peatükkides modelleerime seda formaalselt regresioonanalüüsis aga alati tasub alustada lihtsatest plottidest. Scatterplot on lihtne viis kovarieeruvuse vaatamiseks.
Kui erinevad muutujad on mõõdetud erinevates skaalades (ühikutes), siis võib nende koosvarieeruvust olla kergem võrrelda, kui nad eelnevalt normaliseerida (kõigi muutujate keskväärtus = 0, aga varieeruvus jääb algsesse skaalasse) või standardiseerida (kõik keskväärtused = 0-ga ja sd-d = 1-ga). Normaliseerimine: arvuta igale valimi väärtusele:
mean(x) - x; standardiseerimine:(mean(x) - x) / sd(x).Visualiseeringu valik sõltub valimi suurusest. Väikse valimi korral (N<10) boxploti, histogrammi vms kasutamine on lihtsalt rumal. Ära mängi lolli ja ploti parem punkti kaupa.
N < 20 - ploti iga andmepunkt eraldi (
stripchart(),plot()) ja keskmine või mediaan.20 > N > 100:
geom_dotplot()histogrammi vaatesN > 100:
geom_histogram(),geom_density()— nende abil saab ka 2 kuni 6 jaotust võrreldaMitme jaotuse kõrvuti vaatamiseks, kui N > 15:
geom_boxplot(), orgeom_violin(),geom_joy()
- Nii saab plottida multiplikatiivse sd:
#> Warning: Ignoring unknown parameters: bins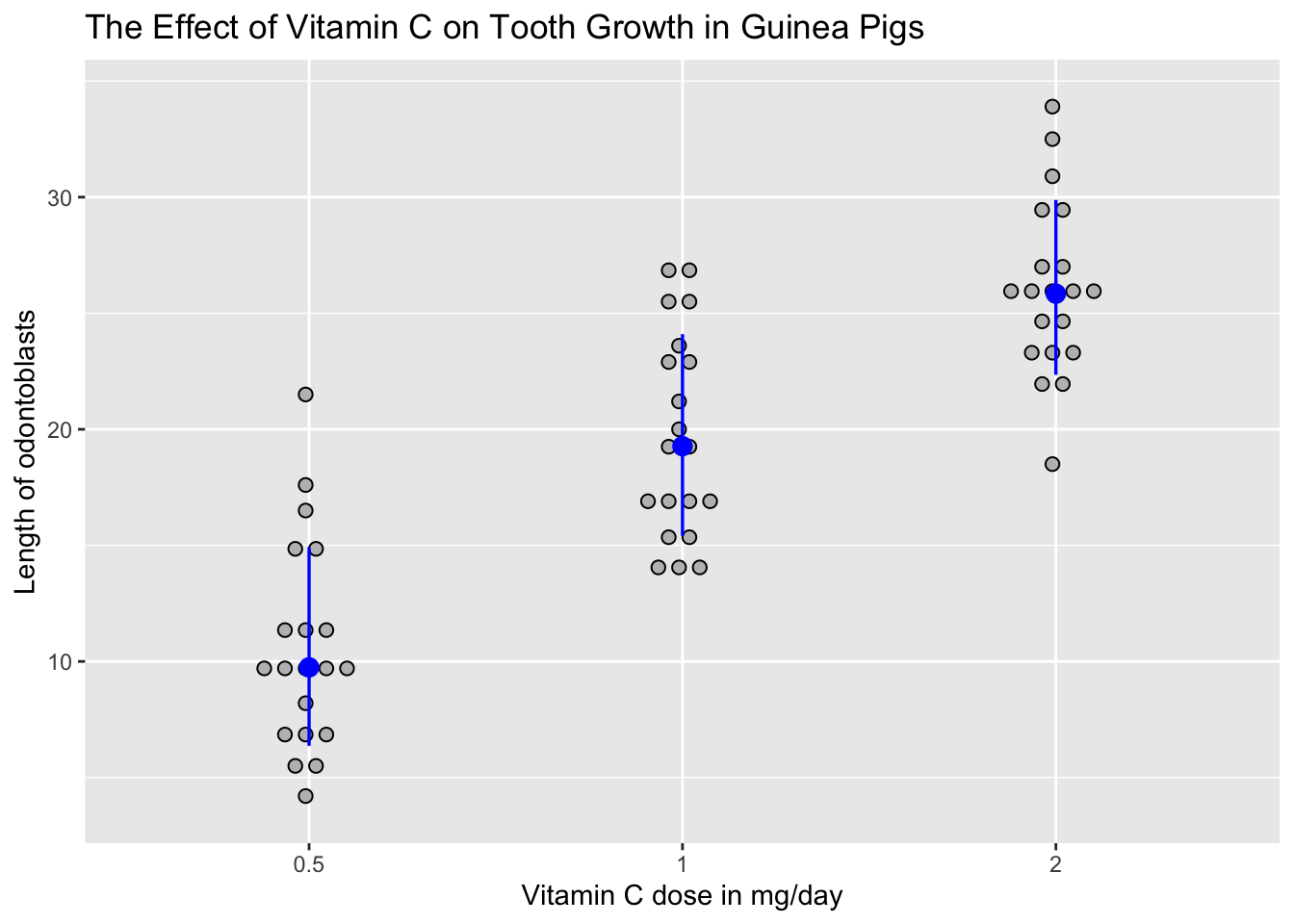
Joonis 9.2: Multiplikatiivse sd joonistamine.
9.1 EDA kokkuvõte
Andmepunktide plottimine säilitab maksimaalselt andmetes olevat infot (nii kasulikku infot kui müra). Aitab leida outliereid (valesti sisestatud andmeid, valesti mõõdetud proove jms). Kui valim on väiksem kui 20, piisab täiesti üksikute andmepunktide plotist koos mediaaniga. Dot-plot ruulib.
Histogramm – kõigepealt mõõtskaala ja seejärel andmed jagatakse võrdse laiusega binnidesse ja plotitakse binnide kõrgused. Bin, kuhu läks 20 andmepunkti on 2X kõrgem kui bin, kuhu läks 10 andmepunkti. Samas, bini laius/ulatus mõõteskaalal pole teile ette antud – ja sellest võib sõltuda histogrammi kuju. Seega on soovitav proovida erinevaid bini laiusi ja võrrelda saadud histogramme. Histogramm sisaldab vähem infot kui dot plot, aga võimaldab paremini tabada seaduspärasid & andmejaotust & outliereid suurte andmekoguste korral.
Density plot. Silutud versioon histogrammist, mis kaotab infot aga toob vahest välja signaali müra arvel. Density plotte on hea kõrvuti vaadelda joy ploti abil.
Box-plot –- sisaldab vähem infot kui histogramm, kuid neid on lihtsam kõrvuti võrrelda. Levinuim variant (kuid kahjuks mitte ainus) on Tukey box-plot – mediaan (joon), 50% IQR (box) ja 1,5x IQR (vuntsid), pluss outlierid eraldi punktidena.
Violin plot –- informatiivsuselt box-ploti ja histogrammi vahepeal – sobib paljude jaotuste kõrvuti võrdlemiseks.
Line plot –- kasuta ainult siis kui nii X kui Y teljele on kantud pidev väärtus (pikkus, kaal, kontsentratsioon, aeg jms). Ära kasuta, kui teljele kantud punktide vahel ei ole looduses mõtet omavaid pidevaid väärtusi (näiteks X teljel on katse ja kontroll või erinevad valgumutatsioonid, mille aktiivsust on mõõdetud).
Tulpdiagramm – Suhete võrdlemine (bar).
Cleveland plot on hea countide võrdlemiseks. Kui Cleveland plot mingil põhjusel ei sobi, kasuta tupldiagrammi.
Pie chart on proportsioonide vaatamiseks enam-vähem kõlblik ainult siis, kui teil pole vaja võrrelda proportsioone erinevates objektides. Kõik graafikud, kus lugeja peab võrdlema pindalasid, on inimmõistusele petlikud — lugeja alahindab süstemaatiliselt erinevuste suurusi! Selle pärast on proportsioonide võrdlemiseks palju parem tulpdiagramm, kus võrreldavad tulbad on ühekõrgused.
Informatsiooni hulk kahanevalt: iga andmepunkt plotitud —> histogramm —> density plot & violin plot —> box plot —> tulpdiagramm standardhälvetega —> cleveland plot (ilma veapiirideta)