4 Lineaarsed mudelid

library(tidyverse)
library(ggthemes)
library(broom)
library(modelr)
library(viridis)

4.1 Sirge võrrand

Oletame, et me mõõtsime N inimese pikkuse cm-s ja kaalu kg-s ning meid huvitab, kuidas inimeste pikkus sõltub nende kaalust. Lihtsaim mudel pikkuse sõltuvusest kaalust on pikkus = kaal (formaliseeritult: y = x) ja see mudel ennustab, et kui Juhani kaal = 80 kg, siis Juhan on 80 cm pikkune. Siin on pikkus muutuja, mille väärtust ennustatakse (y) ja kaal muutuja x, mille väärtuste põhjal ennustatakse pikkusi. Muidugi, sama hästi võiksime ennustada kaalu pikkuste põhjal, ja kumma ennustuse valime sõltub siinkohal eeskätt meie teaduslikest huvidest.

Veelgi enam, sama mudel ennustab, et kui Juhani kaal = 80 tonni, siis on Juhan samuti 80 cm pikkune (eeldusel, et me avaldame x muutuja tonnides ja y muutuja sentimeetrites). Seega, mudeli ennustuse täpsus sõltub ühikutest, milles me andmed mudelisse sisse anname.

#Genereerime andmed: x = pikkus ja y = kaal:
x <- 0:100
y <- x

Selle mudeli saame graafiliselt kujutada nii:

plot(y ~ x, 
     type = "l", 
     xlab = "Weight in kg", 
     ylab = "Heigth in cm", 
     main = bquote(y == x))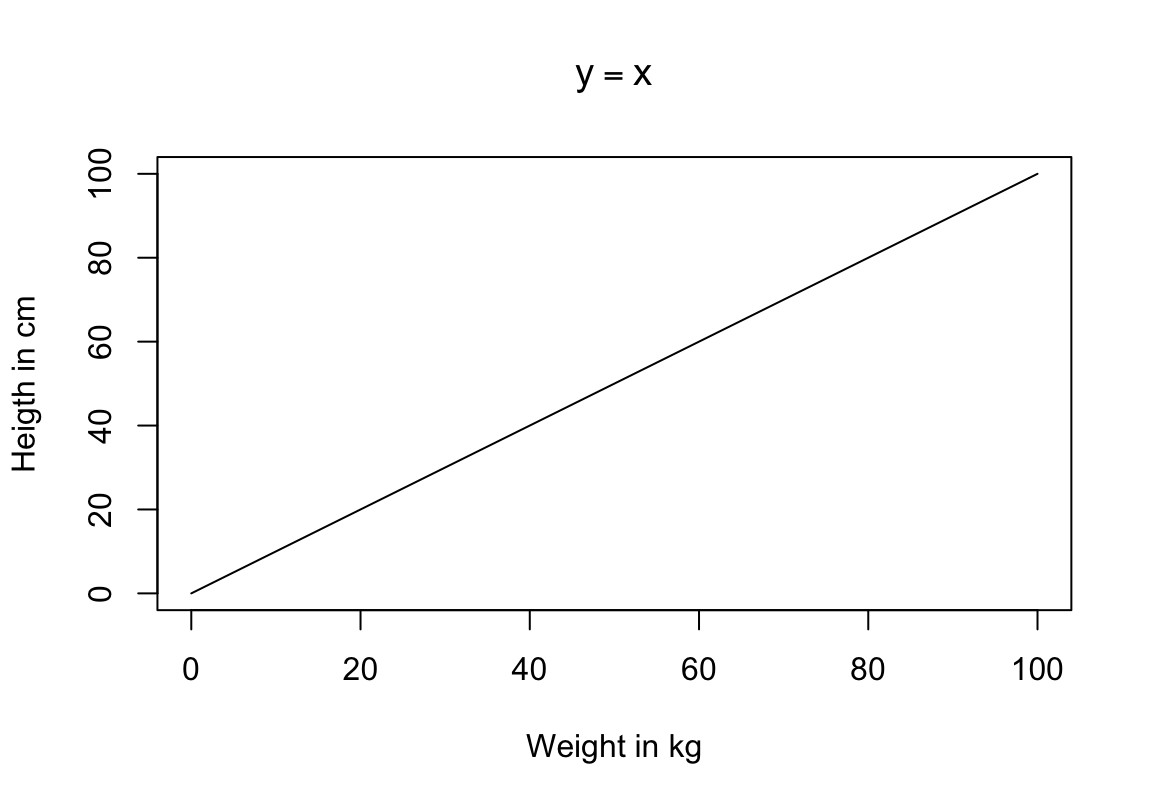

Joonis 4.1: Lihtne mudel y ~ x, mille lõikepunkt = 0 ja tõus = 1.

Üldistatult, mudeli keeles tähistame me seda muutujat, mille väärtusi me ennustame, Y-ga ja seda muutujat, mille väärtuse põhjal me ennustame, X-ga.

Sirge mudeli lihtsaim matemaatiline formalism on Y = X. See on äärmiselt jäik mudel: sirge, mille asukoht on rangelt fikseeritud. Sirge lõikab y telge alati 0-s (mudeli keeles: sirge intercept ehk lõikepunkt Y teljel = 0) ja tema tõusunurk saab olla ainult 45 kraadi (mudeli keeles slope ehk tõus = 1). Selle mudeli jäikus tuleneb sellest, et temas ei ole parameetreid, mille väärtusi me saaksime vabalt muuta ehk tuunida.

Mis juhtub, kui me lisame mudelisse konstandi, mille liidame x-i väärtustele?

\[y = a + x\]

See konstant on mudeli parameeter, mille väärtuse võime vabalt valida. Järgnevalt anname talle väärtuse 30 (ilma konkreetse põhjuseta).

x <- 0:100 
a <- 30
y <- a + x

plot(y ~ x, xlim = c(0, 100), ylim = c(0, 150), type = "l",
     main = bquote(y == a + x))
abline(c(0, 1), lty = 2)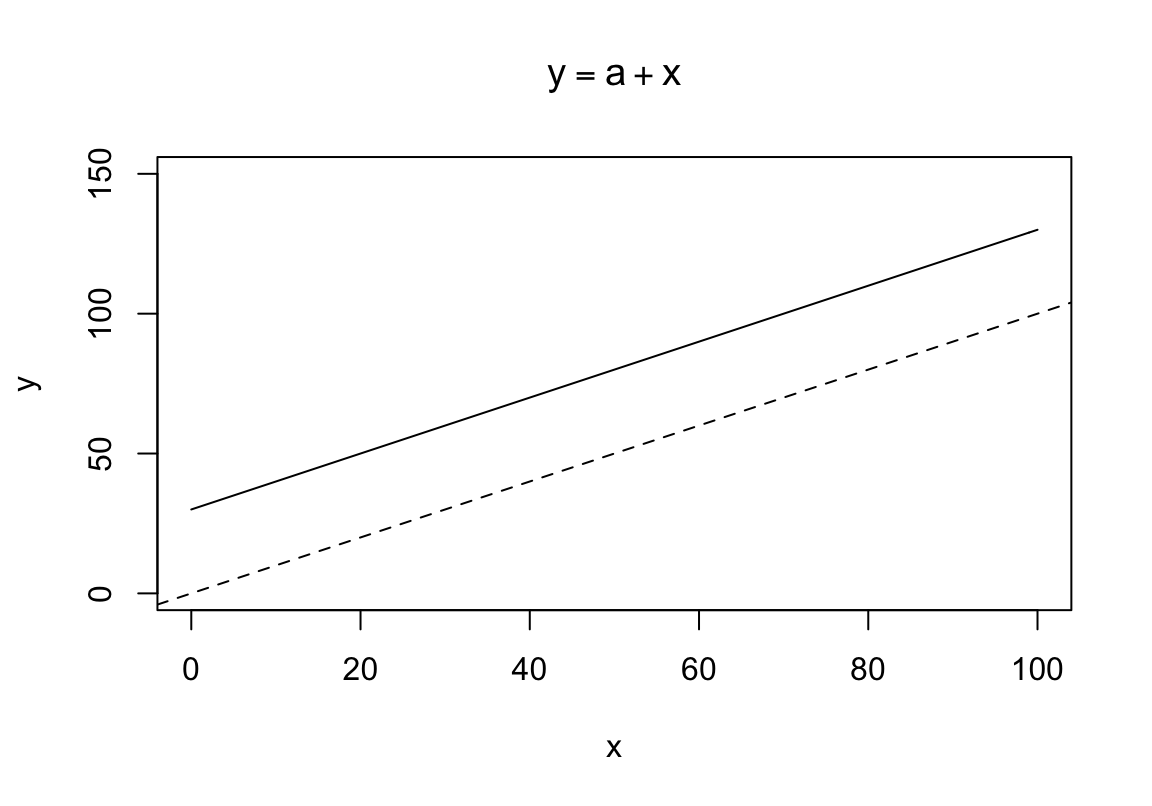

Joonis 4.2: Lineaarne mudel, mille lõikepunkt = 30 ja tõus = 1. Katkendjoon, lõikepunkt = 0. Pidevjoon, lõikepunkt = 30

Meie konstant a määrab \(y\) väärtuse, kui \(x = 0\), ehk sirge lõikepunkti \(y\) teljel. Teisisõnu, a = mudeli lõikepunkt (intercept).

Mis juhtub, kui me mitte ei liida, vaid korrutame x-i konstandiga?

\[y = b \times x\]

Jällegi, me anname mudeli parameetrile b suvalise väärtuse, 3.

x <- 0:200
b <- 3
y <- b * x

plot(y ~ x, xlim = c(0, 100), ylim = c(0, 100), type = "l", main = bquote(y == b %*% x))
abline(c(0, 1), lty = 2)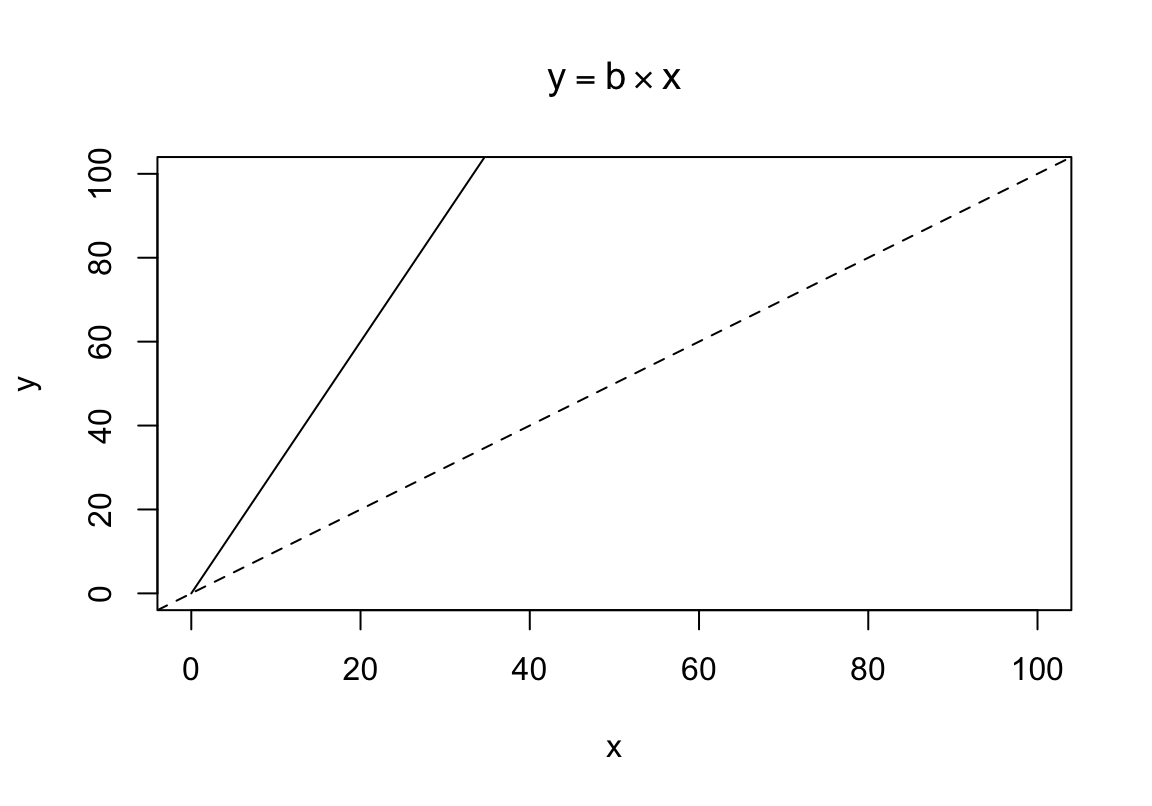

Joonis 4.3: Lineaarne mudel, mille lõikepunkt = 0 ja tõus = 3. Katkendjoon, tõus = 1. Pidevjoon, tõus = 3.

Nüüd muutub sirge tõusunurk, ehk kui palju me ootame y-t muutumas, kui x muutub näiteks ühe ühiku võrra. Kui b = 3, siis x-i tõustes ühe ühiku võrra suureneb y kolme ühiku võrra. Proovi järgi, mis juhtub, kui b = -3.

Selleks, et sirget kahes dimensioonis vabalt liigutada, piisab kui me kombineerime eelnevad näited ühte:

\[y = a + b \times x\]

Selleks lisame mudelisse kaks parameetrit, lõikepunkt (a) ja tõus (b). Kui \(a = 0\) ja \(b = 1\), saame me eelpool kirjeldatud mudeli \(y = x\). Kui \(a = 102\), siis sirge lõikab y-telge väärtusel 102. Kui \(b = 0.8\), siis x-i tõustes 1 ühiku võrra tõuseb y-i väärtus 0.8 ühiku võrra. Kui \(a = 100\) ja \(b = 0\), siis saame sirge, mis on paraleelne x-teljega ja lõikab y-telge väärtusel 100. Seega, teades a ja b väärtusi ning omistades x-le suvalise meid huvitava väärtuse, saab ennustada y-i keskmist väärtust sellel x-i väärtusel. Näiteks, olgu andmete vastu fititud mudel pikkus(cm) = 102 + 0.8 * kaal(kg) ehk

\[y = 102 + 0.8 \times x\]

Omistades nüüd kaalule väärtuse 80 kg, tuleb mudeli poolt ennustatud keskmine pikkus 102 + 0.8 * 80 = 166 cm. Iga kg lisakaalu ennustab mudeli kohaselt 0.8 cm võrra suuremat pikkust.

a <- 102
b <- 0.8
x <-  0:100 
y <-  a + b * x

plot(y ~ x, xlab = "Weight in kg", ylab = "Heigth in cm", ylim = c(50, 200), type = "l", main = bquote(y == 102 + 0.8 %*% x))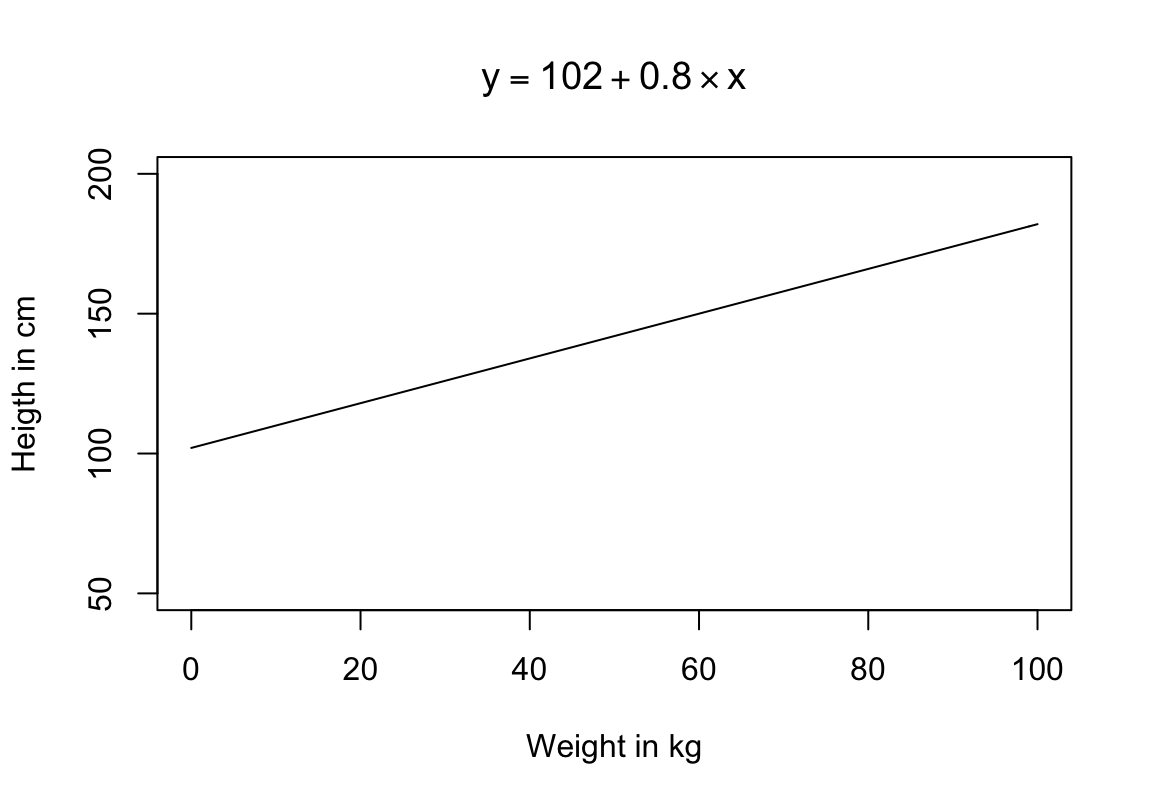

Joonis 4.4: Lineaarne mudel, millel on tuunitud nii lõikepunkt kui tõus.

See mudel ennustab, et 0 kaalu juures on pikku 102 cm, mis on rumal, aga mudelite puhul tavaline olukord. Sellel olukorral on mitmeid põhjusi:

Me tuunime mudelit andmete peal, mis ei sisalda 0-kaalu.
Meie valimiandmed ei peegelda täpselt inimpopulatsiooni.
Sirge mudel ei peegelda täpselt pikkuse-kaalu suhteid vahemikus, kus meil on reaalseid kaaluandmeid; ja ta teeb seda veelgi vähem seal, kus meil mõõdetud kaalusid ei ole.

Seega pole mõtet imestada, miks mudeli intercept meie üle irvitab.

Kahe parameetriga sirge mudel ongi see, mida me fitime kahedimensiooniliste andmetega.

Näiteks nii, kasutame R-i “iris” andmesetti:

# Fit a linear model and name the model object as m
m <- lm(Sepal.Length ~ Petal.Length, data = iris)

# Make a scatter plot, colored by the var called "Species"
# Draw the fitted regression line from m
augment(m, iris) %>% 
  ggplot(aes(Petal.Length, Sepal.Length, color = Species)) +
  geom_point() +
  geom_line(aes(y = .fitted), color = 1) +
  labs(title = "Sepal.Length ~ Petal.Length") +
  scale_color_viridis(discrete = TRUE)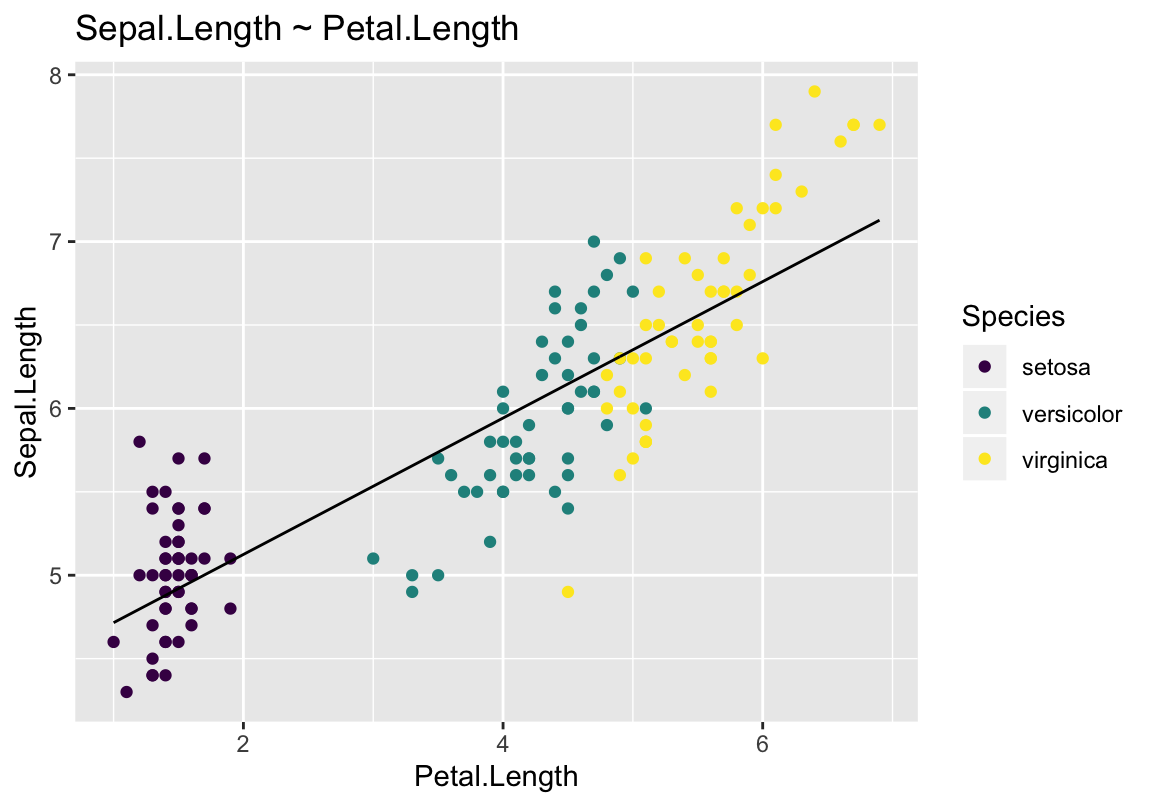

Joonis 4.5: Fititud mudel, kus muutuja Petal.Length järgi ennustatakse muutuja Sepal.Length väärtusi.

Mudeli fittimine tähendab siin lihtsalt, et sirge on 2D ruumi asetatud nii, et see oleks võimalikult lähedal kõikidele punktidele.

Oletame, et meil on n andmepunkti ja et me fitime neile sirge. Nüüd plotime fititud sirge koos punktidega ja tõmbame igast punktist mudelsirgeni joone, mis on paraleelne y-teljega. Seejärel mõõdame nende n joone pikkused. Olgu need pikkused a, b, … i. lm() funktsioon fitib sirge niimoodi, et summa \(a^2 + b^2 + ... + i^2\) oleks minimaalne. Seda kutsutakse vähimruutude meetodiks.

Mudeli koefitsientide väärtused saame kasutades funktsiooni coef():

coef(m)
#>  (Intercept) Petal.Length 
#>        4.307        0.409

Siin a = (Intercept) ja b = Petal.Length ehk 0.41.

4.2 Ennustus lineaarsest mudelist

Anname x-le rea väärtusi, et ennustada y keskmisi väärtusi nendel x-i väärtustel. Siin me ennustame y (Sepal_length) keskväärtusi erinevatel x-i (Petal_length) väärtustel, mitte individuaalseid Sepal_length väärtusi. Me kasutame selleks deterministlikku mudelit kujul Sepal_length = a + b*Petal_length. Hiljem õpime ka bayesiaanlike meetoditega individuaalseid Sepal_length-e ennustama.

Järgnev kood on sisuliselt sama, millega me üle-eelmisel plotil joonistasime mudeli y = a + bx. Me fikseerime mudeli koefitsiendid fititud irise mudeli omadega ja anname Petal_length muutujale 10 erinevat väärtust originaalse muutuja mõõtmisvahemikus. Aga sama hästi võiksime ekstrapoleerida ja küsida, mis on oodatav Sepal_length, kui Petal_length on 100 cm? Sellele küsimusele on ebareaalne vastus, aga mudel ei tea seda. Proovi, mis vastus tuleb.

## Genereerime uued andmed Petal.Length vahemikus
Petal_length <- seq(min(iris$Petal.Length), 
                    max(iris$Petal.Length), 
                    length.out = 10)
## Võtame mudeli koefitsendid
a <- coef(m)[1]
b <- coef(m)[2]
## Kasutades mudeli koefitsente genereerime Sepal_length väärtused
Sepal_length <-  a + b * Petal_length

plot(Sepal_length ~ Petal_length, type = "b")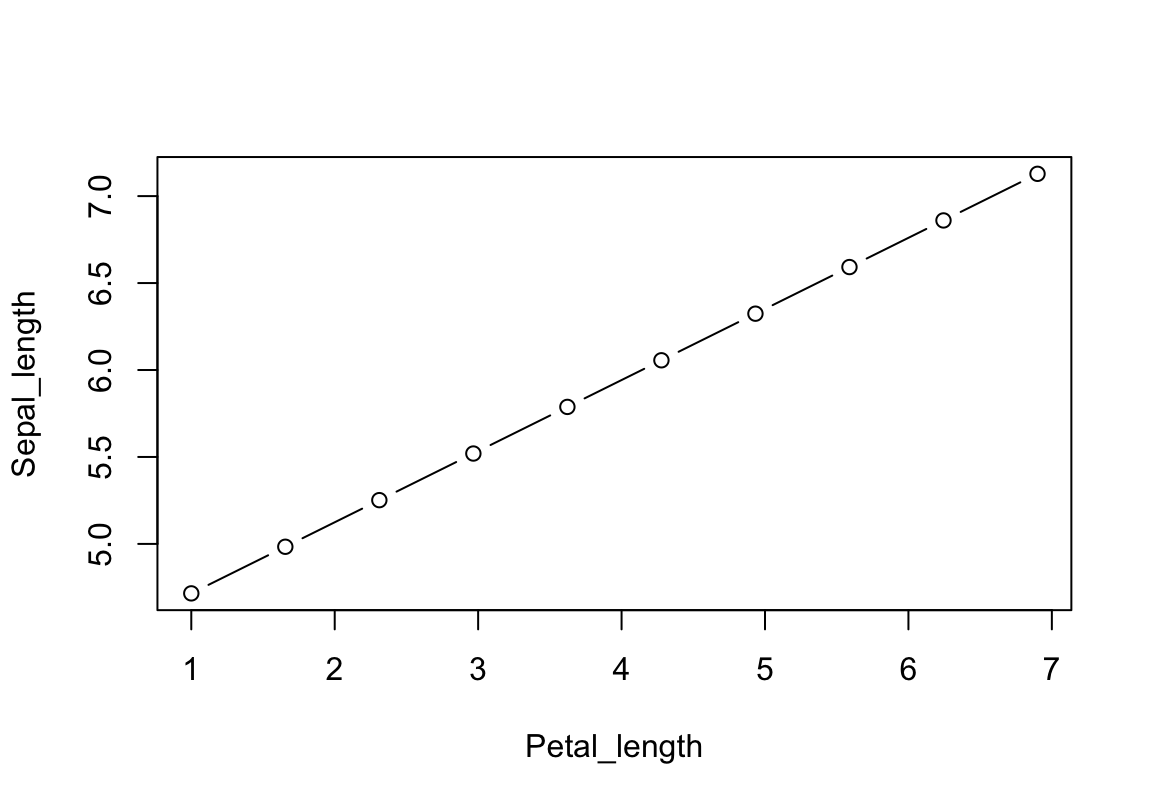

Joonis 4.6: Siin ennustasime kümme y väärtust x väärtuste põhjal..

Mudelist saab kahte tüüpi ennustusi: interpolatsioone (ennustus on samas skaalas, mis andmed, mille peal mudel fititi) ja ekstrapoleerimine (ennustus jääb väljaspoole andmeid). Sõltuvalt erialast me kas vaatame ekstrapoleerimisele viltu või leiame, et selline tegevus on otsesõnu keelatud.

Mudelist saab kahte tüüpi ennustusi: (1) saame ennustada Y keskmist väärtust X-i konkreetsel väärtusel ja (2) saame ennustada individuaalseid Y väärtusi X-i konkreetsel väärtusel. Viimase kohta vt ptk…

4.3 Neli mõistet

Mudelis \(y = a + bx\) on \(x\) ja \(y\) muutujad, ning \(a\) ja \(b\) on parameetrid. Muutujate väärtused fikseeritakse andmetega, parameetrid fititakse andmete põhjal. Fititud mudel valib kõikide võimalike seda tüüpi mudelite hulgast välja täpselt ühe unikaalse mudeli ja ennustab igale \(x\)-i väärtusele vastava kõige tõenäolisema \(y\) väärtuse (\(y\) keskväärtuse sellel \(x\)-i väärtusel).

Y — mida me ennustame (dependent variable, predicted variable).
X — mille põhjal me ennustame (independent variable, predictor).
Muutuja (variable) — iga asi, mida me valimis mõõdame (X ja Y on kaks muutujat). Muutujal on sama palju fikseeritud väärtusi kui meil on selle muutuja kohta mõõtmisandmeid.
Parameeter (parameter) — mudeli koefitsient, millele võib omistada suvalisi väärtusi. Parameetreid tuunides fitime mudeli võimalikult hästi sobituma andmetega.

Mudel on matemaatilise formalism, mis püüab kirjeldada füüsikalist protsessi. Statistilise mudeli struktuuris on komponent, mis kirjeldab ideaalseid ennustusi (nn protsessi mudel) ja eraldi veakomponent (ehk veamudel), mis kirjeldab looduse varieeruvust nende ideaalsete ennustuste ümber. Mudeli koostisosad on (i) muutuja, mille väärtusi ennustatakse, (ii), muutuja(d), mille väärtuste põhjal ennustatakse, (iii) parameetrid, mille väärtused fititakse ii põhjal ja (iv) konstandid.

4.4 Mudeli fittimine

Mudelid sisaldavad nii (1) matemaatilisi struktuure, mis määravad mudeli tüübi, kui (2) parameetreid, mida saab andmete põhjal tuunida, niiviisi täpsustades mudeli kuju ehk paiknemist matemaatlises ruumis. Näiteks võrrand \(y = a + bx\) määrab mudeli, kus \(y = x\) on see struktuur, mis tagab, et mudeli tüüp on sirge, ning \(a\) ja \(b\) on parameetrid, mis määravad sirge asendi. Seevastu struktuur \(y = x + x^2\) tagab, et mudeli \(y = a + b_1x + b_2x^2\) tüüp on parabool, ning parameetrite \(a\), \(b_1\) ja \(b_2\) väärtused määravad selle parabooli täpse kuju. Ja nii edasi.

Mudeli parameetrite tuunimist nimetatakse mudeli fittimiseks. Mudelit fittides on eesmärk saavutada antud tüüpi mudeli maksimaalne sobivus andmetega (kus “andmed” hõlmavad nii valimiandmeid kui taustateadmisi). Sellele tegevusele annab mõtte meie lootus, et mudeli tüüp kajastab mingit looduses toimuvat protsessi, mis meile teaduslikku huvi pakub. Ning, kuigi mudeli fit maksimeeritakse mudeli tüübi kohta, püüab see andmete vaatenurgast vaadatuna olla optimaalne, mitte maksimaalne (vt järgmine peatükk mudeli üle- ja alafittimisest). Kahjuks ei ole selline optimaalsus kuigi hästi matemaatilisse vormi valatav, ega ka mingi (pool)automaatse meetodiga empiiriliselt kontrollitav. Siin on tegu pigem teadlase sooviga, mille filosoofiline eeldus on, et meie andmetes on peidus nii andmeid genereeriva loodusliku protsessi üldine olemus (essents), kui juhuslik müra ehk valimiviga, ning et mudeli üldine kuju (sirge, parabool, jms) on juhtumisi sobiv just selleks, et neid kahte omavahel lahku ajada.

Lineraarse mudeli parima sobivuse andmetega saab tagada kahel erineval viisil: (i) vähimruutude meetod (Legendre, 1805; Gauss, 1809) mõõdab y telje suunaliselt iga andmepunkti kauguse mudeli ennustusest, võtab selle kauguse ruutu, summeerib kauguste ruudud ning leiab sirge asendi, mille korral see summa on minimaalne; (ii) Bayesi teoreem (Laplace, 1774) annab väheinformatiivse priori korral praktiliselt sama fiti. Olulise erinevusena võtab vähimruutude meetod arvesse ainult valimiandmed, samas kui Bayesi teoreemi kasutades fitime mudeli koefitsiente nii valimiandmete kui taustateadmiste peal (vt 8. ptk).

Hea mudel on

Võimalikult lihtsa struktuuriga, mille põhjal on veel võimalik teha järeldusi protsessi kohta, mis genereeris mudeli fittimiseks kasutatud andmeid;
Sobitub piisavalt hästi andmetega (eriti uute andmetega, mida ei kasutatud selle mudeli fittimiseks), et olla relevantne andmeid genereeriva protsessi kirjeldus;
Genereerib usutavaid simuleeritud andmeid.

Sageli fititkse samade andmetega mitu erinevat tüüpi mudelit ja püütakse otsustada, milline neist vastab kõige paremini eeltoodud tingimustele. Näiteks, kui sirge suudab kaalu järgi pikkust ennustada paremini kui parabool, siis on sirge mudel paremas kooskõlas teadusliku hüpoteesiga, mis annaks mehhanismi protsessile, mille käigus kilode lisandumine viiks laias kaaluvahemikus inimeste pikkuse kasvule ilma, et pikkuse kasvu tempo kaalu tõustes langeks. Samas, see et me oleme oma andmeid fittinud n mudeliga ja otsustanud, et mõned neist on paremad kui teised, ei tähenda, et mõni meie mudelitest oleks hea ka võrdluses tegeliku looduses valitseva olukorraga. Mudelid on pelgalt matemmatilised formalismid, mis võivad, aga kindlasti ei pea, kajastama füüsikalist maailma, ja meie mudelitevalik sõltub meile jõukohasest matemaatikast. Siinkohal ei tasu unustada, et matemaatika kirjeldab eelkõige abstraktseid mustreid, mitte otse füüsikalist maailma.

See, et teie andmed sobivad hästi mingi mudeliga, ei tähenda automaatselt, et see fakt oleks teaduslikult huvitav. Mudeli parameetrid on mõtekad mudeli matemaatilise kirjelduse kontekstis, aga mitte tingimata suure maailma põhjusliku seletamise kontekstis. Siiski, kui mudeli matemaatiline struktuur loodi andmeid genreeeriva loodusliku protsessi olemust silmas pidades, võib mudeli koefitsientide uurimisest selguda olulisi tõsiasju suure maailma kohta.

Mudeli fittimine: X ja Y saavad oma väärtused otse andmetest; parameetrid võivad omandada ükskõik millise väärtuse.

Fititud mudelist ennustamine: X-le saab omistada ükskõik millise väärtuse; parameetrite väärtused on fikseeritud; Y väärtus arvutatakse mudelist.

4.4.1 Üle- ja alafittimine

Osad mudelite tüübid on vähem paindlikud kui teised (parameetreid tuunides on neil vähem liikumisruumi). Kuigi sellised mudelid sobituvad halvemini andmetega, võivad need ikkagi paremini kui mõni paindlikum mudel välja tuua andmete peidetud olemuse. Statistiline mudeldamine eeldab, et me usume, et meie andmetes leidub nii müra (mida mudel võiks ignoreerida), kui signaal (mida mudel püüab tabada). Ilma signaalita süsteemi poleks arusaadavatel põhjustel mõtekas mudeldada ja ilma mürata süsteemi mudel tuleks ilma varieeruvuse (vea) komponendita, ehk deterministlik. Kuna mudeli jaoks näeb müra samamoodi välja kui signaal, on iga mudel kompromiss üle- ja alafittimise vahel. Me lihtsalt loodame, et meie mudel on piisavalt jäik, et mitte liiga palju müra modelleerida ja samas piisavalt paindlik, et piisaval määral signaali tabada.

Üks kõige jäigemaid mudeleid on sirge, mis tähendab, et sirge mudel on suure tõenäosusega alafittitud. Keera sirget kuipalju tahad, ikka ei sobitu ta enamiku andmekogudega. Ja need vähesed andmekogud, mis sirge mudeliga sobivad, on genereeritud teatud tüüpi lineaarsete protsesside poolt. Sirge on seega üks kõige paremini tõlgendatavaid mudeleid. Teises äärmuses on polünoomsed mudelid, mis on väga paindlikud, mida on väga raske tõlgendada ja mille puhul esineb suur mudeli ülefittimise oht. Ülefititud mudel järgib nii täpselt valimiandmeid, et sobitub hästi valimis leiduva juhusliku müraga ning seetõttu sobitub halvasti järgmise valimiga samast populatsioonist (igal valimil on oma juhuslik müra). Üldiselt, mida rohkem on mudelis tuunitavaid parameetreid, seda paindlikum on mudel, seda kergem on seda valimiandmetega sobitada ja seda raskem on seda tõlgendada. Veelgi enam, alati on võimalik konstrueerida mudel, mis sobitub täiuslikult kõikide andmepunktidega (selle mudeli parameetrite arv = N). Selline mudel on täpselt sama informatiivne kui andmed, mille põhjal see fititi — ja täiesti kasutu.

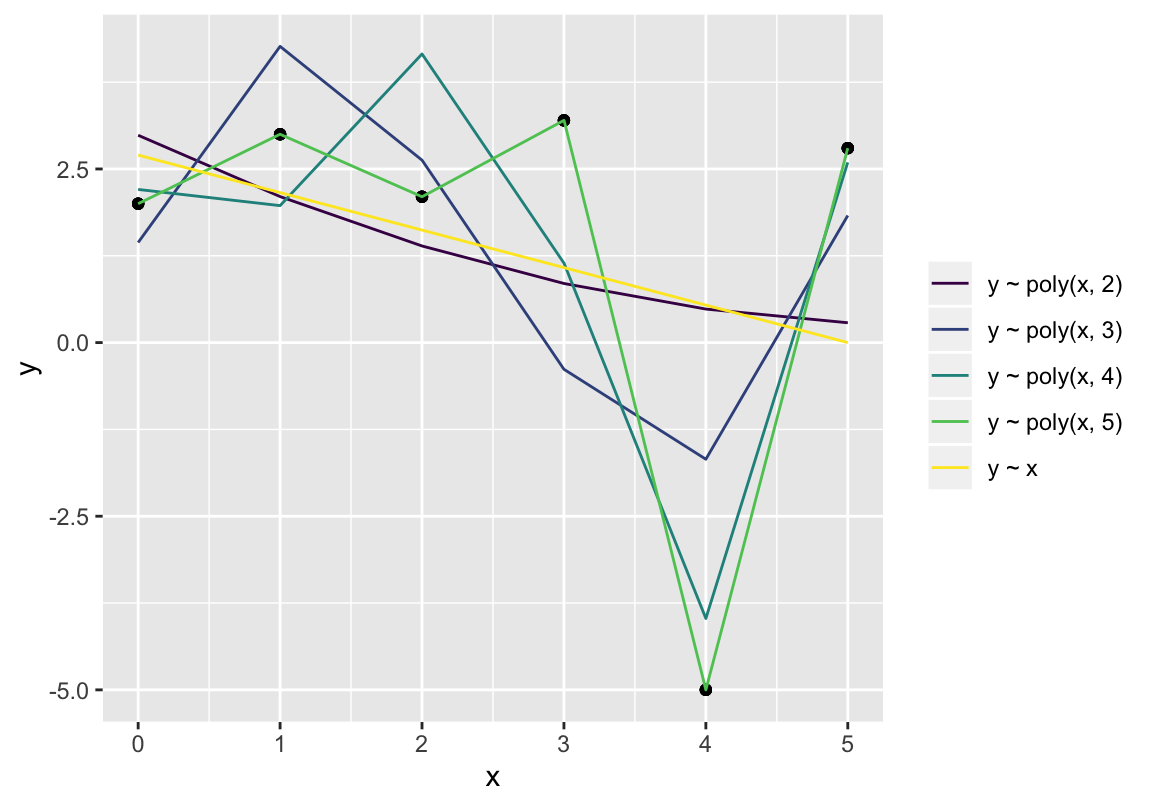
Joonis 4.7: Kasvava paindlikusega polünoomsed mudelid.

Vähimruutude meetodil fititud mudeleid saame võrrelda AIC-i näitaja järgi. AIC - Akaike Informatsiooni Kriteerium - vaatab mudeli sobivust andmetega ja mudeli parameetrite arvu. Väikseim AIC tähitab parimat fitti väikseima parameetrite arvu juures (kompromissi) ja väikseima AIC-ga mudel on eelistatuim mudel. Aga seda ainult võrreldud mudelite hulgas. AIC-i absoluutväärtus ei loe - see on suhteline näitaja.

model_formula	aic
y ~ x	35.0
y ~ poly(x, 2)	37.0
y ~ poly(x, 3)	36.1
y ~ poly(x, 4)	32.5
y ~ poly(x, 5)	-Inf

AIC näitab, et parim mudel on mod_e4. Aga kas see on ka kõige kasulikum mudel? Mis siis, kui 3-s andmepunkt on andmesisestaja näpuviga?

Ülefittimise vältimiseks kasutavad Bayesi mudelid informatiivseid prioreid, mis välistavad ekstreemsed parameetriväärtused. Vt http://elevanth.org/blog/2017/08/22/there-is-always-prior-information/

4.5 Lineaarse regressiooni eeldused

Matemaatilised eeldused:

Lineaarsus: ennustus Y-muutujale on lineaarne funktsioon prediktoritest \(Y = \beta_1X_1 + \beta_2X_2 +···\beta_nX_n\), ehk ekvivalentselt: kõikidel X-i väärtustel keksmine residuaal = 0.
homoskedastilisus ehk konstantne Y-muutuja suunaline varieeruvus kõigil X-i väärtustel. See tähendab ühtlasi residuaalide konstantset varieeruvust.
Normaalsus - residuaalid on normaaljaotusega, ehk Y-muutuja on normaaljaotusega kõigil X-i väärtustel.
Sõltumatus - residuaalide väärtused ei ole omavahel korreleeritud.
X-muutuja suunal puudub mõõtmisviga ja ebakindlus, mis tähendab, et x-i väärtused on täpselt teada (me ei ennusta neid). See eeldus on tähtis siis, kui püüame anda regresioonimudelile põhjusliku tõlgenduse. Mudelis \(Y = \alpha + \beta_1X_1 + \beta_2X_2\) viib mõõtmisviga \(X_2\)-s \(\beta_2\) koefitsiendi nulli suunas ja ühtlasi vähendab \(\beta_2X_2\) liikme mõju \(\beta_1\) fittimisel.
X-muutuja ei ole konstant vaid sisaldab erinevaid väärtusi.
Mitme prediktoriga lineaarse regressiooni puhul tuleb sisse veel kollineaarsuse eeldus: me eeldame, et ükski prediktorite paar pole täiuslikult lineaarselt korreleeritud (pole lineaarne funktsioon üksteisest).

Eeldused praktilise tähtsuse järjekorras:

Valiidsus – sa mõõdad asju, mis on relevantsed teadusliku küsimuse seisukohast. Näiteks, kui soovite mõõta kolesterooli alandava ravimi mõju, on mõistlik mõõta suremust, mitte pelgalt kolesterooli taset veres.
Esinduslikkus – andmed peaksid olema esinduslikud laiema populatsiooni suhtes. Väikesed ja kallutatud valimid ei ole sageli esinduslikud.
Lineaarsus ja sellest tulenev mudeli additiivsus. Väga tähtis on, et lineaarse regressiooniga mõõdetavad seosed oleks ka tõesti lineaarsed. Kui lineaarsusega on probleeme, võib aidata prediktorite transformeerimine (log(x) või 1/x) või uute prediktorite mudelisse lisamine. Samuti on võimalik prediktoritena samasse mudelisse panna nii \(x\) kui \(x^2\). Näiteks kui me paneme mudelisse nii muutuja \(vanus\) kui ka \(vanus^2\), saame modelleerida seost, kus y vanuse kasvades alguses kasvab ja siis kahaneb (aga ka U kujulist seost vanusega). Sellisel juhul võib olla ka mõistlik rekodeerida vanus kategooriliseks muutujaks (näit 4 vanuseklassi), mille tasemeid saab siis ükshaaval vaadata.
Sõltumatus. Selle eelduse rikkumine viib liiga kitsastele usalduspiiridele.
Vigade võrdne varieeruvus (homoskedastilisus) ja vigade normaalsus on vähemtähtsad. Log-normaalsete vigadega võiks lineaarsel regresioonil mudeldada log(Y) skaalas (vähimruutude meetodil) või Bayesi regressioonil mittelineaarset lognormaalset tõepäramudelit kasutades (vt. ptk 13).
Kollineaarsus. Täieliku kolineaarsuse korral mudel ei lahendu, aga sellisel juhul on põhjuseks enamasti viga mudeli spetsifitseerimisel. Osaline, aga ikkagi väga kõrge, kollineaarsus, mis õnneks on praktikas pigem haruldane, viib koefitsientide laiadele veapiiridele. Kui veapiirid pole laiad, siis pole ka kollineaarsust.

Regressioon kui kirjeldus ja kui põhjuslik hüpotees

Regressioonanalüüsi võib vaadelda 1) empiirilise kirjeldusena y ja x-i koos-varieerumisest või 2) muutujate vaheliste põhjuslike suhete analüüsina. Esimesel juhul ei tõlgenda me x ja y suhet x-i mõjuna y-le ja senikaua kui mudeli fit väljaspool andmeid, mida kasutati selle mudeli fittimiseks, on piisavalt hea, ei ole võimalik, et me fitime vale struktuuriga mudeli. Kui me fitime 2 mudelit (i) \(Y = \alpha + \beta_1X_1\) ja (ii) \(Y = \alpha + \beta_1X_1 + \beta_2X_2\), siis eeldame, et kahe mudeli \(\beta_1\) koefitsiendid tulevad erinevad. Aga sellest pole midagi, sest need kirjeldavad mõlemal juhul vaid empiirilisi seoseid.

Teisel, põhjuslikul juhul on kõik teisiti. Eeldades et \(X_2\) on üks Y-i põhjustest, on nüüd esimese mudeli veakomponendis peidus ka \(\beta_2X_2\). Kui \(X_1\) ja \(X_2\) on omavahel korreleeritud, siis tekib meil seetõttu ka korrelatsioon \(X_1\) ja veakomponendi vahel, mis rikub mudeli eeldusi, kallutades mudeli fittimisel meie hinnangut \(\beta_1\)-le, misläbi osa \(X_2\) mõjust Y-le omistatakse ekslikult \(X_1\)-le. See kõik juhtub siis, kui teise mudeli \(\beta_2\) ei ole null ja esineb \(X_1\) ja \(X_2\) vaheline põhjuslik seos.

Selle kallutatuse tõlgendamine sõltub omakorda \(X_1\) ja \(X_2\) vahelise põhjusliku seose struktuurist. Oluline on mõista, et regressioonimudeli enda struktuuris ei ole põhjuslikku infot - mudel ei tea isegi põhjuslikkuse olemasolust. Seega on meil lisaks regressioonimudelile vaja iseseisvat põhjuslike mõjude mudelit, mille formuleerime puhtalt teaduslikest asjaoludest lähtuvalt.

Kõige lihtsam selline mudel vastab randomiseeritud eksperimendile, kus me võrdleme katse- ja kontrolltingimust. Siin me usume, et kui katsetingimus (ravimi manustamine) mõjutab võrreldes kontrolltingimusega (platseeboga) katse väljundit (suremust), siis me oleme näidanud, et vastav ravim vähendab suremust. Seega on meie põhjuslik skeem ravim –> suremus ja regressioonimudel suremus~ravim, mis sisuliselt taandub kahe grupi keskmiste suremuste võrdlusele.

Kuidas on aga asjalood siis, kui meil ei lubata katset teha? Näiteks, kuidas määrata suitsetamise mõju kopsuvähile? Siin ei ole meil tegemist randomiseeritud katsega (me ei tohi jagada populatsiooni juhuslikult kahte gruppi ja sundida neist ühte suitsetama). Seega peame kasutama statistilisi meetodeid, et kontrollida oma tulemust nn confounderite vastu. Siin on lihtsaim regressioonimudel vähk ~ suitsetamine + muutuja_1 + …

Aga muutujaid on maailmas palju ja meil peab olema mingi reegel, mille järgi otsustada, millised neist additiivsesse mudelisse sisse panna ja millised välja jätta. Mudeli ennustusjõu maksimeerimine siin ei aita. Selle asemel peame mõistma võimalike põhjuslike skeemide suhet mitmese regressioonimudelitega. Põhjuslikud skeemid on nagu legod, mis kombineerivad endis nelja loogiliselt võimalikku ehitusplokki.

toru: x –> z –> y

#> Warning: Prefixing `UQ()` with the rlang namespace is deprecated as of rlang 0.3.0.
#> Please use the non-prefixed form or `!!` instead.
#> 
#>   # Bad:
#>   rlang::expr(mean(rlang::UQ(var) * 100))
#> 
#>   # Ok:
#>   rlang::expr(mean(UQ(var) * 100))
#> 
#>   # Good:
#>   rlang::expr(mean(!!var * 100))
#> 
#> This warning is displayed once per session.

Kui me tahame teada, kas x (põhjus) mõjutab y-t (tagajärge), siis toru puhul mudel \(tagajärg \sim põhjus + z\) vähendab x-i mõju (sest see mõju käib läbi z-i). Samas, mudel \(tagajärg \sim põhjus\) näitab x-i mõju. Seega, kumba mudelit kasutada sõltub sellest, kas me tahame näidata x-i otsest või kaudset mõju y-ile.

Järgnev skeem illustreerib olukorda, kus me tahame testida rohelist otseteed põhjuse ja tagajärje vahel ja selleks peame sulgema kõrvaltee, ehk tagaukse. Tagaukse sulgemiseks konditsioneerime oma regressioonimudeli z-l, ehk lisame z-i mudelisse \(tagajärg \sim põhjus + z\).

kahvel: x <– z –> y

Kahvli puhul regressioonimudel \(y \sim x\) näitab x-i mõju y-le (ehkki meie põhjuslikkuse mudelis puudub x ja y vaheline põhjuslik seos), aga mudel \(y \sim x + z\) välistab selle mõju. Seega peaksime sellise põhjusliku hüpoteesi korral mudelisse z-i sisse panema, sest see aitab kontrollida z konfounding mõju vastu.

Jällegi, kahvlist tagaukse sulgemiseks lisame z-i oma mudelisse \(tagajärg \sim põhjus + z\).

laupkokkupõrge: x –> z <– y

Laupkokkupõrke korral on olukord eelnevaga vastupidine. Nüüd avab mudel \(y ~ x + z\) tagaukse ja laseb z-i segava mõju mudelisse sisse, mis tekitab meile võlts-põhjusliku suhte x ja y vahel.

Laupkokkupõrke korral on tagauks suletud senikaua, kui me ei lisa z-i oma mudelisse.

järglane: see on toru, kus z-i juurest hargneb veel üks nool D-le. Siin saame me mudelisse A lisades ligikaudu sama tulemuse, mis z-i lisades. Seega, kui z-i väärtused pole meile teada, võime hädaga ka A-d kasutada.

Joonis 4.8: järglane

Joonis 4.9: järglane

Järglasest tagaukse võib sulgeda nii z-i (eelistatult) kui D (kui z on küll maailmas olemas, kuid puudub meie andmetest) mudelisse lisamise kaudu, aga ehk pole mõtet lisada mõlemat, sest z ja D võivad olla tugevalt kollineaarsed ehk omavahel korreleeritud.

Näiteks võib meil tekkid olukord, kus testime suitsetamise mõju vähile, aga ühtlsi usume, et inimeste elukoht mõjutab iseseisvalt nii vähki kui suitsetamist (tööstuslinnades haigestuvad ka mittesuitsetajad enam vähki, aga neis elav töölisklass ka suitsetab rohkem). Selles põhjuslikus skeemis töötab vanus kahvlina, millega arvestamiseks tuleb see regressioonimudelisse muutujana sisse panna: \(vähk \sim suits + vanus\).

Ja lõpuks tähtis tähelepanek, et meie põhjuslikes skeemides mängivad oma rolli ka need muutujad, mida me mõõtnud ei ole. Me usume, et isade (ja emade) haridustase on põhjuslikus seoses nende laste haridustasemega (isa –> laps). Oletame, et tahame uurida põhjuslikku hüpoteesi, mille kohaselt ka vanaisa haridustase mõjutab otseselt nende lapselaste haridustaset (vanaisa –> laps). Aga loomulikult usume me ka, et vanaisa haridustase mõjutab tema laste haridustaset (vanaisa –> isa). Seega saame loogilise skeemi torukujulise tagauksega, mille sulgemiseks peame fittima mudeli \(laps \sim vanaisa + isa\)

Aga mõtleme enne korra järele. Me ei oma küll andmeid oma andmestikus olevate inimeste elukohtade kohta, aga see on ikkagi tähtis. Nimelt elavad isad üldiselt koos oma lastega, aga lahus vanaisadest. Ja osad elukohad (näiteks ülikoolilinnad ja ooperiteatrite lähipiirkonnad) võivad mõjuda soodsalt hariduse omandamisele, samas kui teised piirkonnad võivad seda pärssida. Seega täiendame oma põhjuslikkusemudelit:

Siin on küsimärgiga tähistatud muutuja, mida ei ole (elukoht). Selles mudelis tekkib laupkokkupõrge vanaisa –> isa <– ?, ja kui me isa mudelisse paneme, et sulgeda toru vanaisa –> isa –> laps, siis avame sellega uue tagaukse. Siin ei paistagi tagauste sulgemiseks muud lahendust kui mudel \(laps \sim vanaisa + ?\), aga selle fittimiseks peame me küsimärgi asendama elukohaga, ehk kätte saama elukohaandmed ja need muutujana oma andmestikku panema. Seega lähevad ka meile kättesaamatud andmed põhjuslikku mudelisse sisse, ja ka neist sõltub, kas meil on üldse mõtet regressioonimudelit fittima hakata.