11 Järeldav statistika

Kui EDA määrab graafiliste meetoditega andmete kvaliteeti ja püstitab uusi hüpoteese, siis järeldav statistika püüab formaalsete arvutuste abil vastata kahele lihtsale küsimusele: 1. mis võiks olla kõige usutavam parameetriväärtus? ja 2. kui suur ebakindlus seda hinnangut ümbritseb? Kuna andmed tulevad meile lõpliku suurusega valimina koos mõõtmisveaga ja bioloogilise varieeruvusega, on ebakindlus hinnagusse sisse ehitatud. Hea protseduur kvantifitseerib selle ebakindluse ausalt ja täpselt – siin ei ole eesmärk niivõrd mitte ebakindlust vähendada (seda teeme eelkõige katse planeerimise tasemel), vaid seda kirjeldada. Järeldav statistika püüab, kasutades algoritme ja mudeleid, teha andmete põhjal järeldusi looduse kohta.

Ebakindluse allikad on mõõtmisviga, bioloogiline varieeruvus, mudeli viga (matemaatiline jaotusfunktsioon ei vasta looduses toimuvale), algoritmi viga (algoritm ei tee seda, mida kasutaja tahab) ja süstemaatiline viga (juhtub, kui te saate valesti aru oma katsesüsteemist, harrastate teaduslikku pettust või teete kõike muud, mis kallutab teie andmeid). Süstemaatilist viga ei saa kunagi välistada – see on loogiline paratamatus, mis tuleneb asjaolust, et andmeid on alati vähem kui on võimalikke süstemaatilise vea allikaid (ja sest lisaks ei ole meil kunagi täielikku nimekirja võimalikest vea allikatest), mille vahel saab loogiliselt vahet teha ainult neidsamaseid andmeid kasutades. Seega on vea allikad, millest igaüks on vaadeldav eraldiseisva alternatiivse teadusliku hüpoteesina meie põhihüpoteesile, andmete poolt loogiliselt alamääratud, mis tähendab et kindel teadmine teaduses on loogiliselt võimatu. Seega ulatuvad teaduslikud hüpoteesid alati teistpoole andmeid, ehk need ütlevad rohkem, kui oleks võimalik puhtalt andmete põhjal õigustada, ja sisaldavad usukomponenti. See on üks põhjus, miks me sõandame riskida mudelite kasutamisega oma hüpoteeside kinnitamisel.

Sellisel tegevusel on mõtet ainult siis, kui ühest küljest andmed peegeldavad tegelikkust ja teisest küljest tegelikkus hõlmab enamat, kui lihtsalt meie andmeid. Kui andmed = tegelikkus, siis pole mõtet keerulisi mudeleid kasutada – piisab lihtsast andmete kirjeldusest. Ja kui andmetel pole midagi ühist tegelikkusega, siis on need lihtsalt ebarelevatsed. Seega on järeldava statistika abil tehtud järeldused alati rohkem või vähem ebamäärased ning meil on vaja meetodit selle ebamäärasuse mõõtmiseks. Selle meetodi annab tõenäosusteooria.

Järeldav statistika on tõenäosusteooria käepikendus

See õpik õpetab Bayesi statistikat, mis põhineb tõenäosusteoorial. Tänu sellele moodustab Bayesi statistika sidusa terviku, mille abil saab teha kõike seda, mida saab teha tõenäosusteooria abil. Bayesi statistika põhineb Bayesi teoreemil, mis on triviaalne tuletus tõenäosusteooria aksioomidest. Tänu Cox-i teoreemile (1961) teame, et klassikaline lausearvutuslik loogika on tõenäosusteooria erijuht ning, et Bayesi teoreem on teoreetiliselt parim viis tõenäosustega töötamiseks. Seega, kui te olete kindel oma väidete tõesuses või vääruses, siis on klassikaline loogika parim viis nendega opereerida; aga kui te ei saa oma järeldustes päris kindel olla, siis on teoreetiliselt parim lahendus tõenäosusteooria ja Bayesi teoreem.

Lisaks kooskõlalisusele tõenäosusteooriaga eristab Bayesi statistikat 
klassikalisest sageduslikust statistikast kaks põhilist asjaolu: Bayesis 
kasutatakse episteemilist tõenäosuse tõlgendust, mille kohaselt tõenäosus 
mõõdab usu määra hüpoteesi kehtimisse, ja teiseks, iga Bayesi arvutus 
sisaldab lisaks andmetele meie neist andmetest sõltumatut hinnangut hüpoteesi
kehtimise tõenäosusele (see hinnang on formaliseeritud nn eeljaotuses ehk
eeltõenäosuses ehk prioris). Ortodoksne nn sageduslik statistika kasutab 
seevastu nn objektiivset ehk sageduslikku tõenäosuse tõlgendust ja ei kasuta
eeltõenäosusi oma arvutustes. Põhjalikumat seletust vt allpool ja lisa 1.

Tõenäosusteooria on aksiomaatiline süsteem, mille abil saame omistada numbriline väärtuse meie usu määrale mingisse hüpoteesi. Näiteks, kui me planeerime katset, kus me viskame kulli ja kirja ja teeme seda kaks korda, siis saame arvutada, millise tõenäosusega võime oodata katse tulemuseks kaht kirja. Aga seda tingimusel, et me võtame omaks mõned eeldused – näiteks et münt on aus ja et need kaks viset on üksteisest sõltumatud.

Sellel katsel on 4 võimalikku tulemust: H-H, H-T, T-H, T-T (H - kull, T - kiri). Tõenäosus saada 2-l mündiviskel 2 kirja, P(2 kirja) = 1/4, P(0 kirja) = 1/4 ja P(1 kiri) = 2/4 = 1/2. Sellega oleme andnud oma katseplaanile täieliku tõenäosusliku kirjelduse (pane tähele, et 1/4 + 1/4 + 1/2 = 1). Ükskõik kui keeruline on teie katseplaan, põhimõtteliselt käib selle tõenäosusteoreetiline analüüs samamoodi. Tõenäosusteooria loomus seisneb kõikide võimalike sündmuste üleslugemises ja erinevat tüüpi sündmuste suhteliste sageduste arvutamises – ning senikaua, kui me seda nüri järjekindlusega teeme, on vastus, mille me saame, tõsikindel.

Ehkki Bayesi statistika põhineb tõenäosusteoorial ja on sellega kooskõlas, ei ole see sama asi, mis tõenäosusteooria. Statistikas pööratakse tõenäosusteoreetiline ülesanne pea peale ja küsitakse nii: kui me saime 2-l mündiviskel 2 kirja, siis millise tõenäosusega on münt aus (tasakaalus)? Erinevus tõenäosusteoreetilise ja statistilise lähenemise vahel seisneb selles, et kui tõenäosusteoorias me eeldame, et teame, kuidas süsteem on üles ehitatud, ja ennustame sellest lähtuvalt võimalike (hüpoteetiliste) andmete tõenäosusi, siis statistikas me kontrollime neid eeldusi päriselt olemasolevate andmete põhjal. Seega annab tõenäosusteooria matemaatiliselt tõsikindlaid vastuseid ideaalmaailmade kohta, samas kui statistika püüab andmete põhjal teha järeldusi päris maailma kohta. Selleks kasutame Bayesi teoreemi (vt allpool).

Tõenäosusteooria määrab kõikide võimalike sündmuste esinemise tõenäosused, eeldades, et hüpotees H kehtib (H on siin lihtsalt teine nimi “eeldusele”).

Statistika hindab H-i kehtimise tõenäosuse lähtuvalt kogutud andmetest, matemaatilistest mudelitest ning taustateadmistest.

Tõenäosusteooria aksioomid on tuletatavad järgmistest eeldustest:

hüpoteesi usutavuse määra saab kirjeldada reaalarvudega 0 ja 1 vahel
ratsionaalne mõtlemine vastab kvalitatiivselt tervele mõistusele: tõendusmaterjal hüpoteesi toetuseks tõstab selle hüpoteesi usutavust.
mõtlemine peab olema konsistentne: kui me saame järeldusi teha rohkem kui ühel viisil, peame lõpuks ikkagi alati samale lõppjäreldusele jõudma
kogu kättesaadav relevantne informatsioon tuleb järelduste tegemisel arvesse võtta (totaalse informatsiooni printsiip)
ekvivalentsed teadmised on representeeritud ekvivalentsete numbritega.

Tõenäosusteooria aksioomid, mida on neli tükki, ütlevad tõlkes inimkeelde,

et iga sündmuse tõenäosus on suurem või võrdne nulliga - \(P(A) \geq 0\),
et loogiliselt paratamatu sündmuse tõenäosus on üks - \(P(\Omega)=1\). \(\Omega\) on sample space, mis koosneb üksteist välistavatest ja ammendavatest hüpoteesidest. Nende hüpoteeside tõenäosuste summa on 1, mis tähendab, et täpselt üks neist kehtib paratamatult.
et üksteist välistavate sündmuse puhul võrdub tõenäosus, et toimub üks või teine sündmus, nende sündmuste tõenäosuste summaga, ehk \(P(A \lor B) = P(A) + P(B)\).
et sündmuse A tõenäosus, juhul kui me eeldame sündmuse B kehtimist, võrdub nende kahe sündmuse koosesinemise tõenäosuse jagatisega sündmuse B tõenäosusest, ehk \(P(A~\vert~B) = \frac{P(A \land B)}{P(B)}\).

Sümbolite tähendused:

\(A \land B\) tähendab “A ja B”,
\(A \lor B\) tähendab “A või B”,
\(\lnot A\) tähendab mitte-A, ehk A == FALSE.
\(P(A~ \vert ~B)\) on tinglik tõenäosus, mida tuleks lugeda: “A tõenäosus tingimusel, et kehtib B”. Sellega me ei väida, et B päriselt kehtib, vaid küsime: “Kui peaks juhtuma, et B kehtib, milline oleks sellisel juhul A tõenäosus?”. Pane tähele, et \(P(vihm~\vert~pilves~ilm)\) ei ole numbriliselt sama, mis \(P(pilves~ilm~\vert~vihm)\).

Need aksioomid, mis oma matemaatilises vormis postuleeriti Andrei Kolmogorovi poolt ca 1933, peaksid olema iseenesestmõistetavad ja ainult neist on tuletatud kogu tõenäosusteooria. Tõenäosusteooria on matemaatika haru, mis tähendab, et sümbolitel P, A, B, jms ei ole selles muud fikseeritud tähendust, kui et need käituvad vastavalt tõenäosusteooria aksioomidele ja neist dedutseeritud teoreemidele. Nendes piirides võime anda neile sümbolitele anda ükskõik millise tähenduse, mis siis seob matemaatilise struktuuri päris maailmaga, mis ei ole oma loomuselt matemaatiline formalism. Näiteks \(P(A~\vert~B)\) võib tähendada “hüpoteesi A tõenäosust tingimusel, et meil on andmed B”, aga sama hästi ka “andmete A tõenäosust tingimusel, et kehtib hüpotees B”, või ka midagi muud. \(P(A)\) võib meie jaoks tähistada “hüpoteesi tõenäosust”, “andmete tõenäosust”, “tõendusmaterjali tõenäosust” ja “sündmuse tõenäosust”, aga ka “homse vihma tõenäosust” või “tõenäosust, et parameetri väärtus > 2”).

\(A \lor \lnot A\) tähistab loogiliselt paratamatut ehk loogiliselt tõest propositsiooni ja \(A \land \lnot A\) tähistab loogiliselt vastuolulist ehk loogiliselt väärat propositsiooni (propositsioon on defineeritud lausena, millele saab omistada tõeväärtuse). Loogiliselt väära propositsiooni tõenäosus on null ja loogiliselt tõese propositsiooni tõenäosus on üks (\(P(\lnot A) = 1 - P(A)\)).

Kui tõenäosused on 0 või 1, siis taandub tõenäosusteooria matemaatliselt oma erijuhule, milleks on lausearvutuslik loogika. Lausearvutusel on huvitav omadus, monotoonilisus, mille kohaselt kui juba on saavutatud loogiliselt valiidne tulemus, siis uute andmete lisandumisel ei saa me seda muuta. Seevastu tõenäosusteoorias ja statistikas muudavad uued andmed hüpoteesi kehtimise tõenäosust. Selles mõttes ei saa tõenäosuslik teadus kunagi valmis ja kui inimene on 100% veendunud mingi hüpoteesi/sündmuse tõesuses või vääruses, siis seisavad tema uskumused väljaspool teadust selles mõttes, et neid ei ole võimalik teaduslike argumentidega mõjutada.

Formaalsed tuletised tõenäosusteooria aksioomidest

Me anname siin 9 tuletust ilma tõestuskäikudeta, mis on aga lihtsad. Siin võib A ja B vaadelda erinevate sündmustena või hüpoteesidena. Me eeldame, et kummagi hüpoteesi tõenäosus > 0.

Tõenäosusteooria põhituletised:

\(0 \leq P(A) \leq 1\) - tõenäosused jäävad 0 ja 1 vahele
\(P(\lnot A) = 1 - P(A)\), üksteist välistavate ammendavate hüpoteeside tõenäosused summeeruvad ühiktõenäosusele.
\(P(A \And B) \le P(A)\); \(P(B) \leq P(A \lor B)\)
Kui B tuleneb deduktiivselt A-st ja \(P(A) > 0\), siis \(P(B~ \vert ~A) = 1\) ja \(P(\lnot B~ \vert A) = 0\). Siit tuleleb, et kui tõendusmaterjal e tuleneb deduktiivselt hüpoteesist H (H ennustab e-d) ja kui \(P(H) > 0\) ning \(P(e) < 1\), siis \(P(H~ \lvert~ e) > P(H)\), ehk e tõstab H tõenäosust.
Kui B tuleneb deduktiivselt A-st \([A \lor (B \land \lnot A) \Leftrightarrow B]\), siis \(P(B) \leq P(A)\).
Loogiliselt ekvivalentsed propositsioonid/hüpoteesid on sama tõenäosusega – kui \(A \Leftrightarrow B\), siis \(P(A) = P(B)\)
Üksteist välistavate propositsioonide korral \(P(A_1 \lor A_2 \lor ... \lor A_n) = P(A_1) + P(A_2) + ... + P(A_n)\) – see on finiitse additiivsuse printsiip.
Definitsioon: A ja B on üksteisest sõltumatud siis ja ainult siis kui \(P(A~ \vert B) = P(A)\)
Kui A ja B on üksteisest sõltumatud, siis \[P(A\land B) = P(A)P(B)\]
Kui A ja B ei ole üksteisest sõltumatud, siis \[P(A \lor B) = P(A) + P(B) - P(A \land B)\] ja kolmele sündmusele: \[\begin{array}{lcl} P(A \lor B \lor C) = P(A) + P(B) + P(C) - \\P(A \land B) - P(B \land C) - P(A \land C) + \\P(A \land B \land C) \end{array}\]
Totaalne ehk marginaalne tõenäosus: \[P(A) = P(A~\vert~B)P(B) + P(A~\vert~\lnot B)P(\lnot B)\] ehk \[P(A) = P(A~\vert~B_1)P(B_1) + P(A~\vert~ B_2)P(B_2) + ...\] üksteist välistavatele B-dele.
Bayesi teoreem: \[P(A~\vert~B) =\frac{P(A)P(B~\vert~A)}{P(B)}\] kus vastavalt 15. punktile \[P(B) = P(A)P(B~\vert~A) + P(\lnot A)P(B~\vert~\lnot A)\] või \[P(B) = P(A_1)P(B~\vert~A_1) + P(A_2)P(B~\vert~A_2) + ...\]

Bayesi teoreemi kasutatakse määramaks hüpoteesi tõenäosuse pärast uute faktide (andmete) lisandumist olemasolevatele teadmistele. Selleks peab hüpoteesiruum olema jagatud vähemalt kaheks ammendavaks ja üksteist välistavaks hüpoteesiks. Kui A on H₁ ning mitte-A on ammendav ja välistav H₂ ja B tähistab andmeid (data), saame Bayesi teoreemi ümber kirjutada

\[P(H_1~\vert~data) = \frac{P(H_1)P(data~\vert~H_1)}{ P(H_1)P(data~\vert~H_1) + P(H_2)P(data~ \vert ~H_2)}\]

\(P(H_1~\vert~data)\) on \(H_1\) kehtimise tõenäosus meie andmete korral – ehk posteerior,

\(P(H_1)\) on \(H_1\) kehtimise eelnev, ehk meie andmetest sõltumatu, tõenäosus – ehk prior,

\(P(data~\vert~H_1)\) on andmete esinemise tõenäosus tingimusel, et H₁ kehtib – ehk tõepära.

Jagamistehe tehakse ainult selle pärast, et normaliseerida 1-le kõikide hüpoteeside tõenäosuste summa meie andmete korral ja seega viia posteerior vastavusse tõenäosusteooria aksioomidega — kui meil on i ammendavat üksteist välistavat hüpoteesi, siis murrujoone alla läheb \(\sum~P(data~\vert~H_i)P(H_i) = 1\).

Bayesi teoreem on triviaalne tuletus tõenäosusteooria aksioomidest, milles pole midagi maagilist. See ei ole automaatne meetod, mis tagaks inimkonna teadmiste kasvu, vaid lihtsalt parim võimalik viis andmemudeli ja taustateadmiste mudeli ühendamiseks ja normaliseerimiseks tinglikuks tõenäosuseks (hüpoteesi tõenäosus meie andmete ja taustateadmiste korral). Edasi sõltub kõik mudelite, andmete ja taustateadmiste kvaliteedist.

Näited tõenäosusteooria tuletiste rakendamisest

Järgnevatel näidetel on ühist kaks asja: need on matemaatiliselt triviaalselt lihtsad, aga intuitiivselt lootusetult keerulised. Kõigi nende puhul on inimestel tugev intuitsioon, mis on vale – ja tõenäosusteooria tundmine ei anna meile paremat intuitsiooni. Seega, ainus, mis üle jääb, on iga probleemi taandamine tõenäosusteooria valemitele ja selle tuimalt läbi arvutamine.

7. Punkt Linda on 31 aastane, vallaline, sõnakas ja väga nutikas. Ta õppis ülikoolis filosoofiat ja muretses sel ajal sügavalt diskrimineerimise ja sotsiaalse õigluse pärast ning osales tuumarelva vastastel meeleavaldustel. Kumb on tõenäolisem? Linda on pangateller. Või Linda on pangateller, kes osaleb feministlikus liikumises. Kuigi enamus vastajatest eelistab 2. varianti, on see sõna otses mõttes loogikavastane.

13. Punkt Kui me viskame täringut 3 korda, kui suure tõenäosusega saame vähemalt ühe kuue? Naiivselt võiks arvata, et see tõenäosus on 50%. Kuid rakendades tõenäosusteooriat saame teistsuguse vastuse. Lihtsuse huvides defineerime küsimuse ümber: kui suure tõenäosusega ei saa me 3-l viskel ühtegi kuute? Vastus: kui igal viskel on 0 kuue tõenäosus 5/6, siis \((5/6)(5/6)(5/6) = 0.58\) ja \(1 - 0.58 = 0.42\), mis tähendab, et vähemalt 1 kuue (või ükskõik mis numbri ühest kuueni) saame 42% tõenäosusega. Teine näide (NYT 03-12-2017): te ostate maja Texases Hustonis, millele müüja annab garantii, et üleujutuse tõenäosus on 1% aastas. Seadus nimetab seda näidikut “100 aasta suurvee-tasemeks”. 1% näidu puhul ei pea te seaduse järgi ostma üleujutusekindlustust. Kui suure tõenäosusega tabab teie maja üleujutus pangalaenu perioodi vältel (30 aastat)? Vastus: \(1 - (99/100)^{30} = 0.26\).

14. Punkt Kui tõenäosus, et homme sajab pussnuge on 0.1 ja et ülehomme sajab pussnuge on 0.1, siis millise tõenäosusega sajab vähemalt ühel neist päevadest? Eeldades sündmuste sõltumatust: \[\begin{array}{lcl} P(homme~ sajab \lor ülehomme~ sajab) = \\0.1 + 0.1 - 0.1 \times 0.1 = 0.19\end{array}\] Kui me aga teame, et sadu erinevatel päevadel on korreleeritud näiteks nii: \[P(ülehomme~ sajab~ \vert~homme~sajab)= 0.2\] \[P(ülehomme~ sajab~ \vert~ \lnot homme~sajab)= 0.15\] siis \[\begin{array}{lcl} P(homme~ sajab \lor ülehomme~ sajab) = \\P(homme~ sajab) + P(ülehomme~ sajab) - \\P(homme~ sajab~ \And~ ülehomme~ sajab) \end{array}\] Nüüd peame arvutama \(P(ülehomme~sajab)\), kasutades 15. punkti (marginaliseerimist), misjärel saame valemi \[P(A \lor B)= P(A)+P(B)-P(A)P(B ~\vert~A)\] Kui vihm on korreleeritud, siis väheneb tõenäosus, et sajab vähemalt ühel päeval.

4. Punkt Meil on kolm pannkooki, millest esimesel on mõlemad küljed moosised, teisel on üks külg moosine ja kolmandal pole üldse moosi. Juhtus nii, et meile pandi taldrikule pannkook, mille pealmine külg on moosine. Millise tõenäosusega on moosine ka selle pannkoogi alumine külg? NB! Vastus ei ole 50%. Lahendus: Kui A - moos all, B - moos üleval, siis vastavalt 4. aksioomile \[P(moos~ all~ \lvert ~moos~üleval ) = \frac{P(moos~all \land ~moos~üleval)}{P(moos~all)}\] Tõenäosus, et moos on all ja üleval on 1/3 (me teame, et 1 pannkook 3st on mõlemalt küljelt moosine) ja tõenäosus, et moos on all, on keskmine kolmest tõenäosusest, millega me kolmel pannkoogil moosise külje saame: mean(c(1, 0.5, 0)) = 1/2. Seega, vastus on \((1/3)/(1/2) = 2/3\). Kui me saame moosise ülemise külje, siis on tõenäosus 2/3, et ka all on moos!

15. Punkt Kui A tähistab sündmust “ma sooritan eksami edukalt” ja B tähistab sündmust “ma õpin eksamiks”, ning meil on dihhotoomne valik: õpin / ei õpi, siis \[\begin{array}{lcl} P(hea~hinne) = P(õpin)P(hea~hinne~ \lvert ~õpin) + \\P(ei~ õpi)P(hea~hinne~ \lvert ~ei~õpi) \end{array}\] Ehk sõnadega kirjutatult: Hea hinde tõenäosus võrdub korrutisega kahest tõenäosusest – tõenäosus, et ma eksamiks õpin, ja tõenäosus, et ma saan hea hinde siis kui ma õpin –, millele tuleb liita teine korrutis kahest tõenäosustest – tõenäosus, et ma ei õpi, ja tõenäosus, et ma saan hea hinde ka ilma õppimata. Siit saad ise enda jaoks välja arvutada ennustuse, millise tõenäosusega just sina selle kursuse edukalt läbid.

16. Punkt Bayesi teoreemi rakendamine diskreetsetele hüpoteesidele: Oletame, et 45 aastane naine saab rinnavähi sõeluuringus mammograafias positiivse tulemuse. Millise tõenäosusega on tal rinnavähk? Kõigepealt jagame hüpoteesiruumi kahe diskreetse hüpoteesi vahel: H₁ - vähk ja H₂ - mitte vähk. Edasi omistame numbrilised väärtused järgmistele parameetritele:

H₁ tõepära, ehk tõenäosus saada positiivne mammogramm juhul, kui patsiendil on rinnavähk (testi sensitiivsus): \(P( +~\vert~H_1) = 0.9\)
H₂ tõepära, ehk tõenäosus saada positiivne mammogramm juhul, kui patsiendil ei ole rinnavähki (1 - testi spetsiifilisus): \(P( +~\vert~H_2) = 0.08\). Pane tähele, et 0.9 + 0.08 ei võrdu ühega, mis tähendab, et tõepära pole tõenäosusteooria mõttes päris tõenäosus.
Eelnev tõenäosus, et patsiendil on rinnavähk \(P(H_1) = 0.01\) (see on rinnavähi sagedus 45 a naiste populatsioonis; kui me teame patsiendi genoomi järjestust või rinnavähijuhte tema lähisugulastel, võib P(H₁) tulla väga erinev).
\(P(H_2) = 1 - P(H_1) = 0.99\)

Nüüd arvutame posterioorse tõenäosuse \(P(H_1~\vert~+)\)

likelihood_H1 <- 0.9
likelihood_H2 <- 0.08
prior_H1 <- 0.01
prior_H2 <- 1 - prior_H1
posterior1 <- likelihood_H1*prior_H1/
  (likelihood_H1*prior_H1 + 
     likelihood_H2*prior_H2)
posterior1
#> [1] 0.102

Nagu näha, postiivne tulemus rinnavähi sõeluuringus annab 10% tõenäosuse, et teil on vähk (ja 90% tõenäosuse, et olete terve). Selle mudeli parameetriväärtused vastavad enam-vähem tegelikele mammograafia veasagedustele ja tegelikule populatsiooni vähisagedusele.

Mis juhtub, kui me teeme positiivsele patsiendile kordustesti? Nüüd on esimese testi posteerior meile prioriks, sest see kajastab definitsiooni järgi kogu teadmist, mis meil selle patsiendi vähiseisundist on (muidugi eeldusel, et me esimese mudeli kohusetundlikult koostasime).

likelihood_H1 <- 0.9
likelihood_H2 <- 0.08
prior_H1 <- posterior1
prior_H2 <- 1 - prior_H1
posterior2 <- likelihood_H1*prior_H1/
  (likelihood_H1*prior_H1 + 
     likelihood_H2*prior_H2)
posterior2
#> [1] 0.561

Patsiendile võib pärast kordustesti positiivset tulemust öelda, et ta on 44% tõenäosusega vähivaba. Eelduseks on, et me ei tea midagi selle patsiendi geneetikast ega keskkonnast põhjustatud vastuvõtlikusest vähile ning, et testi ja kordustesti vead on üksteisest sõltumatud (mitte korreleeritud).

Bayesi teoreemi kasutamine pideva suuruse (näiteks keskväärtuse või standardhälbe) hindamiseks on põhimõtteliselt samasugune, ainult et nüüd on meil lõpmata suur arv hüpoteese (iga teoreetiliselt võimalik parameetri väärtus on siin “hüpotees”), mis tähendab, et vastavalt Bayesi teoreemile on meil vaja ka lõpmata hulka tõepärasid ja lõpmata hulka prioreid. Lõpmata hulk tõepärasid ja prioreid tähendab lihtsalt, et me avaldame need kahe pideva funktsioonina, misjärel saame neist kahest funktsioonist arvutada kolmanda pideva funktsiooni, posteeriori. Posteeriorist saab omakorda arvutada iga mõeldava parameetriväärtuste vahemiku tõenäosuse või usalduspiirid, milles mingi meie poolt etteantud tõenäosusega paikneb parameetri tegelik väärtus (vt ptk 10). Ja posterioorse funktsiooni tipp (mood) vastab kõige tõenäolisemale parameetriväärtusele.

Mida kitsam on posteerior, seda kitsamad tulevad sellest arvutatud usalduspiirid. Seega peaksime püüdma panna oma mudelitesse parameetreid (statistikuid), mille posteeriorid tulevad võimalikult kitsad (vt allpool ptk “ajalooline vahepala” selle kohta, kuidas aritmeetiline keskmine on selline statistik).

Tõenäosuse episteemiline tõlgendus

Tõenäosus P() ei ole matemaatiliselt midagi enamat, kui reaalarv, mis rahuldab Kolmogorovi aksioomide poolt seatud tingimusi. Seevastu tõenäosuse mõiste tõlgendus, mis rahuldaks teaduse vajadusi, on pigem filosoofiline kui matemaatiline probleem. Teisisõnu, tõenäosusteooria õpetab meid tõenäosustega matemaatiliselt ümber käima, kuid ei anna meile seost matemaatiliste tõenäosuste ja päris maailma vahel, ega ei ütle, mida tõenäosus teaduses tähendab. Kaasajal kasutatkse kahte põhilist tõenäosuse tõlgendust, episteemilist (e Bayesiaanlikku) ja objektiivset (e sageduslikku), millest me siin käsitleme esimest. Sagedusliku tõlgenduse kohta vt lisa 1.

Kuna kõik tõenäosuse tõlgendused alluvad samadele tõenäosusteooria 
aksioomidele, siis on kõik valiidsed tõenäosust sisaldavad argumendid 
tõlgitavad erinevate tõenäosuste tõlgenduste vahel. Seda on tähtis teada. 
Võtame näiteks olukorra, kus hüpotees h deduktiivselt ennustab 
tõendusmaterjali e-d ja lisaks oleks e väga ebatõenäoline juhul, kui h ei 
kehti. Paraku, isegi kui katse tulemus on tõepoolest e, ei saa me ikkagi 
ilma h-i eeltõenäosust P(h) kasutamata, öelda midagi h-i kehtimise tõenäosuse 
kohta meie andmete korral, sest Bayesi teoreem kehtib ühtmoodi kõikide 
tõenäosuse tõlgenduste korral. Aga just seda teevad pahatihiti teadlased 
(ja harvem statistikud), kes kasutavad traditsioonilist sageduslikku 
statistikat, mis ei sisalda formaaslseid meetodeid eeltõenäosuste arvesse 
võtmiseks. Teisalt pole matemaatilises mõttes vahet, millist tõenäosuse 
tõlgendust te parasjagu kasutate -- see on teie teaduslik ja filosoofiline 
eelistus, ja te võite tõenäosust vastavalt vajadusele kasvõi iga päev 
erinevalt tõlgendada.

Bayesiaanlik statistika opereerib episteemilise tõenäosusega. See tähendab, et tõenäosus annab numbrilise mõõdu meie ebakindluse määrale mõne hüpoteesi ehk parameetriväärtuse kehtimise kohta. Seega mõõdab tõenäosus meie teadmiste kindlust (või ebakindlust). Näiteks, kui arvutus näitab, et homme on vihma tõenäosus 60%, siis me oleme 60% kindlad, et homme tuleb vihma. Aga hoolimata sellest, mida me vihma kohta usume, homme kas sajab vihma või mitte, ja seega on homse vihma objektiivne tõenäosus meie akna taga 0 või 1 – ja mitte kunagi 0.6.

Tõenäosuse formaalne tõlgendus tuleb otse kihlveokontorist. Kui sa arvutasid, et vihma tõenäosus homme on 60%, siis see tähendab, et sa oled ratsionaalse olendina nõus maksma mitte rohkem kui 60 senti kihlveo eest, mis võidu korral toob sulle sisse 1 EUR – ehk 40 senti kasumit. Seega on “ausa kihlveo shansid” (fair betting odds) sinu jaoks 60:40 ehk 3:2 vihma kasuks, mis tähendab, et sa usud, et nende kihlveoshansidega oled sa enda jaoks tasakaalustanud riski nii võidu kui kaotuse korral ja usud, et pikas perspektiiviis jääd sa nii mängides nulli. Seega, ausa kihlveo shansid a:b annavad episteemilise tõenäosuse valemiga a/(a + b), ja tõenäosusest a saab sansid valemiga b = 1 - a.

Selles mõttes on Bayesi tõenäosus subjektiivne. Kui me teaksime täpselt, mis homme juhtub, siis ei oleks meil selliseid tõenäosusi vaja. Seega, kui te hoolimata kõigest, mida ma selle kohta eelpool kirjutanud olen, ikkagi usute, et teadus suudab tõestada väiteid maailma kohta samamoodi, nagu seda teeb matemaatika formaalsete struktuuride kohta, siis pääsete sellega statistika õppimisest ja kasutamisest. Aga kui te siiski arvutate Bayesi tõenäosusi, siis ei ütle need midagi selle kohta, kas maailm on tõenäosuslik või deterministlik. Inimesed, kes vajavad tõenäosusi maailma seisundite kirjeldamiseks, ei kasuta episteemilisi tõenäosusi, vaid sageduslikku tõlgendust.

Kui mõõdame pidevat suurust, näiteks inimeste pikkusi, siis saame arvutuse tagajärjel tõenäosused kõigi võimalike parameetriväärtuste kohta, ehk igale mõeldavale pikkuse väärtusele. Kuna pideval suurusel on lõpmata hulk võimalikke väärtusi, avaldame me sellised tõenäosused pideva tõenäosusfunktsioonina, e järeljaotusena e posteeriorina. Posteerior näeb sageli välja nagu normaaljaotus ja me võime selle põhjal arvutada, kui suur osa summaarsest tõenäosusest, mis on 1, jääb meid huvitavasse pikkuste vahemikku. Kui näiteks 67% posteeriori pindalast jääb pikkuste vahemikku 178 kuni 180 cm, siis me usume, et 0.67-se (67%-se) tõenäosusega asub tegelik keskmine pikkus kuskil selles vahemikus.

Tõenäosusteooriast tulenevad statistika põhiprintsiibid

statistilise analüüsi kvaliteet sõltub mudeli eeldustest & struktuurist. Kuna maailm ei koosne matemaatikast, teevad matemaatilised mudelid alati eeldusi maailma kohta, mis ei ole päris tõesed ja mida ei saa tingimata empiiriliselt kontrollida. Mündiviske näites eeldasime, et mündivisked olid üksteisest sõltumatud. Kui me sellest eeldusest loobume, läheb meie mudel keerulisemaks, sest me peame mudelisse lisama teavet visetevahelise korrelatsiooni kohta. Aga see keerulisem mudel toob sisse uued eeldused. Üldiselt peaks mudeli struktuur kajastama katse struktuuri, mis kaasaegses statistikas tähendab sageli hierarhilisi mudeleid.
statistilise analüüsi täpsus sõltub andmete hulgast. Kui kahe mündiviske asemel teeksime kakskümmend, siis saaksime samade eelduste põhjal teha oluliselt väiksema ebakindluse määraga järeldusi mündi aususe kohta.
statistilise analüüsi kvaliteet sõltub andmete kvaliteedist. Kui münt on aus, aga me viskame seda ebaausalt, siis, mida rohkem arv kordi me seda teeme, seda tugevamalt usub teadusüldsus selle tagajärjel millessegi, mis pole tõsi.
statistilise analüüsi kvaliteet sõltub taustateadmiste kvaliteedist. Napid taustateadmised ei võimalda parandada andmete põhjal tehtud järeldusi juhul, kui andmed mingil põhjusel ei vasta tegelikkusele. Adekvaatsete taustateadmiste lisamine mudelisse aitab vältida mudelite üle-fittimist.
Järeldused ühe hüpoteesi kohta mõjutavad järeldusi ka kõikide alternatiivsete hüpoteeside kohta. Relevantsete hüpoteeside eiramine viib ekslikele järeldustele kõigi teiste hüpoteeside kohta. Me ei saa põhimõtteliselt rääkida tõendusmaterjali tugevusest ühe hüpoteesi kontekstis – tõendusmaterjal on suhteline ja selle tugevust mõõdab tõepärade suhe \(P(andmed~\vert~ H_1)/P(andmed ~ \vert ~H_2)\).

Andmed ei ole sama, mis tegelikkus

Nüüd, kus me saame aru tõenäosusteooriast, on aeg asuda statistika kallale. Me ei kasuta statistikat vabatahtlikult, vaid teeme seda ainult siis, kui usume kahte asja: ühest küljest, et meie andmed on piisavalt tõetruud, et nende põhjal saaks teha adekvaatseid oletusi päris maailma kohta. Ja teisest küljest, et meie andmed ei ole piisavalt tõetruud, et neid järeldusi saaks teha lihtsalt ja intuitiivselt. Seega tasub alustada näitega sellest, kuidas andmed ja tegelikkus erinevad. Meie tööriistaks on siin simulatsioon. Simuleerimine on lahe, sest simulatsioonid elavad mudeli väikeses maailmas, kus me teame täpselt, mida me teeme ja mida on selle tagajärjel oodata. Simulatsioonidega saame hõlpsalt kontrollida, kas ja kuidas meie mudelid töötavad, aga ka genereerida olukordi (parameetrite väärtuste kombinatsioone), mida suures maailmas kunagi ette ei tule. Selles mõttes on mudelid korraga nii väiksemad kui suuremad kui päris maailm.

Alustuseks simuleerime juhuvalimi n = 3 lõpmata suurest normaaljaotusega populatsioonist, mille keskmine on 100 ja sd on 20. See on põhimõtteliselt sama simulatsioon, millise me tegime eelnevalt peatükis “Normaaljaotuse mudel väikestel valimitel”. Jällegi, tähtis ei ole konkreetne juhuvalim, vaid valimi erinevus populatsioonist. Päriselus on korraliku juhuvalimi saamine tehniliselt raske ettevõtmine ja, mis veelgi olulisem, me ei tea kunagi, milline on populatsiooni tõeline jaotus, keskmine ja sd. Seega, elagu simulatsioon!

set.seed(1) # makes random number generation reproducible
Sample <- rnorm(n = 3, mean = 100, sd = 20)
Sample; mean(Sample); sd(Sample)
#> [1]  87.5 103.7  83.3
#> [1] 91.5
#> [1] 10.8

Nagu näha on meie konkreetse valimi keskmine 10% väiksem kui peaks ja valimi sd lausa kaks korda väiksem. Seega peegeldab meie valim halvasti populatsiooni — aga me teame seda ainult tänu sellele, et tegu on simulatsiooniga.

Kui juba simuleerida, siis robinal: tõmbame ühe juhuvalimi asemel 10 000, arvutame seejärel 10 000 keskmist ja 10 000 sd-d ning vaatame nende statistikute jaotusi ja keskväärtusi. Simulatsioon on nagu tselluliit — see on nii odav, et igaüks võib seda endale lubada.

Meie lootus on, et kui meil on palju valimeid, millel kõigil on juhuslik viga, mis neid populatsiooni suhtes ühele või teisele poole kallutab, siis rohkem on valimeid, mis asuvad tõelisele populatsioonile pigem lähemal kui kaugemal. Samuti, kui valimiviga on juhuslik, siis satub umbkaudu sama palju valimeid tõelisest populatsiooniväärtusest ühele poole kui teisele poole ja vigade jaotus tuleb sümmeetriline.

N <- 3
N_simulations <- 10000
df <- tibble(a = rnorm(N * N_simulations, 100, 20), 
             b = rep(1:N_simulations, each = N))
Summary <-  df %>% 
  group_by(b) %>% 
  summarise(Mean = mean(a), SD = sd(a)) 
Summary %>% 
  ggplot(aes(Mean)) + 
  geom_histogram(bins = 40)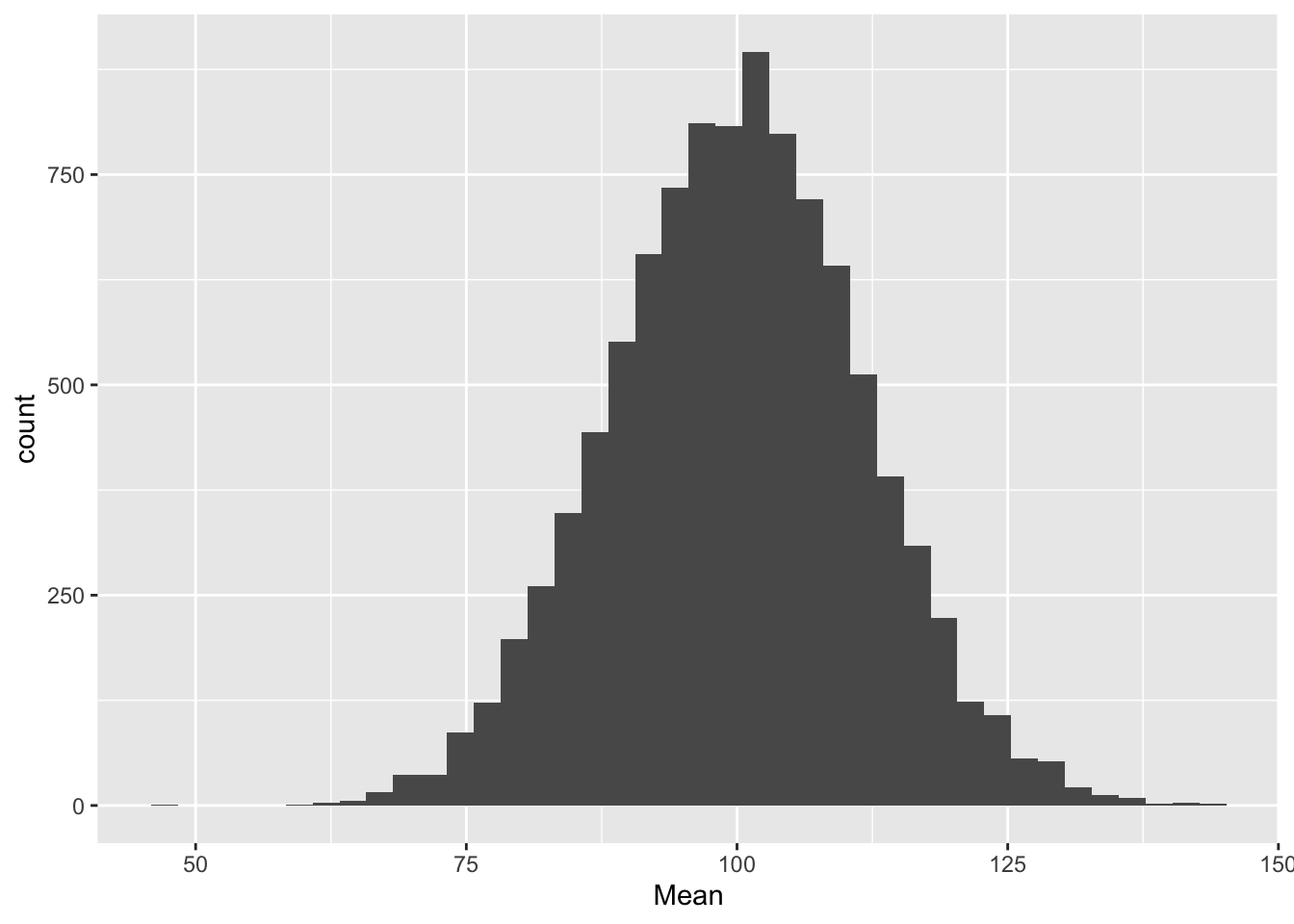

Joonis 11.1: Keskmiste jaotus 10 000 valimist.

mean(Summary$Mean) 
#> [1] 100
mean(Summary$SD)
#> [1] 17.8

Oh-hooo. Paljude valimite keskmiste keskmine ennustab väga täpselt populatsiooni keskmist aga sd-de keskmise keskmine alahindab populatsiooni sd-d. Valem, millega sd-d arvutatakse, töötab lihtsalt kallutatult, kui n on väike (<10). Kes ei usu, kordab simulatsiooni valimiga, mille N=30.

Ja nüüd 10 000 SD keskväärtused:

Summary %>% 
  ggplot(aes(SD)) + 
  geom_histogram(bins = 40)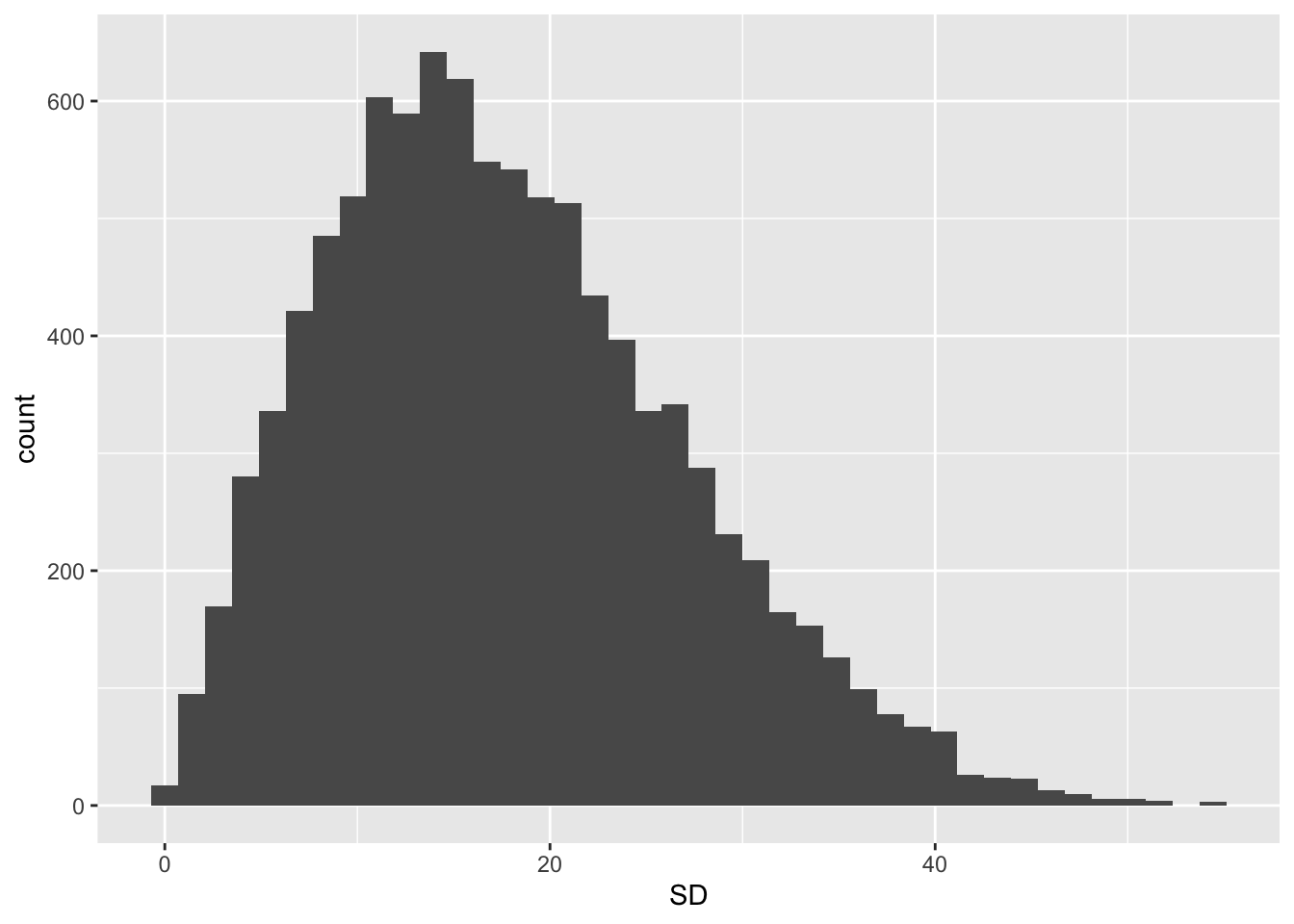

Joonis 11.2: SD-de jaotus 10 000 valimist.

mode <- function(x, adjust = 1){
  x <- na.omit(x)
  dx <- density(x, adjust = adjust)
  dx$x[which.max(dx$y)]
}
mode(Summary$SD) 
#> [1] 14.1

SD-de jaotus on ebasümmeetriline ja mood ehk kõige tõenäolisem valimi sd väärtus, mida võiksime oodata, on u 14, samal ajal kui populatsiooni sd = 20. Lisaks alahinnatud keskmisele sd-le on sd-de jaotusel paks saba, mis tagab, et teisest küljest pole ka vähetõenäoline, et meie valimi sd populatsiooni sd-d kõvasti üle hindab.

Arvutame, mitu % valimite sd-e keskmistest on > 25

mean(Summary$SD > 25)
#> [1] 0.211

Me saame >20% tõenäosusega pahasti ülehinnatud SD.

mean(Summary$SD < 15)
#> [1] 0.434

Ja me saame >40% tõenäosusega pahasti alahinnatud sd. Selline on väikeste valimite traagika.

Aga vähemalt populatsiooni keskmise saame me palju valimeid tõmmates ilusasti kätte — ka väga väikeste valimitega.

Kahjuks pole meil ei vahendeid ega kannatust loodusest 10 000 valimi kogumiseks. Enamasti on meil üksainus valim. Õnneks pole sellest väga hullu, sest meil on olemas analoogne meetod, mis töötab üsna hästi ka ühe valimiga. Me teeme lihtsalt ühest valimist mitu, mis meenutab pisut mittemillegist midagi tegemist, aga veidi üllatuslikult töötab selles kontekstis üsna hästi. Seda metoodikat kutsutakse bootstrappimiseks ja selle võttis esimesena kasutusele parun von Münchausen. Too jutukas parun nimelt suutis end soomülkast iseenda patsi pidi välja tõmmata (koos hobusega), mis ongi bootstrappimise põhimõte. (Inglise kultuuriruumis tõmbab bootstrappija ennast mülkast välja oma saapaserva pidi – siit ka meetodi nimi.) Statistika tõmbas oma saapaid pidi mülkast välja Brad Efron 1979. aastal.

Nii nagu parun Münchausen tõmbas ennast patsi pidi mülkast välja, genereeritakse bootstrappimisega algse valimi põhjal teststatistiku jaotus.

Joonis 11.3: Nii nagu parun Münchausen tõmbas ennast patsi pidi mülkast välja, genereeritakse bootstrappimisega algse valimi põhjal teststatistiku jaotus.