19 Keerulisemate mudelitega töötamine

library(tidyverse)
library(gapminder)
library(rethinking)
library(bayesplot)
library(gridExtra)

Kasuta graafilisi meetodeid. Mudeli koefitsientide jõllitamine üksi ei päästa.

g2007 <- gapminder %>% 
  filter(year == 2007)
g2007 <- g2007 %>% 
  mutate(l_GDP = log10(gdpPercap),
         l_pop = log10(pop), 
         lpop_s = (l_pop - mean(l_pop )) / sd(l_pop),
         lGDP_s = (l_GDP - mean(l_GDP )) / sd(l_GDP)) %>% 
  as.data.frame()

Predictor residual plots

m5 <- map2stan(
    alist(
        lifeExp ~ dnorm( mu , sigma ) ,
        mu <- a + b_GDP * lGDP_s + b_pop * lpop_s ,
        a ~ dnorm( 0 , 10 ) ,
        c(b_GDP, b_pop) ~ dnorm( 0 , 1 ) ,
        sigma ~ dunif( 0 , 10 )
), data = g2007 )

Plotime varieeruvuse, mida mudel ei oota ega seleta.

names(coef(m5))
#> [1] "a"     "b_GDP" "b_pop" "sigma"

Kõigepealt lihtne residuaalide plot, kus meil on y-teljel residuaalid ja x-teljel X1 muutuja tegelikud valimiväärtused. Y = 0 tähistab horisontaalse joonena mudeli ennustatud Y (eluea) väärtusi kõigil prediktori X1 (lGDP_s) väärtustel ja residuaal on defineeritud kui tegelik Y miinus mudeli poolt ennustatud eluiga sellel X1 väärtusel. Mudeli ennustuse saamiseks anname mudelile ette fikseeritud parameetrite (koefitsientide) a, b_GDP ja b_pop väärtused ning arvutame oodatava keskmise eluea üle kõigi valimis leiduvate lGDP_s ja lpop_s väärtuste. Seega saame sama palju keskmise eluea ennustusi, kui palju on meie andmetabelis ridu.

# Using the fitted model compute the expected value of y (mu) 
# for each of the 142 data rows.
mu <- coef(m5)['a'] + 
  coef(m5)['b_GDP'] * g2007$lGDP_s + 
  coef(m5)['b_pop'] * g2007$lpop_s

# compute residuals - a vector w. 142 values
m.resid <- g2007$lifeExp - mu

ggplot( g2007, aes( lGDP_s, m.resid ) ) + 
  geom_segment( aes( xend = lGDP_s, yend = 0 ), size = 0.2 ) +
  geom_point( size = 0.5, type = 1 )
#> Warning: Ignoring unknown parameters: type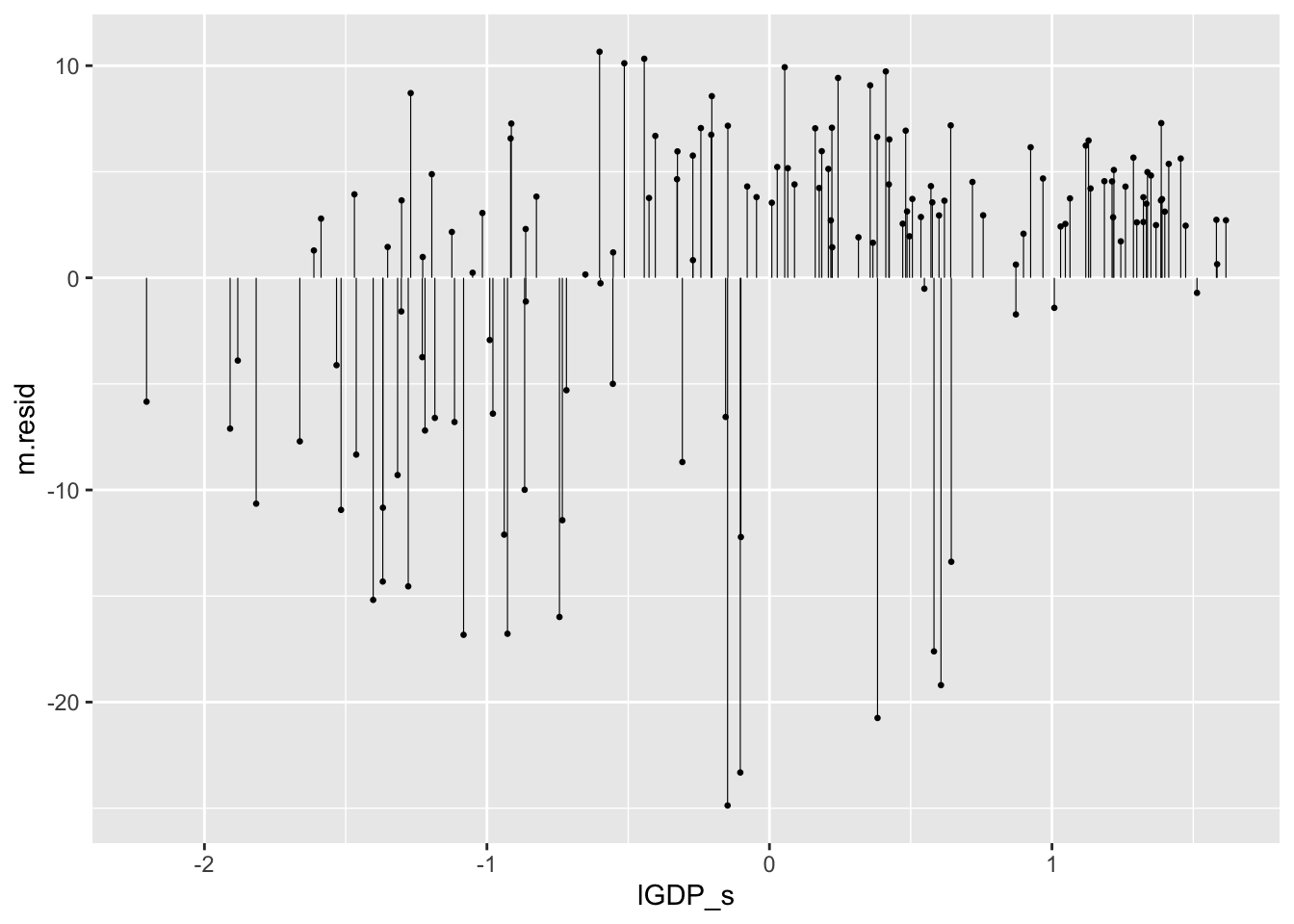

Joonis 4.3: Mudeli residuaalide plot (m.resid ~ X1).

Me näeme, et seal kus SKP on väiksem kipuvad residuaalid olema negatiivsed, mis tähendab, et mudel ülehindab keskmist eluiga. Ja vastupidi, seal kus SKP on üle keskmise, mudel kipub alahindma keskmist eluiga.

See seos tuleb eriti selgelt välja järgmisel pildil, kus plotime residuaalide sõltuvuse elueast (kui eelmine plot oli m.resid ~ X1, siis nüüd plotime m.resid ~ Y). Lisaks joonistame selguse mõttes regressioonisirge. Kui residuaalid oleks ühtlaselt jaotunud mõlemale poole mudeli ennustust, siis saaksime horisontaalse regressioonisirge. Tegeliku sirge tõus näitab, et suuremad eluead omavad eelistatult poitiivseid residuaale ja väiksemad eluead negatiivseid residuaale. See tähendab, et mudel alahindab eluiga seal, kus SKP on kõrge ja vastupidi, ülehindab eluiga seal, kus SKP on madal.

g2007$m.resid <- m.resid
ggplot(g2007, aes(lifeExp, m.resid)) +
  geom_smooth(method = "lm", se = FALSE) +
  geom_point() +
  geom_hline(yintercept = 0, color = "grey", linetype = 2)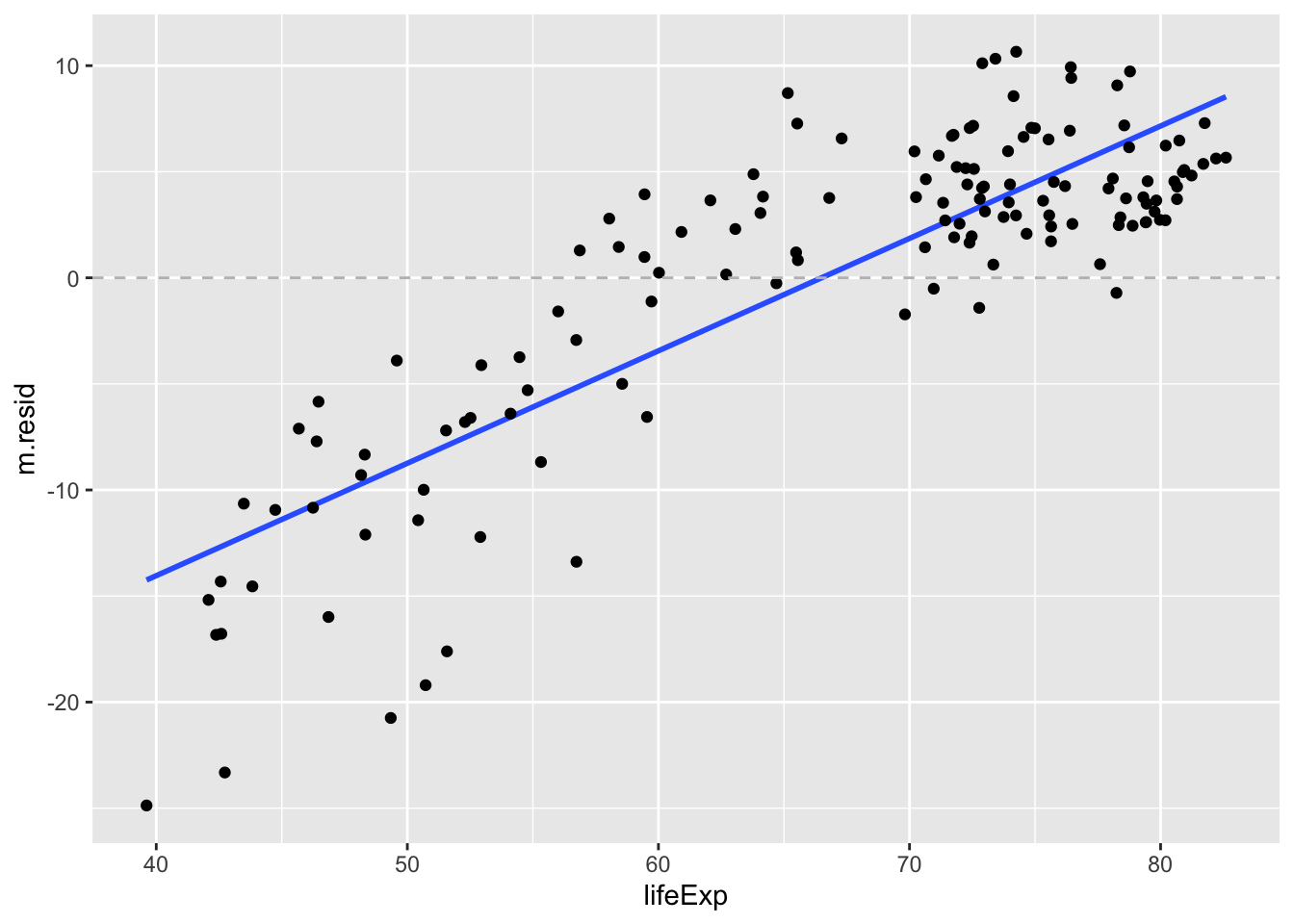

Joonis 19.1: m.resid ~ Y plot

Horisontaalne punktiirjoon näitab, kus mudel vastab täpselt andmetele.

Ennustavad plotid

Plot, kus me ennustame keskmise eluea sõltuvust SKP-st nii riikide kaupa eraldi (andmepunktide paupa) kui üldiselt kõikide riikide keskmisena, millel on mingi kindel SKP (mudeli parima ennustuse ehk sirge asendi ümber valitsevat ebakindlust). Et seda teha, hoiame rahvaarvu konstantsena oma keskväärtusel, mis standardiseeritud andmetl võrdub alati nulliga. link() funktsioon annab meile keskmiste eluigade ennustused meie poolt ette antud X1 ja X2 väärtustel, ning sim() annab meile eluigade ennustused fiktsionaalsete riikide kaupa samadel X1 ja X2 väärtustel. Nagu näha, on meie mudeli arvates riikide kaupa ennustamine palju laiema varieeruvusega kui üle kõikväimalike riikide kesmise kaupa ennustamine.

# prepare new counterfactual data
pred.data <- tibble(
    lGDP_s = seq(-3, 3, length.out = 30), # need meie poolt valitud lGDP_s väärtused, millele me ennustame vastavad eluead 
    lpop_s = 0 # rahvaarv fikseeritakse muutuja keskmisele tasemele, mis standardiseeritud andmete korral = 0
)

# compute counterfactual mean lifeExp (mu)
mu <- link(m5, data = pred.data)
#> [ 100 / 1000 ]
[ 200 / 1000 ]
[ 300 / 1000 ]
[ 400 / 1000 ]
[ 500 / 1000 ]
[ 600 / 1000 ]
[ 700 / 1000 ]
[ 800 / 1000 ]
[ 900 / 1000 ]
[ 1000 / 1000 ]
mu.mean <- apply(mu, 2, mean)
mu.PI <- apply(mu, 2, PI)

# simulate counterfactual lifeExpectancies of individual countries
R.sim <- sim(m5, data = pred.data)
#> [ 100 / 1000 ]
[ 200 / 1000 ]
[ 300 / 1000 ]
[ 400 / 1000 ]
[ 500 / 1000 ]
[ 600 / 1000 ]
[ 700 / 1000 ]
[ 800 / 1000 ]
[ 900 / 1000 ]
[ 1000 / 1000 ]
R.sim <- na.omit(R.sim)
R.PI <- apply(R.sim, 2, PI)
pred.data$mu.mean <- mu.mean
pred.data$lower <- mu.PI[1,]
pred.data$upper <- mu.PI[2,]
pred.data$lower1 <- R.PI[1,]
pred.data$upper1 <- R.PI[2,]

ggplot(pred.data, aes(lGDP_s, mu.mean)) +
  geom_line() +
  geom_ribbon(aes(ymin = lower, ymax = upper), fill = "grey60", alpha = 0.3) +
  geom_ribbon(aes(ymin = lower1, ymax = upper1), fill = "grey10", alpha = 0.3)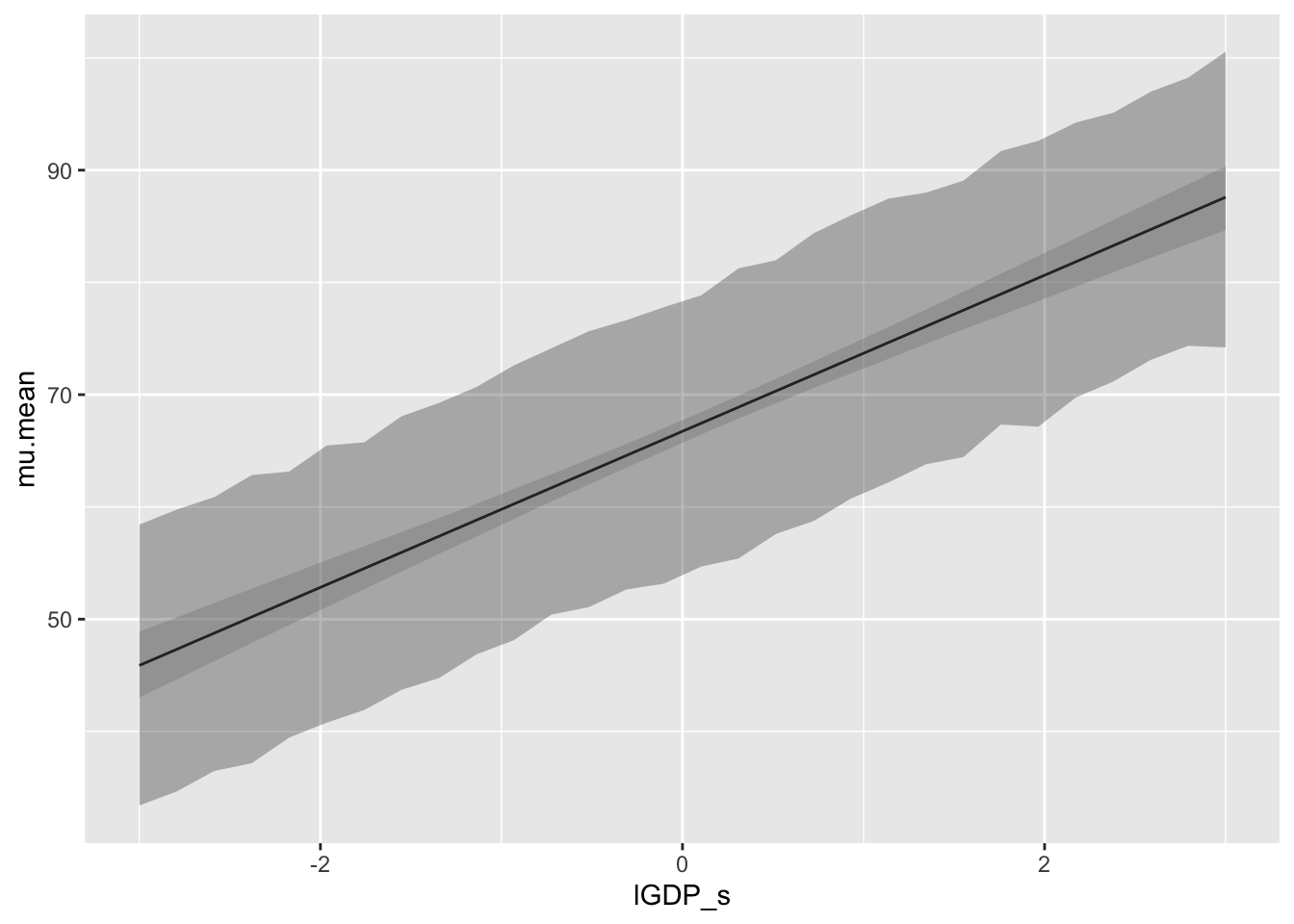

Joonis 4.4: Ennustav plot

Näeme, kuidas ennustus sobib/ei sobi andmetega. Võrdle eelneva ennustuspildiga, kus mudel ei sisalda rahvaarvu. Ennustuse intervallid on originaalandmete skaalas (aastates), mis on hea.

Posterior prediction plots

Posterioorsed ennustusplotid panevad kõrvuti (või üksteise otsa) Y-i algandmed ja mudeli ennustused Y-väärtustele. Kui meie valimi suurus on N, siis me tõmbame mudelist näiteks 5 valimit, igaüks suurusega N ja plotime need kõrvuti valimiandmete plotiga. Siis me vaatame sellele plotile peale ja otsustame, kas mudeli ennustused on piisavalt lähedal valimi andmetele. Kui ei, siis on tõenäoline, et meie mudelis on midagi mäda ja me peame hakkama sealt vigu otsima. Tõsi küll, keerulisemate hierarhiliste mudelite korral on vahest raske otsustada, millised peaksid tulema eduka mudeli ennustused võrreldes algandmetega — aga siiski, see on arvatavasti kõige tähtsam plot, mida oma mudelist teha!

võrdle mudeli ennustusi andmetega. (Aga arvesta sellega, et mitte kõik mudelid ei püüagi täpselt andmetele vastata.)

yrep <- sim(m5)
#> [ 100 / 1000 ]
[ 200 / 1000 ]
[ 300 / 1000 ]
[ 400 / 1000 ]
[ 500 / 1000 ]
[ 600 / 1000 ]
[ 700 / 1000 ]
[ 800 / 1000 ]
[ 900 / 1000 ]
[ 1000 / 1000 ]
ppc_dens(g2007$lifeExp, yrep[1:5, ])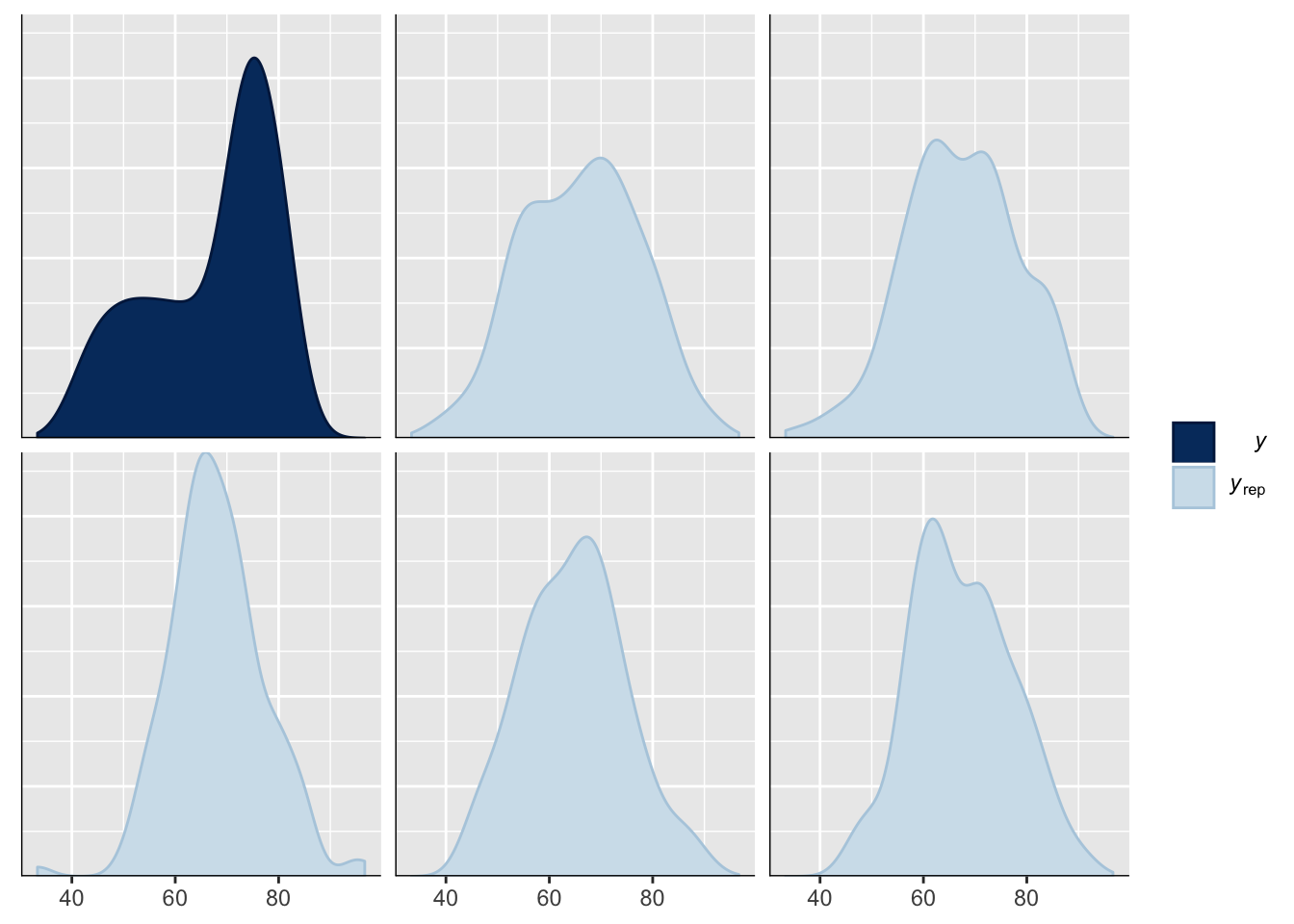

Joonis 19.2: Valimi andmed vs. mudeli poolt ennustatud andmed.

Millisel viisil täpselt meie mudel ebaõnnestub? See plot annab mõtteid, kuidas mudelit parandada.

Ploti ennustused andmepunktide vastu, pluss jooned, mis näitavad igale ennustusele omistatud usaldusintervalli. Lisaks veel sirge, mis näitab täiuslikku ennustust (slope = 1, intercept = 0).

Ja nüüd plotime ennustused Y-le tegelike Y valimi väärtuste vastu:

mu <- link(m5)  
#> [ 100 / 1000 ]
[ 200 / 1000 ]
[ 300 / 1000 ]
[ 400 / 1000 ]
[ 500 / 1000 ]
[ 600 / 1000 ]
[ 700 / 1000 ]
[ 800 / 1000 ]
[ 900 / 1000 ]
[ 1000 / 1000 ]
mu.mean <- apply(mu, 2, mean)

mu.PI <- apply(mu , 2 , PI)

g2007$mu.mean <- mu.mean

ggplot(g2007, aes(lifeExp, mu.mean)) +
  geom_point() +
  geom_crossbar(ymin = mu.PI[1,], ymax = mu.PI[2,]) +
  geom_abline(intercept = 0, slope = 1, lty = 2) +
  ylab("Predicted life expectancy") + 
  xlab("Observed life expectancy") +
  coord_cartesian( xlim=c( 40, 85 ), ylim=c( 40, 85 ))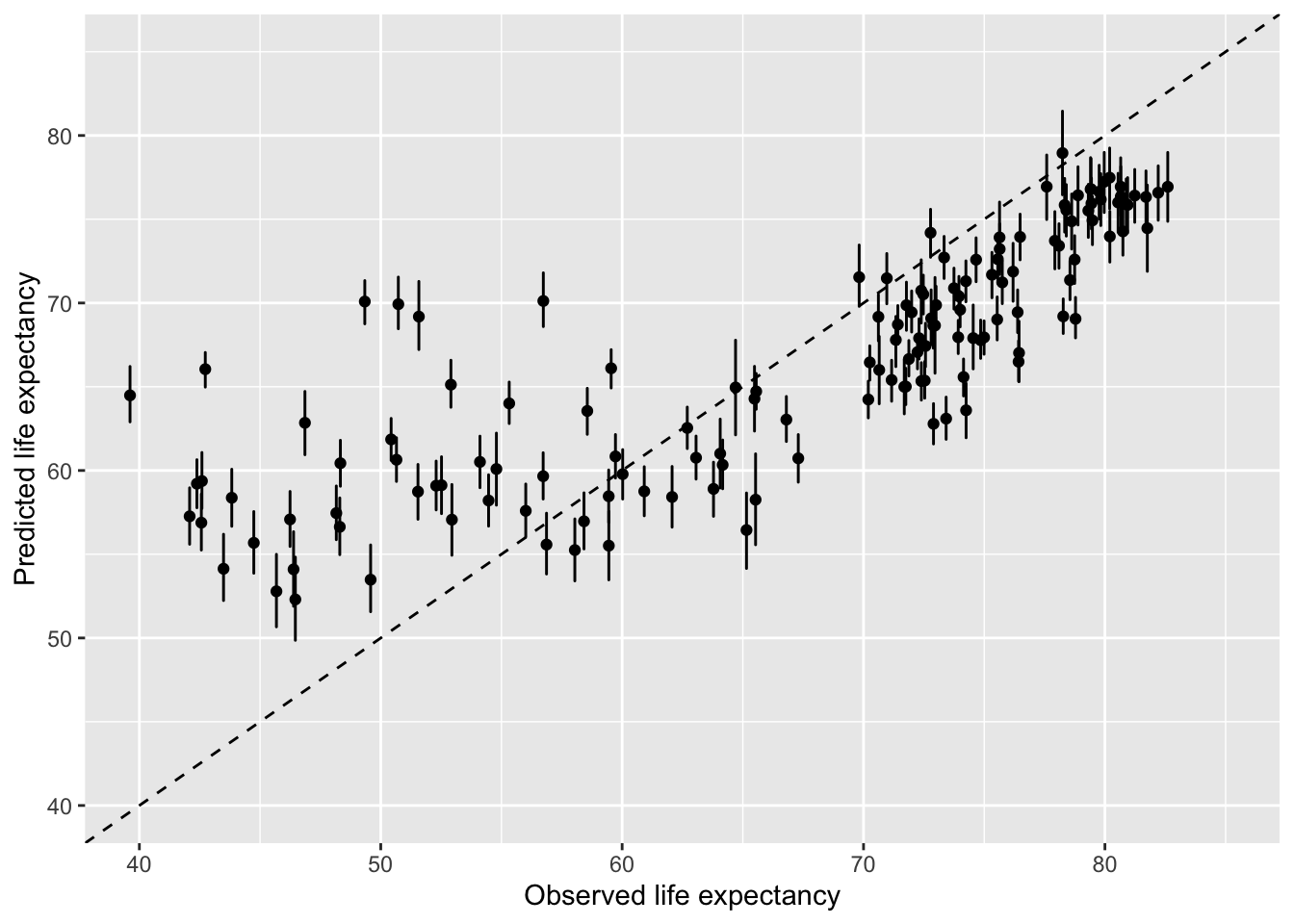

Joonis 4.5: Ennustus vs. valimi väärtus

Siin on ennustus ja seda ümbritsev ebakindlus iga riigi keskmisele elueale.

Järgnev plot annab ennustusvea igale riigile. Siin tähistab 89% CI näiteks Vietnamile eluigade vahemikku, millese jääb mudeli ennustuse kohaselt 89% kõikvõimalike fiktsionaalsete riikide keskmistest eluigadest, mille SKP ja rahvaarv võrdub Vietnami omaga. Kuna me tsentreerime CI Vietnami tegeliku keskmise eluea residuaalile (erinevusele mudeli ennustusest), näitab see, kui palju erineb Vietnami eluiga mudeli ennustusest riikidele, nagu Vietnam. See plot annab meile riigid, mille suhtes mudel jänni jääb. Enamasti leiame need riigid Aafrikast.

# compute residuals
life.resid <- g2007$lifeExp - mu.mean

mu_sim <- sim( m5 )  
#> [ 100 / 1000 ]
[ 200 / 1000 ]
[ 300 / 1000 ]
[ 400 / 1000 ]
[ 500 / 1000 ]
[ 600 / 1000 ]
[ 700 / 1000 ]
[ 800 / 1000 ]
[ 900 / 1000 ]
[ 1000 / 1000 ]
sim.PI <- apply( mu_sim , 2 , PI )

ggplot(g2007, aes(x = life.resid, y = reorder(country, life.resid))) +
  geom_point() +
  geom_errorbarh(aes(xmin = lifeExp - sim.PI[1,], 
                     xmax = lifeExp - sim.PI[2,] ), 
                  color = "red") +
  geom_vline(xintercept = 0) +
  theme(text = element_text(size = 7),
        axis.title.y = element_blank())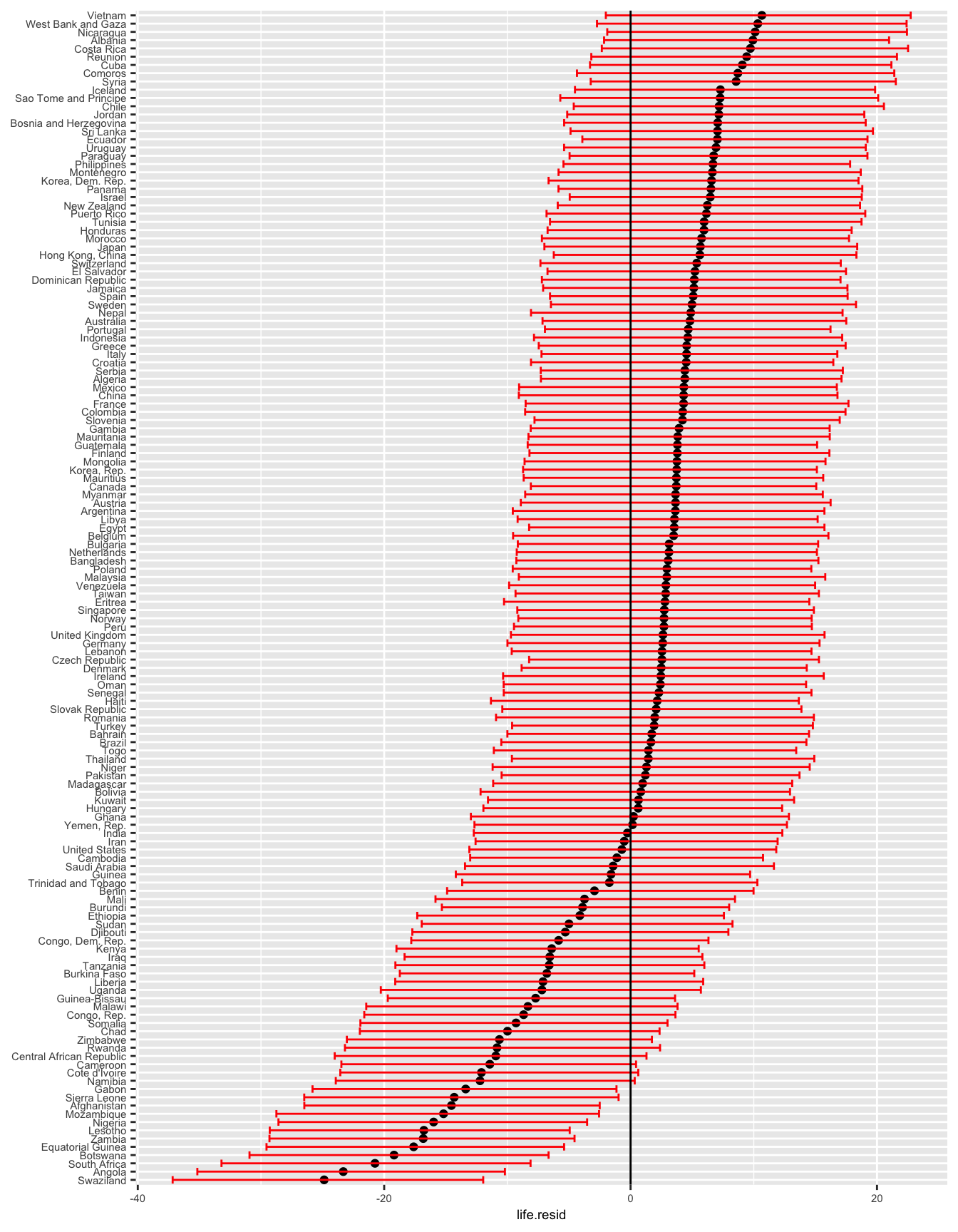

Joonis 16.7: Ennustused riigi kaupa.

punased jooned näitavad 89% ennustuspiire igale residuaalile riigi tasemel (89% kõikvõimalike riikide keskmiste eluigade residuaalidest sellel SKPl jääb punasesse vahemikku).

Interaktsioonid prediktorite vahel

Eelnevad mudelid eeldavad, et prediktorite varieeruvused on üksteisest sõltumatud. Aga mis siis, kui see nii ei ole ja ühe prediktori mõju suurus sõltub teisest prediktorist, ehk prediktorite vahel on interaktsioon? Lihtsaim viis sellist interaktsiooni modelleerida on lisades interaktsiooni aditiivsele mudelile korrutamisetehtena:

\(y = a + b1x1 + b2x2 + b3x1x2\)

Sellise mudeli järgi erineb sirge tõus b1 erinevatel b2 väärtustel, ja erinevuse määr sõltub b3-st (b3 annab interaktsiooni tugevuse). Samamoodi ja sümmeetriliselt erineb ka tõus b2 sõltuvalt b1 väärtusest. See on ühine paljude hierarhiliste mudelitega, mida võib omakorda vaadelda massivsete interaktsioonimudelitena. Seevastu y = a + b1x1 + b2x2 tüüpi mudel annab b1-le konstantse tõusunurga, kuid laseb intercepti muutuma sõltuvalt b2 väärtusest (ja vastupidi).

Interaktsioonimudeli fittimises pole midagi erilist võrreldes sellega, mida me oleme juba õppinud. Aga fititud parameetrite tõlgendamine on keeruline. Alustame diskreetse muutujaga, continent, ja mudeldame selle interaktsiooni SKP-ga.

f1 <- glimmer(lifeExp ~ lGDP_s * continent, data = g2007)
#> alist(
#>     lifeExp ~ dnorm( mu , sigma ),
#>     mu <- Intercept +
#>         b_lGDP_s*lGDP_s +
#>         b_continentAmericas*continentAmericas +
#>         b_continentAsia*continentAsia +
#>         b_continentEurope*continentEurope +
#>         b_continentOceania*continentOceania +
#>         b_lGDP_s_X_continentAmericas*lGDP_s_X_continentAmericas +
#>         b_lGDP_s_X_continentAsia*lGDP_s_X_continentAsia +
#>         b_lGDP_s_X_continentEurope*lGDP_s_X_continentEurope +
#>         b_lGDP_s_X_continentOceania*lGDP_s_X_continentOceania,
#>     Intercept ~ dnorm(0,10),
#>     b_lGDP_s ~ dnorm(0,10),
#>     b_continentAmericas ~ dnorm(0,10),
#>     b_continentAsia ~ dnorm(0,10),
#>     b_continentEurope ~ dnorm(0,10),
#>     b_continentOceania ~ dnorm(0,10),
#>     b_lGDP_s_X_continentAmericas ~ dnorm(0,10),
#>     b_lGDP_s_X_continentAsia ~ dnorm(0,10),
#>     b_lGDP_s_X_continentEurope ~ dnorm(0,10),
#>     b_lGDP_s_X_continentOceania ~ dnorm(0,10),
#>     sigma ~ dcauchy(0,2)
#> )

m1 <- map2stan(f1$f, f1$d)

plot(precis(m1))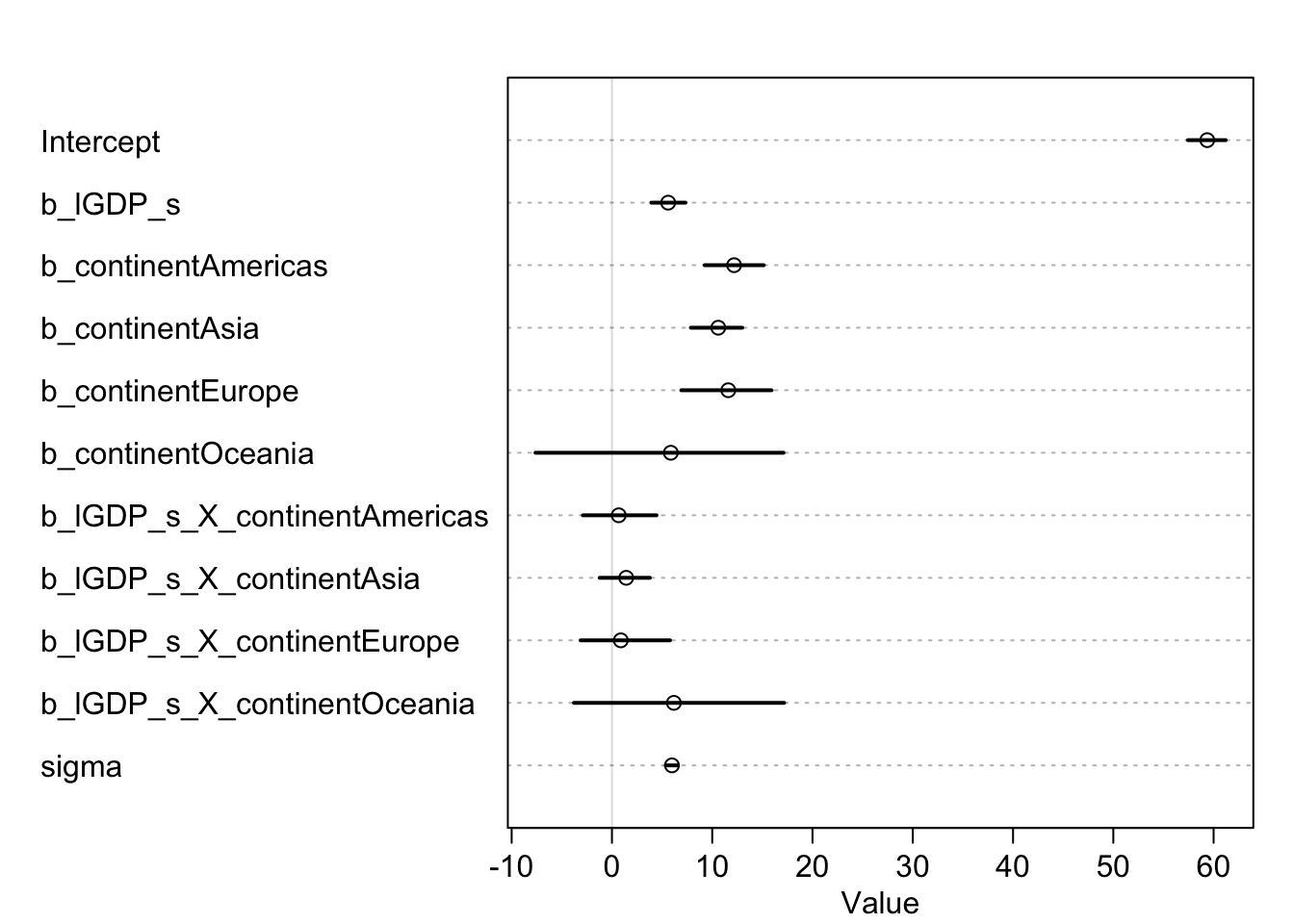

Joonis 4.7: Mudeli koefitsientide plot.

Aafrika on siin võrdluseks.

Interaktsioon on sümmeetriline. Me võime sama hästi küsida, kui palju SKP mõju elueale sõltub kontinendist, kui seda, kui palju kontinendi mõju eluale sõltub SKP-st.

Nüüd joonistame välja regressioonisirge Aafrika ja Euroopa jaoks eraldi m1 mudeli põhjal

c1 <- coef(m1)
names(c1)
#>  [1] "Intercept"                    "b_lGDP_s"                    
#>  [3] "b_continentAmericas"          "b_continentAsia"             
#>  [5] "b_continentEurope"            "b_continentOceania"          
#>  [7] "b_lGDP_s_X_continentAmericas" "b_lGDP_s_X_continentAsia"    
#>  [9] "b_lGDP_s_X_continentEurope"   "b_lGDP_s_X_continentOceania" 
#> [11] "sigma"

Kõigepealt defineerime X1 ja X2 väärtused, millele teeme ennustused link() funktsiooni abil. Link tabelist veergude keskmine annab keskmise eluea ennustuse vastavale mandrile ja SKP-le. PI() abil saame 89% CI igale ennustusele.

dd <- as.data.frame(f1$d) #we use the dataframe made by glimmer()
#in dd all continents are in separate 2-level columns (except Africa)
dd1 <- dd %>% filter(continentAmericas == 0, 
                     continentAsia == 0, 
                     continentEurope == 0, 
                     continentOceania == 0)
mu.Africa <- link(m1, dd1)
#> [ 100 / 1000 ]
[ 200 / 1000 ]
[ 300 / 1000 ]
[ 400 / 1000 ]
[ 500 / 1000 ]
[ 600 / 1000 ]
[ 700 / 1000 ]
[ 800 / 1000 ]
[ 900 / 1000 ]
[ 1000 / 1000 ]
mu.Africa.mean <- apply(mu.Africa, 2, mean)
mu.Africa.PI <- apply(mu.Africa, 2, PI, prob = 0.9)

ggplot(dd1, aes(lGDP_s, lifeExp)) +
  geom_point() +
  geom_ribbon(aes(ymin = mu.Africa.PI[1,], ymax = mu.Africa.PI[2,]), alpha = 0.15) +
  geom_line(aes(y = mu.Africa.mean))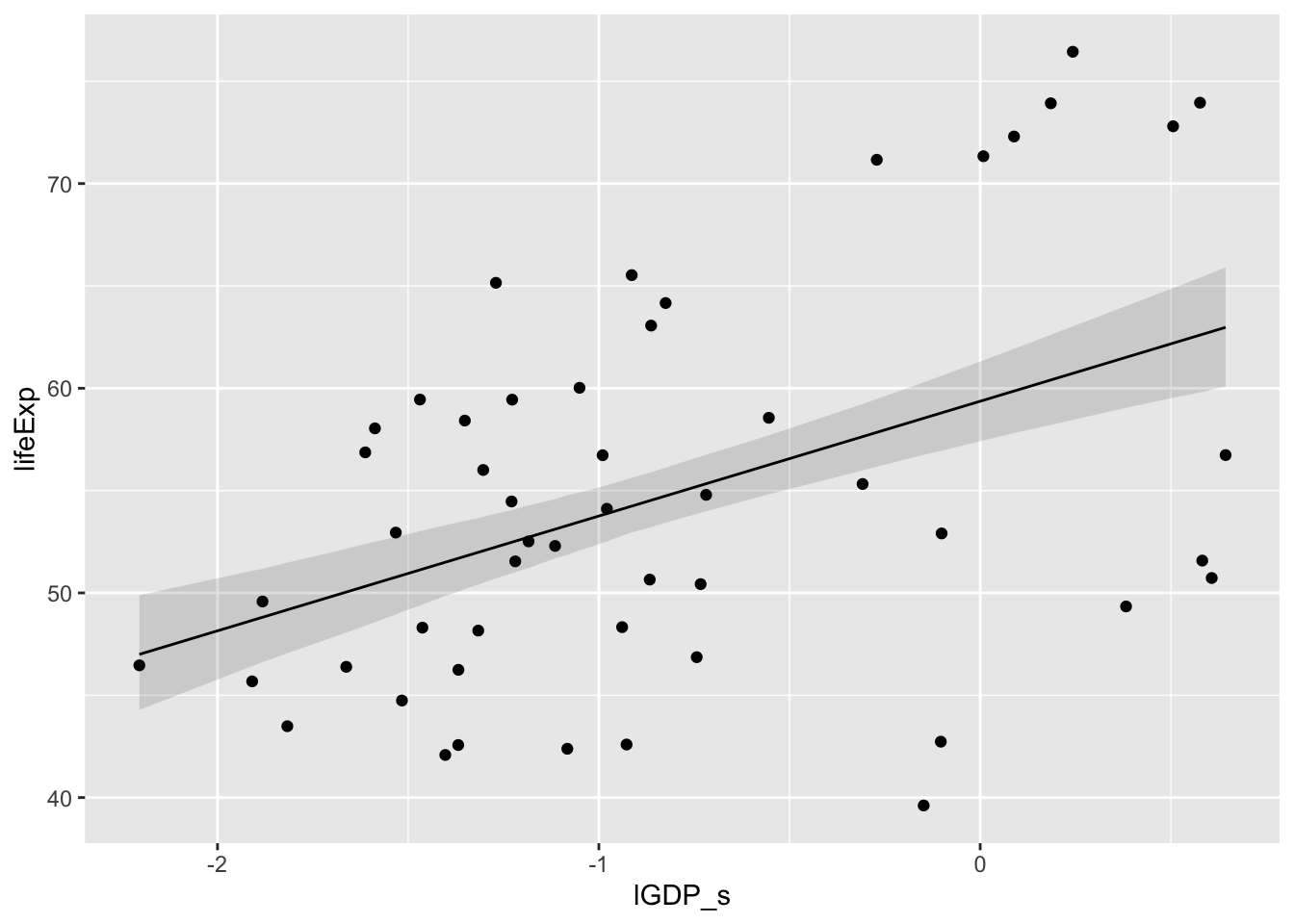

Joonis 16.9: Ennustusplot Aafrikale.

dd1 <- dd %>% filter(continentEurope == 1)
mu.Europe <- link(m1, dd1)
#> [ 100 / 1000 ]
[ 200 / 1000 ]
[ 300 / 1000 ]
[ 400 / 1000 ]
[ 500 / 1000 ]
[ 600 / 1000 ]
[ 700 / 1000 ]
[ 800 / 1000 ]
[ 900 / 1000 ]
[ 1000 / 1000 ]
mu.Europe.mean <- apply( mu.Europe , 2 , mean )
mu.Europe.PI <- apply( mu.Europe , 2 , PI , prob=0.9 )

ggplot(data=dd1, aes(lGDP_s, lifeExp)) +
  geom_point()+
  geom_ribbon( aes(ymin=mu.Europe.PI[1,], ymax=mu.Europe.PI[2,]), alpha=0.15)+
  geom_line( aes( y=mu.Europe.mean))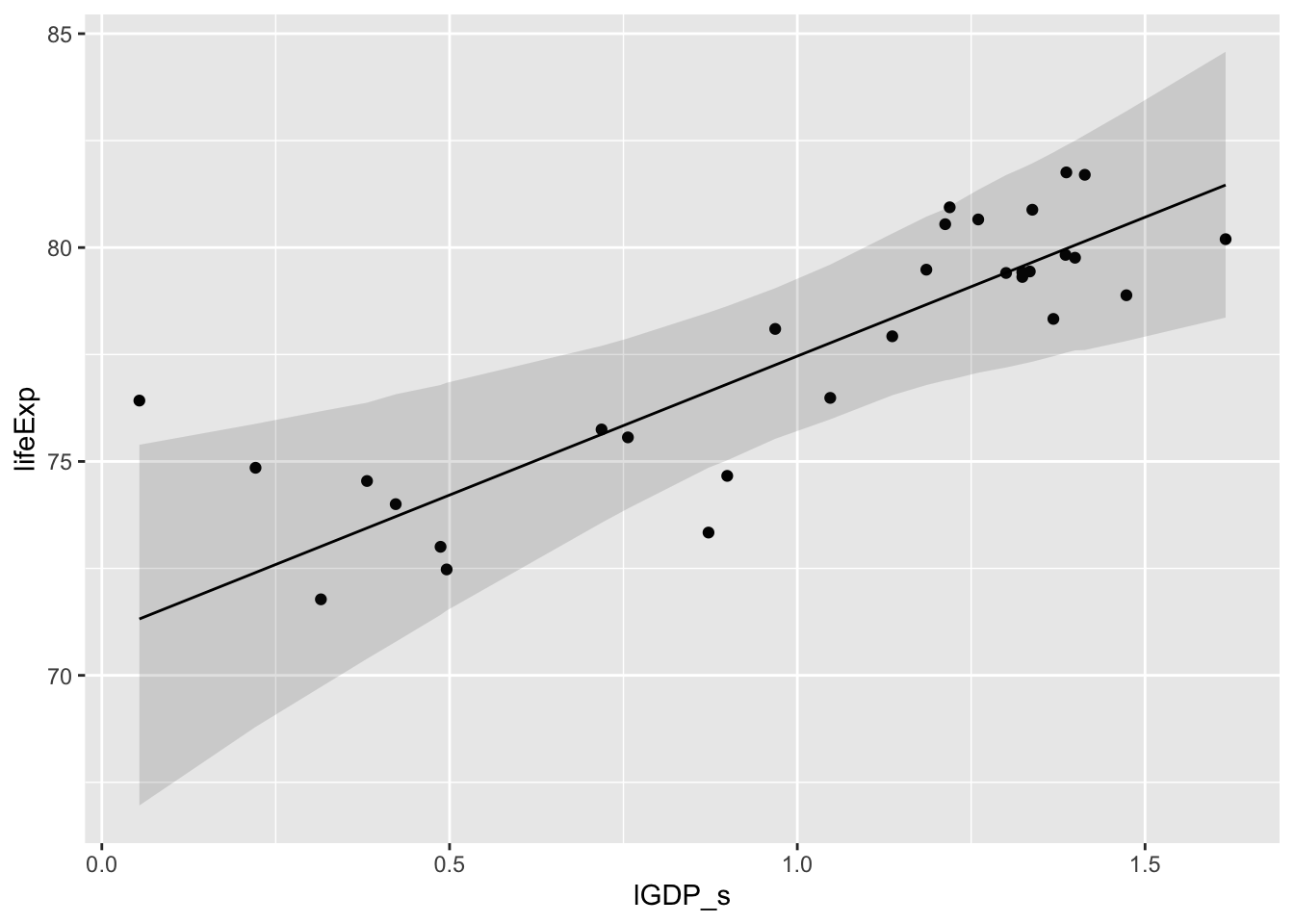

Joonis 16.10: Ennustusplot Euroopale.

Nagu näha, on meil nüüd üsna erinevad sirge tõusunurgad.

Interaktsioonid pidevatele tunnustele

Kasutame standardiseeritud prediktoreid, sest nende koefitsiente saab paremini tõlgendada (tegelikult piisab prediktorite tsentreerimisest). Meie andmed käsitlevad diabeedimarkereid Ameerika lõunaosariikide neegritel 1960-ndatel. Me ennustame siin sõltuvalt vanusest ja vööümbermõõdust hdl-i — high density cholesterol — mis on nn hea kolesterool.

diabetes <- read.csv2("data/diabetes.csv")
d1 <- diabetes %>% select(hdl, age, waist) %>% na.omit()
d2 <- d1 %>% mutate(age_st = (age - mean(age)) / sd(age), 
                    waist_st = (waist - mean(waist)) / sd(waist))

m2 <- map2stan(
    alist(
        hdl ~ dnorm( mu , sigma ) ,
        mu <- a + bR*age_st + bA*waist_st + bAR*age_st*waist_st,
        a ~ dnorm( 0, 100 ),
        bR ~ dnorm( 0, 2 ),
        bA ~ dnorm( 0, 2 ),
        bAR~ dnorm( 0, 2),
        sigma ~ dcauchy( 0, 1 )
), data = d2)

plot(precis(m2))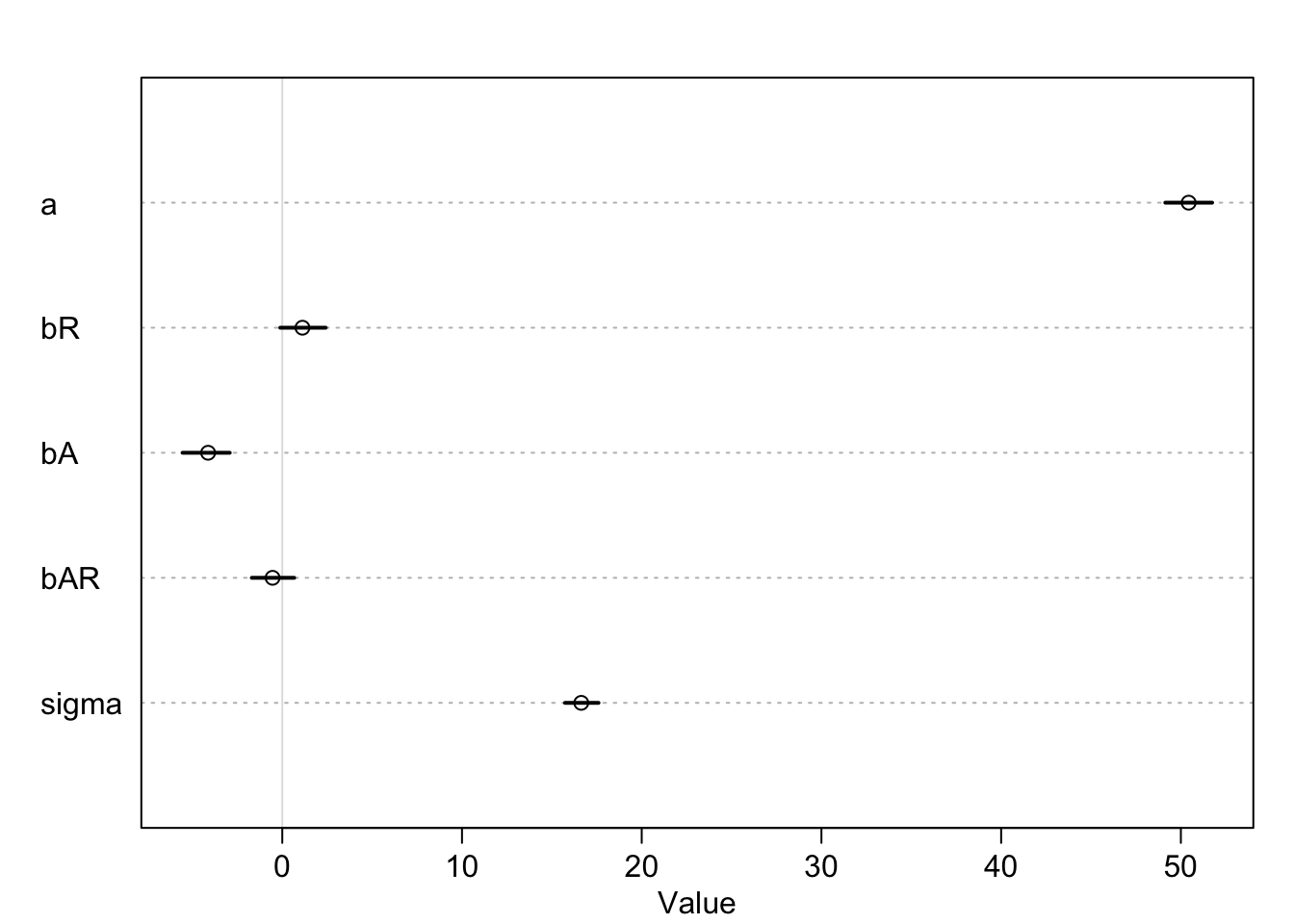

Joonis 19.3: mudeli koefitsientide plot

NB! Järgmised interpretatsioonid kehtivad ainult siis, kui mudeldame nullile tsentreeritud andmeid.

a - hdl-i oodatav keskväärtus siis kui võõ-ümbermõõt ja vanus on fikseeritud oma keskmistel väärtustel. bR - oodatav hdl-i muutus, kui vanus kasvab 1 aasta võrra ja võõ-ümbermõõt on fikseeritud oma keskväärtusel bA - sama, kui võõ-ümbermõõt kasvab 1 ühiku (inch) võrra bAR - kaks ekvivalentset tõlgendust: 1) oodatav muutus vanuse mõju määrale hdl-le, kui vöö-ümbermõõt kasvab 1 ühiku võrra. 2) oodatav muutus vöö-ümbermõõdu mõju määrale hdl-le, kui vanus kasvab 1 ühiku võrra.

Negatiivne bAR tähendab, et vanus ja vöö-ümbermõõt omavad vastandlikke mõjusid hdl-i tasemele, aga samas kumgki tõstab teise tähtsust hdl-le.

m3 <- map2stan(
    alist(
        hdl ~ dnorm(mu, sigma),
        mu <- a + bR * age_st + bA * waist_st,
        a ~ dnorm(0, 100),
        c(bR, bA) ~ dnorm(0, 2),
        sigma ~ dcauchy(0, 1)
), data = d2)

compare(m2, m3)
#>    WAIC pWAIC dWAIC weight   SE  dSE
#> m3 3391   5.6   0.0   0.72 41.8   NA
#> m2 3393   7.1   1.9   0.28 41.9 1.91

Siin on tegelikult eelistatud ilma interaktsioonita mudel. Aga kuna interaktsioonimudeli kaal on ikkagi 28%, tasub meil ennustuste tegemisel mõlemat mudelit koos arvestada vastavalt oma kaalule.

coeftab(m2, m3)
#>       m2      m3     
#> a        50.4    50.4
#> bR       1.12    1.09
#> bA      -4.13   -4.10
#> bAR     -0.54      NA
#> sigma    16.6    16.6
#> nobs      400     400

Tõesti, bA ja bR on mõlemas mudelis väga sarnased. m3 on kindlasti lihtsamini tõlgendatav.

Ensemble teeb ära nii link()-i kui sim()-i, kasutades mõlemat mudelit vastavalt nende mudelite WAIC-i kaaludele ja toodab listi, mille elementideks on link() toodetud maatriks ja sim() toodetud maatriks.

Teeme 3 plotti: waist = 0 (keskmine), waist = -1 (miinus üks sd) ja waist = 1

waist_fun <- function(waist, ...) {
  d.pred <- data.frame(age_st = seq( -2, 2, length.out = 20 ),
                       waist_st = waist)
  e <- ensemble(..., data = d.pred)
  hdl <- apply(e$link, 2, mean)
  mu.PI <- apply(e$link, 2, PI, prob = 0.97)
  ggplot(d.pred, aes(x = age_st)) +
    geom_line(aes(y = hdl)) +
    geom_line( aes(y = mu.PI[1,]), linetype = 2) +
    geom_line( aes( y = mu.PI[2,] ), linetype = 2) +
    ylim(40, 70)
}

Ensemble mudel:

## Fit ensemble model
# p <- lapply(-1:1, waist_fun, m2, m3)
## Plot three plots
# do.call(grid.arrange, c(p, ncol = 3))
## 
p_1 <- waist_fun(-1, m2, m3)
p0 <- waist_fun(0, m2, m3)
p1 <- waist_fun(1, m2, m3)
grid.arrange(p_1, p0, p1, ncol = 3)
#> Warning: Removed 2 rows containing missing values (geom_path).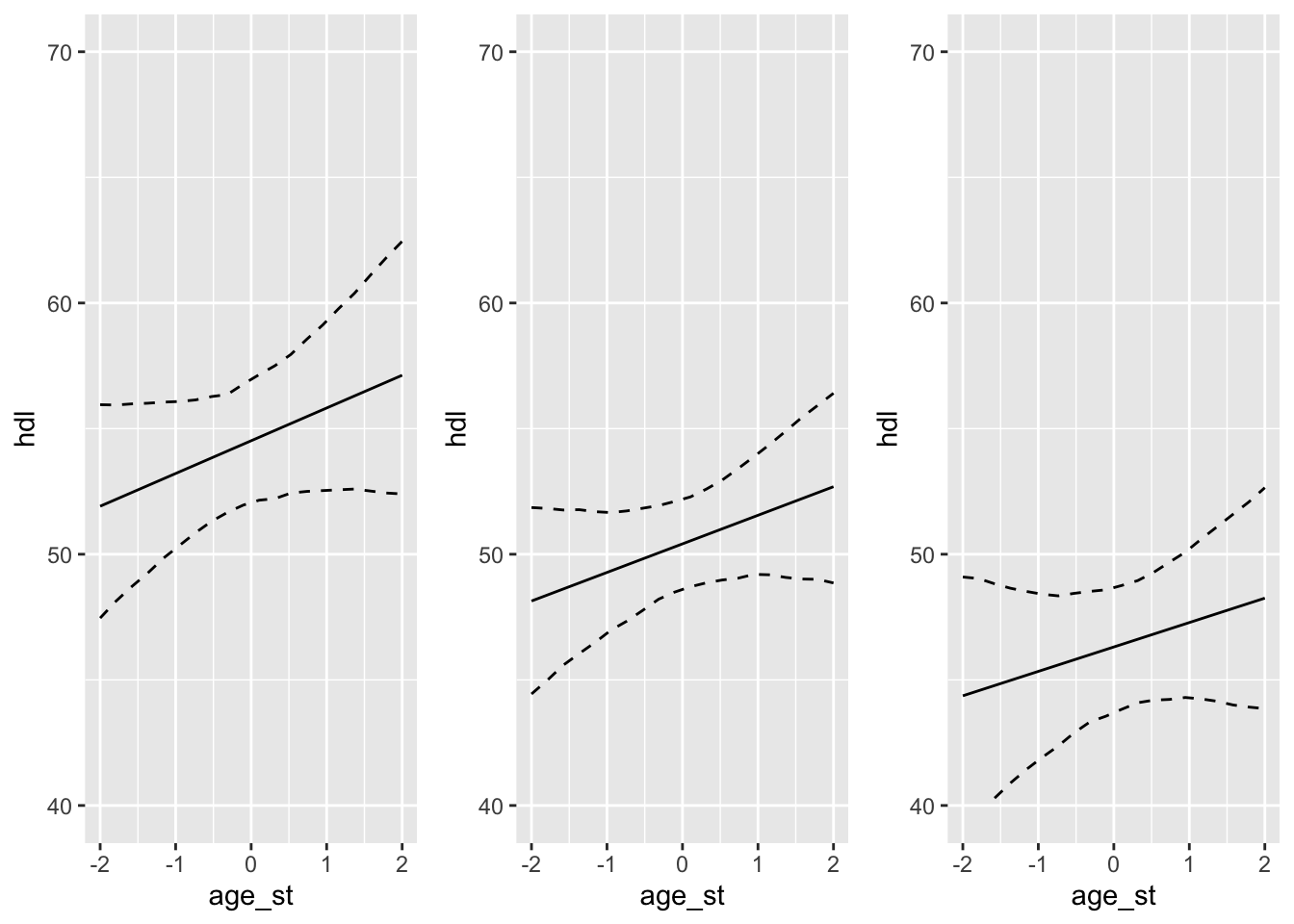

Joonis 19.4: Ennustusplot üle kahe mudeli.

Ja sama ainult ühe mudeliga – m2.

w0 <- waist_fun(-1, m2)
w_1 <- waist_fun(0, m2)
w1 <- waist_fun(1, m2)
grid.arrange(w0, w_1, w1, ncol = 3)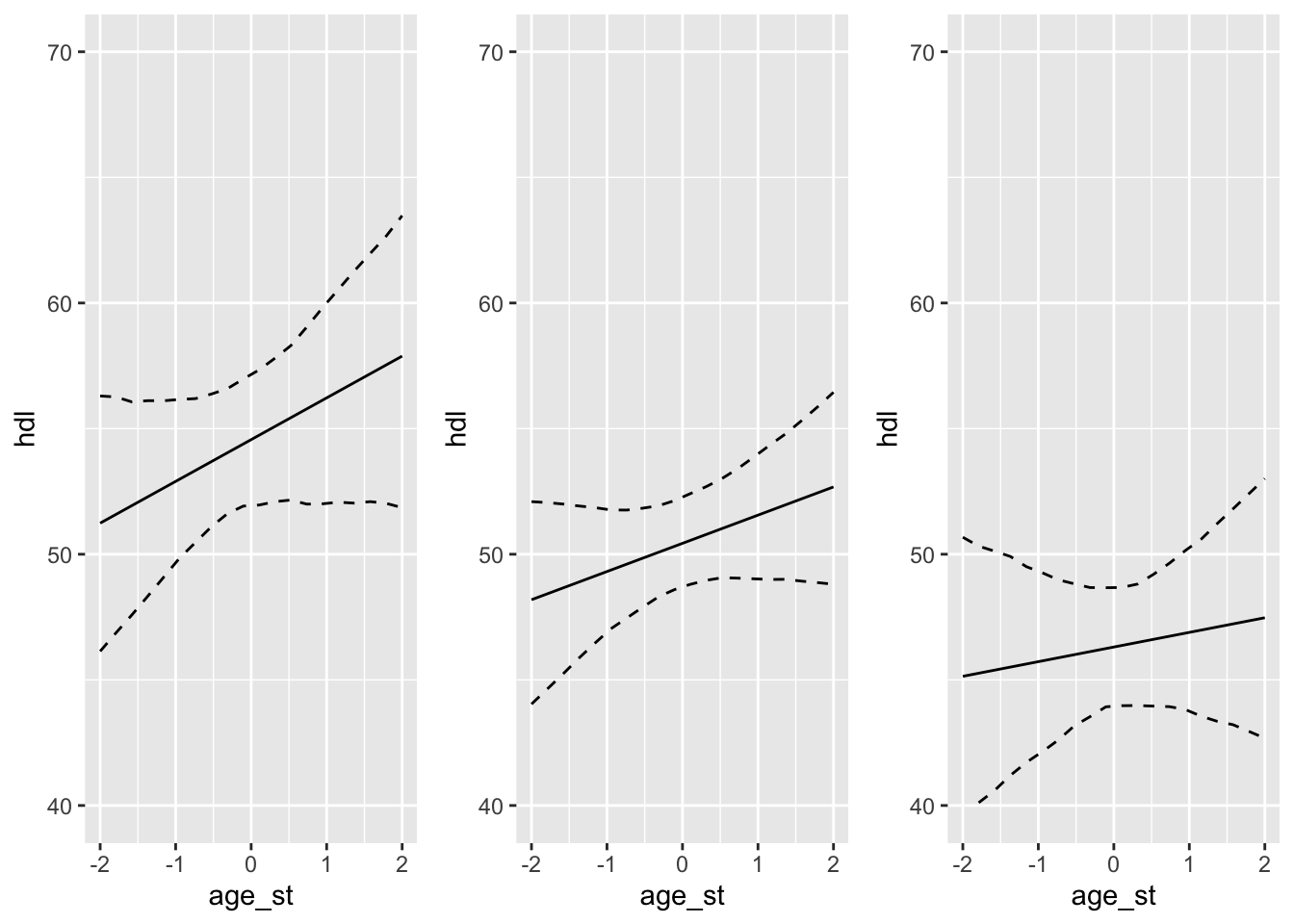

Joonis 16.11: Ennustusplot m2-le.

Nüüd on hästi näha, et interaktsioonimudel laseb sirge tõusunurgad vabaks!

Üldiselt tasub interaktsioon mudelisse sisse kirjutada siis, kui see interaktsioon on teoreetiliselt mõtekas (ühe prediktori mõju võiks sõltuda teise prediktori tasemest). Interaktsiooni koefitsiendi määramine võib suurendada ebakindlust teiste parameetrite määramisel, seda eriti siis kui interaktsiooni parameeter on korreleeritud oma komponentide parameetritega (vt pairs(model)).

Isegi kui interaktsiooniparameetri posteerior hõlmab 0-i, tuleb interaktsiooni parameetrit mudelisse pannes arvestada, et individuaalsete prediktorite mõju ei saa summeerida pelgalt läbi nende koefitsientide. Selle asemel tuleb vaadata sirge tõusu erinevatel teiste prediktorite väärtustel (nagu eelneval joonisel)

Kui tavaline interaktsioonimudel on \(y = a + b_1x_1 + b_2x_2 + b_3x_1x_2\), siis mis juhtub, kui meie mudel on \(y = b_1x_1 + b_3x_1x_2\)? See tähendab, et me surume b2 väärtuse nulli, mis võib ära rikkuda mudeli teiste parameetrite posteeriorid! Kui teil on alust arvata, et b2-l puudub otsene mõju y väärtusele (kuid tal on mõju b1 väärtusele), siis võib muidugi ka sellist mudelit kasutada. Aga see on haruldane juhtum.