21 brms

brms on pakett, mis võimaldab kirjutada lihtsat süntaksit kasutades ka üsna keerulisi mudeleid ja need Stan-is fittida. Brms on loodud Paul Bürkneri poolt (https://github.com/paul-buerkner/brms), mis on oma kasutuslihtsuse tõttu jõudnud isegi ette Stani meeskonna arendatavast analoogsest paketist rstanarm (https://github.com/stan-dev/rstanarm/blob/master/README.md). Paul Bürkner oli mõned aastad tagasi psühholoogia doktorant, kes kirjutas brms-i algselt naljaviluks oma doktoriprojekti kõrvalt, mille tulemusel on ta praegu teatud ringkonnis tuntum kui Lady Gaga.

rstanarm, mide me siin ei käsitle, püüab pakkuda tavalisete sageduslikele meetoditele (ANOVA, lineaarne regressioon jne) bayesi analooge, mille mudeli spetsifikatsioon ja väljund erineks võimalikult vähe tavalisest baas-R-i töövoost. brms on keskendunud mitmetasemelistele mudelitele ja kasutab põhimõtteliselt lme4 (https://github.com/lme4/lme4/) mudelite keelt. Loomulikult saab brms-is fittida ka lineaarseid ja mitte-lineaareid ühetasemelisi mudeleid, nagu ka imputeerida andmeid ja teha palju muud (nagu näiteks pitsat valmistada).

library(tidyverse)
library(skimr)
library(brms)
library(loo)
library(broom)
library(bayesplot)
library(gridExtra)
library(mice)
library(pROC)

21.1 brms-i töövoog

brms-iga modelleerimisel on mõned asjad, mida tuleks teha sõltumata sellest, millist mudelit te parajasti fitite. Kõigepealt peaksite kontrollima, et mcmc ahelad on korralikult jooksnud (divergent transitions, rhat ja ahelate visuaalne inspekteerimine). Lisaks peaksite tegema posterioorse prediktiivse ploti ja vaatama, kui palju mudeli poolt genereeritud uued valimid meenutavad teie valimit. Samuti peaksite joonisel plottima residuaalid. Kui te inspekteerite fititud parameetrite väärtusi, siis tehke seda posteeriorite tasemel, k.a. koos veapiiridega. Kindlasti tuleks ka plottida mudeli ennustused koos usalduspiiridega.

Enne tõsist mudeldamist kiikame irise andmetabelisse

skim(iris)
#> Skim summary statistics
#>  n obs: 150 
#>  n variables: 5 
#> 
#> ── Variable type:factor ────────────────────────────────────────────────────────────────────────
#>  variable missing complete   n n_unique                       top_counts
#>   Species       0      150 150        3 set: 50, ver: 50, vir: 50, NA: 0
#>  ordered
#>    FALSE
#> 
#> ── Variable type:numeric ───────────────────────────────────────────────────────────────────────
#>      variable missing complete   n mean   sd  p0 p25  p50 p75 p100
#>  Petal.Length       0      150 150 3.76 1.77 1   1.6 4.35 5.1  6.9
#>   Petal.Width       0      150 150 1.2  0.76 0.1 0.3 1.3  1.8  2.5
#>  Sepal.Length       0      150 150 5.84 0.83 4.3 5.1 5.8  6.4  7.9
#>   Sepal.Width       0      150 150 3.06 0.44 2   2.8 3    3.3  4.4

ggplot(iris, aes(Petal.Length, Sepal.Length)) + 
  geom_point(aes(color = Species)) +
  geom_smooth(method = "loess", color = "black") +
  geom_smooth(method = "lm")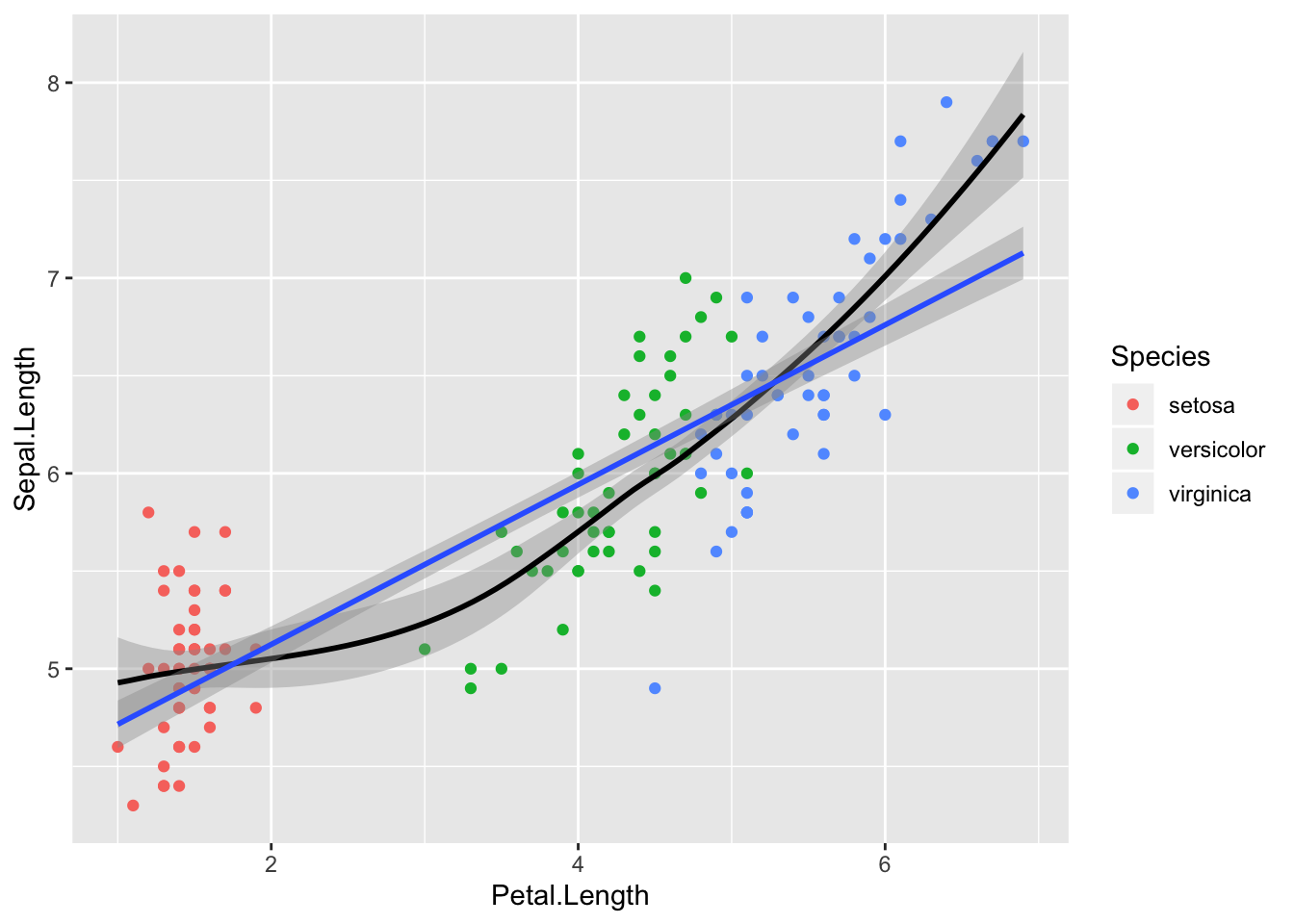

Loess fit viitab, et 3 liiki ühe sirgega mudeldada pole võib-olla optimaalne lahendus.

ggplot(iris, aes(Petal.Length, Sepal.Length, color = Species)) + 
  geom_point() +
  geom_smooth(method = "loess", aes(group = Species), color = "black") +
  geom_smooth(method = "lm")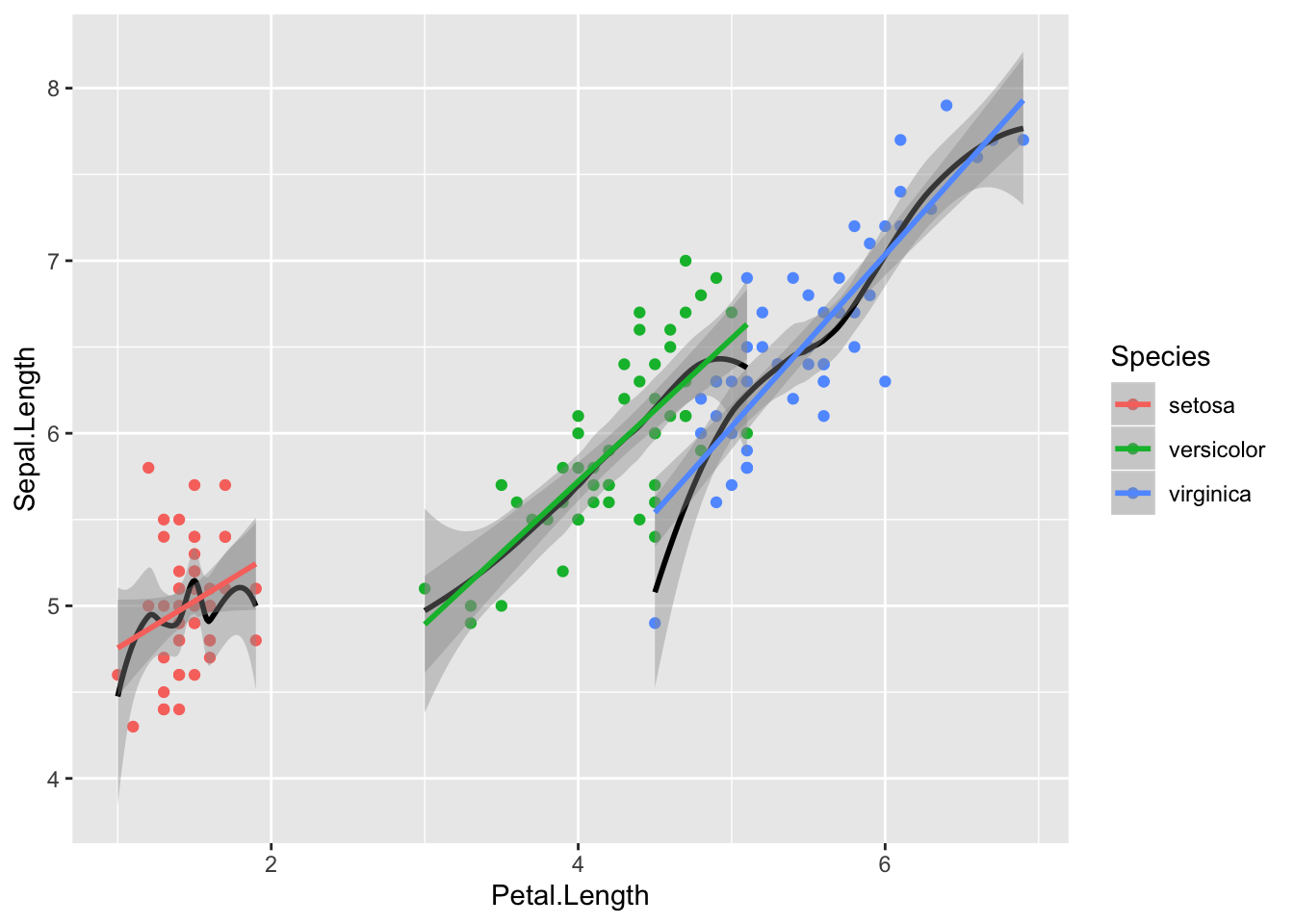

Nüüd on loess ja lm heas kooskõlas - seos y~x vahel oleks nagu enam-vähem lineaarne. Siit tuleb ka välja, et kolme mudeli tõusud on sarnased, interceptid erinevad.

21.1.1 Kiire töövoog

Minimaalses töövoos anname ette võimalikult vähe parameetreid ja töötame mudeliga nii vähe kui võimalik. See on mõeldud ülevaatena Bayesi mudeli fittimise põhilistest etappidest

Mudeli fittimine:

m_kiire <- brm(Sepal.Length ~ Petal.Length, data = iris)
write_rds(m_kiire, path = "data/m_kiire.fit")

Priorid on brms-i poolt ette antud ja loomulikult ei sisalda mingit teaduslikku informatsiooni. Nad on siiski “nõrgalt informatiivsed” selles mõttes, et kasutavad parametriseeringuid, mis enamasti võimaldavad mcmc ahelatel normaalselt joosta. Järgmises ptk-s õpime ise prioreid määrama.

Posteeriorid ja mcmc ahelate konvergents

plot(m_kiire)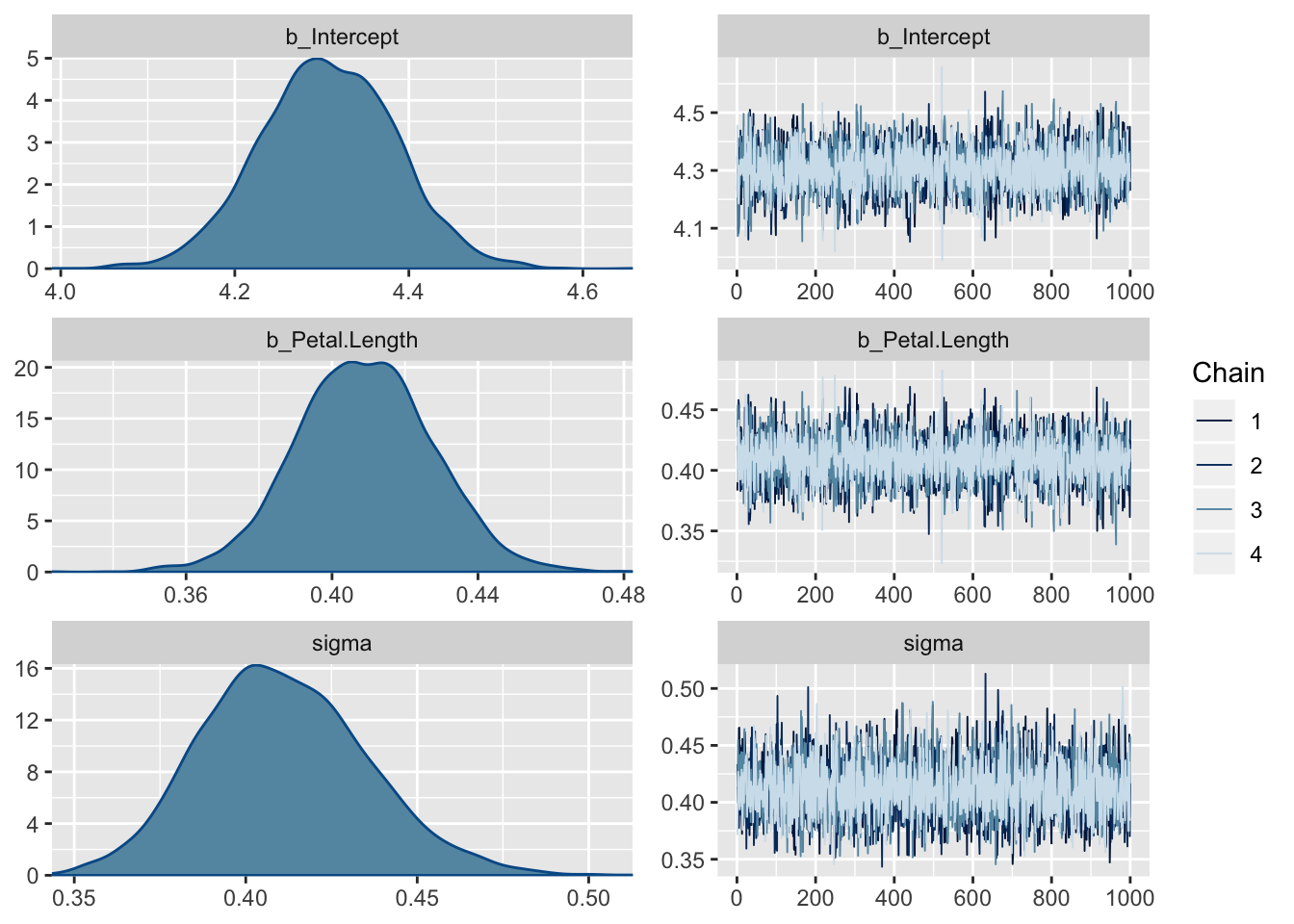

Fiti kokkuvõte - koefitsiendid ja nende fittimise edukust hindavad statistikud (Eff.Sample, Rhat)

tidy(m_kiire)
#>             term estimate std.error   lower   upper
#> 1    b_Intercept    4.307    0.0780   4.179   4.434
#> 2 b_Petal.Length    0.409    0.0187   0.379   0.439
#> 3          sigma    0.411    0.0243   0.373   0.453
#> 4           lp__  -85.338    1.2173 -87.757 -84.015

Eff.Sample näitab efektiivset valimi suurust, mida ahelad on kasutanud. See on suht keeruline mõiste, aga piisab, kui aru saada, et see näitaja ei tohiks olla madalam kui paarkümmend.

Rhat on statistik, mis vaatab ahelate konvergentsi. Kui Rhat > 1.1, siis on kuri karjas. Rhat 1.0 ei tähenda paraku, et võiks rahulikult hingata – tegu on statistikuga, mida saab hästi tõlgendada häda kuulutajana, aga liiga sageli mitte vastupidi.

Ennustav plot ehk marginal plot – mudeli fit 95% CI-ga.

plot(marginal_effects(m_kiire), points = TRUE)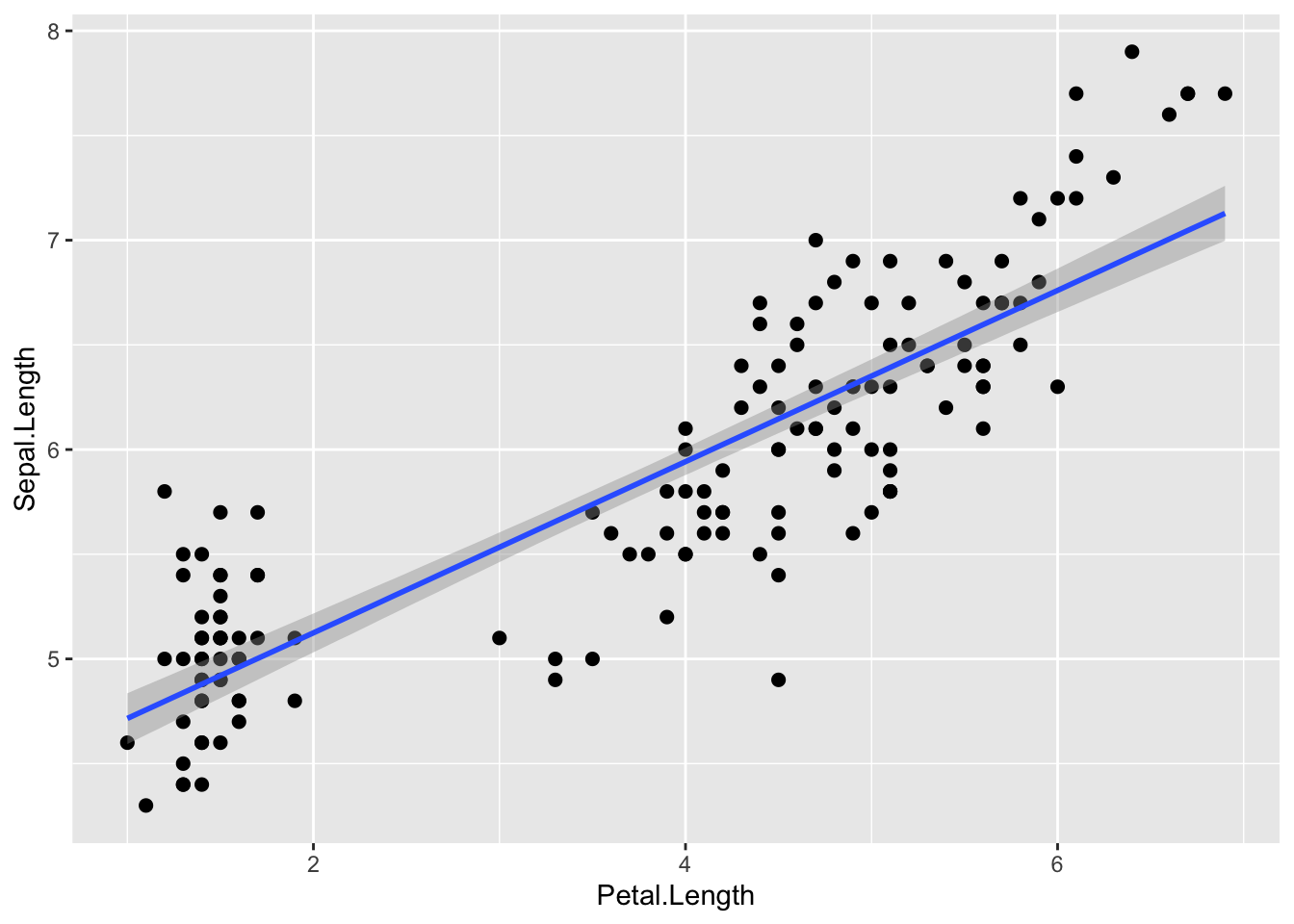

21.1.2 Põhjalikum töövoog

Põhiline erinevus eelmisega on suurem tähelepanu prioritele, mudeli fittimise diagnostikale ning tööle fititud mudeliga.

21.1.3 Spetsifitseerime mudeli, vaatame ja muudame vaikeprioreid

brms-i default priorid on konstrueeritud olema üsna väheinformatiivsed ja need tuleks enamasti informatiivsematega asendada. Igasse priorisse tuleks panna nii palju informatsiooni, kui teil on vastava parameetri kohta. Kui te mõne parameetri kohta ei oska öelda, milllised oleks selle mõistlikud oodatavad väärtused, siis saab piirduda brms-i antud vaikeväärtustega. Samas, kui keerulisemad mudelid ei taha hästi joosta (mida tuleb ikka ette), siis aitab sageli priorite kitsamaks muutmine.

get_prior(Sepal.Length ~ Petal.Length + (1 | Species), 
          data = iris)
#>                 prior     class         coef   group resp dpar nlpar bound
#> 1                             b                                           
#> 2                             b Petal.Length                              
#> 3 student_t(3, 6, 10) Intercept                                           
#> 4 student_t(3, 0, 10)        sd                                           
#> 5                            sd              Species                      
#> 6                            sd    Intercept Species                      
#> 7 student_t(3, 0, 10)     sigma

Me fitime pedagoogilistel kaalutlustel shrinkage mudeli, mis tõmbab 3 liigi lõikepunkte natuke keskmise lõikepunkti suunas. On vaieldav, kas see on irise andmestiku juures mõistlik strateegia, aga me teeme seda siin ikkagi.

Mitmetasemeline shrinkage mudel on abinõu ülefittimise vastu. Mudelite võrdlemisel otsitakse kompromissi - ehk mudeli, mille ennustused oleks andmepunktidele võimalikult lähedal ilma,et see mudel oleks liiga keeruliseks aetud (keerulisus on proportsionaalne mudeli parameetrite arvuga).

Prioreid muudame nii:

prior <- c(prior(normal(6, 3), class = "Intercept"),
           prior(normal(0, 1), class = "b"),
           prior(student_t(6, 0, 2), class = "sigma"))

Me valime siin nn väheinformariivsed priorid, nii et regressiooni tulemus on suht hästi võrreldav lme4 sagedusliku mudeliga. “b” koefitsiendi priorile (aga mitte “sigma” ega “Intercept”-le) võib anda ka ülemise ja/või alumise piiri prior(normal(0, 1), class = "b", lb = -1, ub = 10) ütleb, et “b” prior on nullist erinev ainult -1 ja 10 vahel. “sigma” priorid on automaatselt lb = 0-ga, sest varieeruvus ei tohi olla negatiivne.

Alati tasub prioreid pildil vaadata, et veenduda nende mõistlikuses.

x <- seq(0, 10, length.out = 100)
y <- dstudent_t(x, df = 6, mu = 0, sigma = 2, log = FALSE)
plot(y ~ x)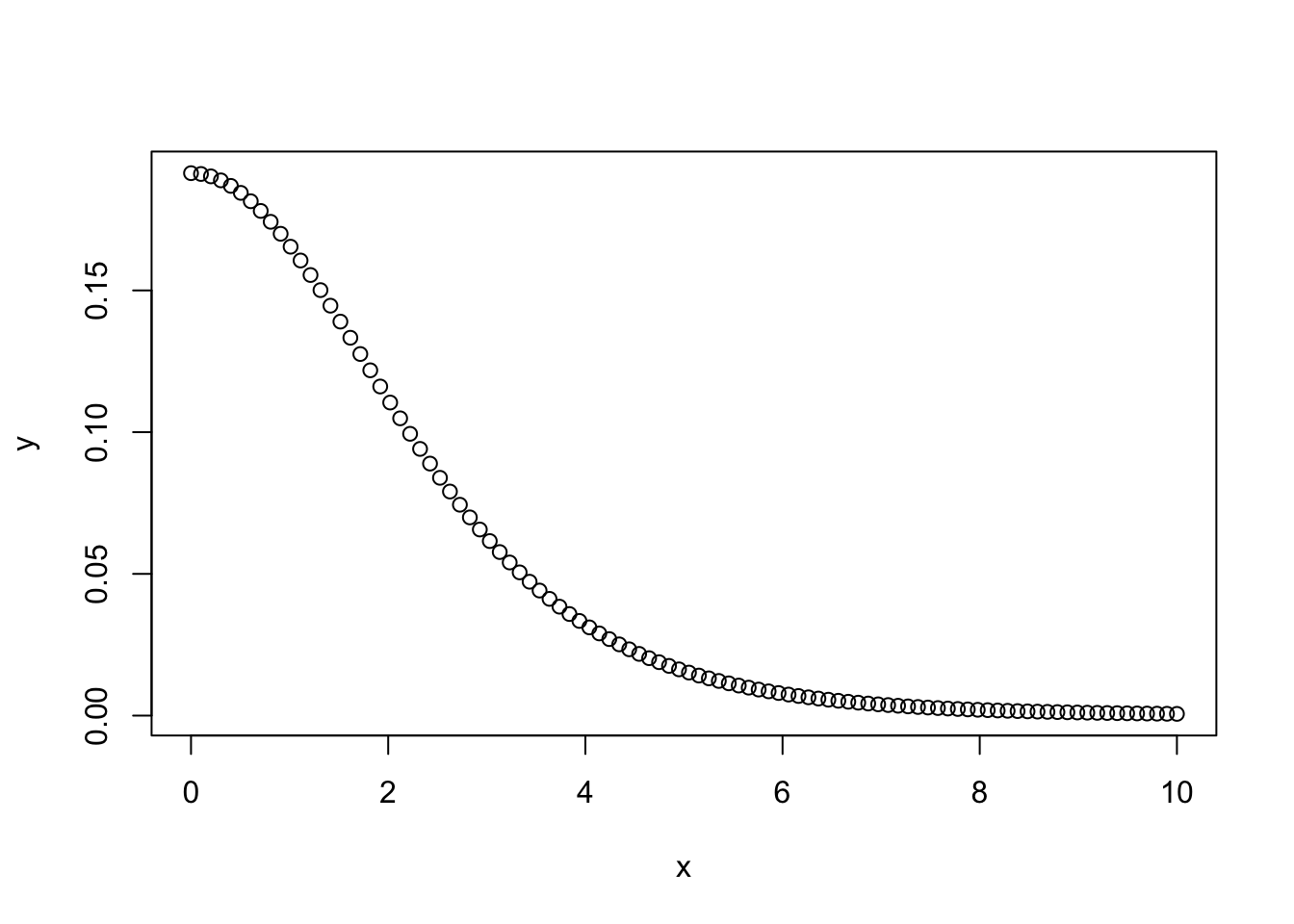

Sigma prior, mida brms kasutab, on vaikimisi pool sümmeetrilisest jaotusest, mis lõigatakse nulli kohalt pooleks nii, et seal puuduvad < 0 väärtused (seega ei saa varieeruvuse posteerior minna alla nulli).

Me võime ka prioreid ilma likelihoodideta (tõepärafunktsioonideta) läbi mudeli lasta, misjärel tõmbame fititud mudelist priorite valimid (neid võiks kutsuda ka “priorite posteerioriteks”) ja plotime kõik priorid koos. Seda pilti saab siis võrrelda koos andmetega fititud mudeli posteerioritega. Selle võimaluse kasutamine on tõusuteel, sest keerulisemate mudelite puhul võib priorite ükshaaval plottimine osutuda eksitavaks.

Tekitame priorite valimid, et näha oma priorite mõistlikust (brm() argument on sample_prior = TRUE). Ühtlasi fitime ka oma mudeli koos andmete ja prioritega.

m1 <- brm(Sepal.Length ~ Petal.Length + (1 | Species), 
          data = iris, 
          prior = prior, 
          family = gaussian,
          warmup = 1000,
          iter = 2000,
          chains = 3,
          cores = 3,
          sample_prior = TRUE)
write_rds(m1, path = "data/m1.fit")

Me fittisime mudeli m1 kaks korda: nii andmetega (selle juurde jõuame varsti), kui ka ilma andmeteta. Kui panna sisse sample_prior = "only", siis jookseb mudel ilma andmeteta, ja selle võrra kiiremini. Vaikeväärtus on sample_prior = "no", mis tähendab, et fititakse ainult üks mudel - koos andmetega. Ilma andmeteta (likelihoodita) fitist saame tõmmata priorite mcmc valimid, mille ka järgmiseks plotime.

prior_samples(m1) %>% 
  gather() %>% 
  ggplot() + 
  geom_density(aes(value)) + 
  facet_wrap(~ key, scales = "free_x")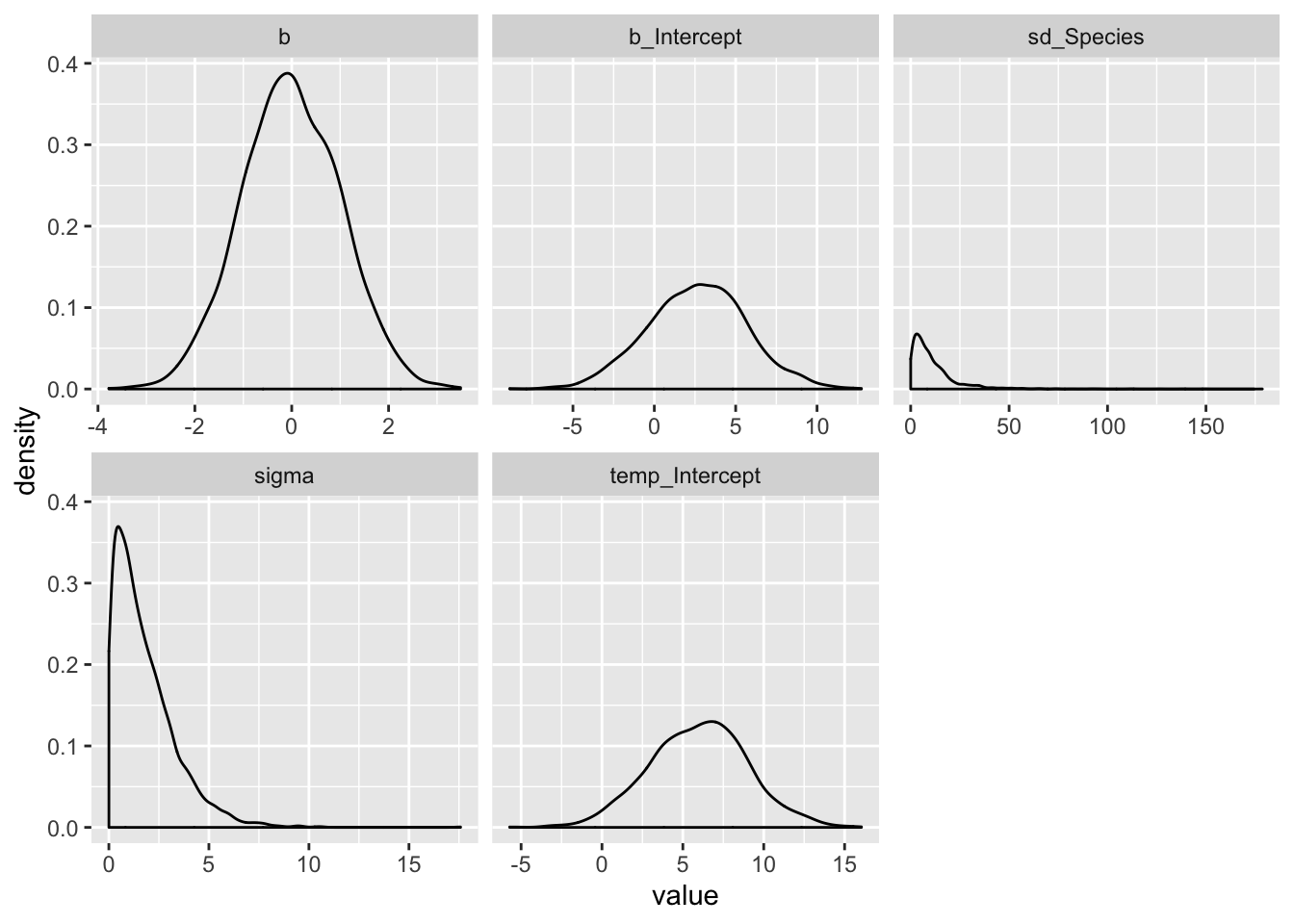

Kui kasutame sample_prior = "only" varianti, siis on esimene koodirida erinev: samples1 = as.data.frame(m1$fit).

brms-i Intercepti priorite spetsifitseerimisel tasub teada, et brms oma sisemuses tsentreerib kõik prediktorid nullile (x - mean(x)), ja teie poolt ette antud prior peaks vastama neile tsentreeritud prediktoritele, kus kõikide prediktorite keskväärtus on null. Põhjus on, et tsentreeritud parametriseeringuga mudelid jooksevad sageli paremini. Alternatiiv on kasutada mudeli tavapärase süntaksi y ~ 1 + x (või ekvivalentselt y ~ x) asemel süntaksit y ~ 0 + intercept + x. Sellisel juhul saab anda priorid tsentreerimata predikroritele. Lisaks on brms selle süntaksi puhul nõus “b”-le antud prioreid vaikimisi ka intercepti fittimisel kasutama.

21.1.4 `brm()` funktsiooni argumendid:

family - tõepärafunktsiooni tüüp (modelleerib y muutuja jaotust e likelihoodi)
warmup - mitu sammu mcmc ahel astub, enne kui ahelat salvestama hakatakse. tavaliselt on 500-1000 sammu piisav, et tagada ahelate konvergents. Kui ei ole, tõstke 2000 sammuni.
iter - ahelate sammude arv, mida salvestatakse peale warmup perioodi. Enamasti on 2000 piisav. Kui olete nõus piirduma posteeriori keskväärtuse arvutamisega ja ei soovi täpseid usaldusintervalle, siis võib piisata ka 200 sammust.
chains - mitu sõltumatut mcmc ahelat jooksutada. 3 on hea selleks, et näha kas ahelad konvergeeruvad. Kui mitte, tuleks lisada informatiivsemaid prioreid ja/või warmupi pikkust.
cores - mitu teie arvuti tuuma ahelaid jooksutama panna.
adapt_delta - mida suurem number (max = 1), seda stabiilsemalt, ja aeglasemalt, ahelad jooksevad.
thin - kui ahel on autokorreleeritud, st ahela eelmine samm suudab ennustada järgevaid (see on paha), siis saab salvestada näit ahela iga 5. sammu (thin = 5). Aga siis tuleks ka sammude arvu 5 korda tõsta. Vaikeväärtus on thin = 1. Autokorrelatsiooni graafilist määramist näitame allpool

Järgmine funktsioon trükib välja Stani koodi, mis spetsifitseerib mudeli, mida tegelikult Stanis fittima hakatakse. See on väga kasulik, aga ainult siis kui tahate õppida otse Stanis mudeleid kirjutama:

make_stancode(Sepal.Length ~ Petal.Length, data = iris, prior = prior)

21.1.5 Fitime mudeleid ja võrdleme fitte.

Eelmises mudelis (m1) ennustame muutuja Sepal.Length väärtusi Petal.Length väärtuste põhjal shrinkage mudelis, kus iga irise liik on oma grupis.

Teine mudel, mis sisaldab veel üht ennustavat muutujat (Sepal.Width):

m2 <- brm(Sepal.Length ~ Petal.Length + Sepal.Width + (1 | Species), 
          data = iris, 
          prior = prior)
write_rds(m2, path = "data/m2.fit")

Kolmandaks ühetasemeline mudel, mis vaatab kolme irise liiki eraldi:

m3 <- brm(Sepal.Length ~ Sepal.Width + Petal.Length * Species, 
          data = iris, 
          prior = prior)
write_rds(m3, path = "data/m3.fit")

Ja lõpuks mudel, mis paneb kõik liigid ühte patta:

m4 <- brm(Sepal.Length ~ Petal.Length + Sepal.Width, 
          data = iris, 
          prior = prior)
write_rds(m4, path = "data/m4.fit")

Siin me võrdleme neid nelja mudelit. Väikseim looic (leave-one-out information criterion) võidab. See on suhteline võrdlus – looic abs väärtus ei mängi mingit rolli.

loo(m1, m2, m3, m4)
#> Warning: Passing multiple brmsfit objects to 'loo' and related methods is
#> deprecated. Please see ?loo.brmsfit for the recommended workflow.
#> Output of model 'm1':
#> 
#> Computed from 3000 by 150 log-likelihood matrix
#> 
#>          Estimate   SE
#> elpd_loo    -53.2  8.3
#> p_loo         4.8  0.7
#> looic       106.4 16.6
#> ------
#> Monte Carlo SE of elpd_loo is 0.1.
#> 
#> All Pareto k estimates are good (k < 0.5).
#> See help('pareto-k-diagnostic') for details.
#> 
#> Output of model 'm2':
#> 
#> Computed from 3000 by 150 log-likelihood matrix
#> 
#>          Estimate   SE
#> elpd_loo    -40.8  8.1
#> p_loo         5.6  0.7
#> looic        81.6 16.1
#> ------
#> Monte Carlo SE of elpd_loo is 0.1.
#> 
#> All Pareto k estimates are good (k < 0.5).
#> See help('pareto-k-diagnostic') for details.
#> 
#> Output of model 'm3':
#> 
#> Computed from 3000 by 150 log-likelihood matrix
#> 
#>          Estimate   SE
#> elpd_loo    -40.0  7.9
#> p_loo         7.1  0.9
#> looic        80.0 15.8
#> ------
#> Monte Carlo SE of elpd_loo is 0.1.
#> 
#> All Pareto k estimates are good (k < 0.5).
#> See help('pareto-k-diagnostic') for details.
#> 
#> Output of model 'm4':
#> 
#> Computed from 3000 by 150 log-likelihood matrix
#> 
#>          Estimate   SE
#> elpd_loo    -50.3  8.2
#> p_loo         3.5  0.5
#> looic       100.5 16.4
#> ------
#> Monte Carlo SE of elpd_loo is 0.0.
#> 
#> All Pareto k estimates are good (k < 0.5).
#> See help('pareto-k-diagnostic') for details.
#> 
#> Model comparisons:
#>    elpd_diff se_diff
#> m3   0.0       0.0  
#> m2  -0.8       1.7  
#> m4 -10.3       5.0  
#> m1 -13.2       5.3

Siin on m1 ja m2/m3 mudeli erinevus 25 ühikut ja selle erinevuse standardviga on 10 ühikut. 2 SE-d annab umbkaudu 95% usaldusintervalli, ja see ei kata antud juhul nulli. Seega järeldame, et m2 ja m3, mis kasutavad ennustamiseks lisamuutujat, on selgelt eelistatud. Samas ei saa me õelda, et hierarhiline mudel m2 oleks parem või halvem kui interaktsioonimudel m3. Ka puudub oluline erinevus m1 ja m4 fiti vahel. Tundub, et selle ennustusjõu, mille me võidame lisaparameetrit mudeldades, kaotame omakorda liike ühte patta pannes (neid mitte osaliselt iseseisvana modelleerides).

Alternatiivina kasutame brms::waic kriteeriumit mudelite võrdlemiseks. See töötab kiiremini kui LOO ja tõlgendus on sarnane - väikseim waic võidab ja absolutväärtusi ei saa ükshaaval tõlgendada.

waic(m1, m2, m3, m4)
#> Warning: Passing multiple brmsfit objects to 'loo' and related methods is
#> deprecated. Please see ?loo.brmsfit for the recommended workflow.
#> Output of model 'm1':
#> 
#> Computed from 3000 by 150 log-likelihood matrix
#> 
#>           Estimate   SE
#> elpd_waic    -53.2  8.3
#> p_waic         4.8  0.7
#> waic         106.4 16.6
#> Warning: 1 (0.7%) p_waic estimates greater than 0.4. We recommend trying
#> loo instead.
#> 
#> Output of model 'm2':
#> 
#> Computed from 3000 by 150 log-likelihood matrix
#> 
#>           Estimate   SE
#> elpd_waic    -40.8  8.0
#> p_waic         5.6  0.7
#> waic          81.6 16.1
#> 
#> Output of model 'm3':
#> 
#> Computed from 3000 by 150 log-likelihood matrix
#> 
#>           Estimate   SE
#> elpd_waic    -40.0  7.9
#> p_waic         7.0  0.9
#> waic          80.0 15.8
#> Warning: 1 (0.7%) p_waic estimates greater than 0.4. We recommend trying
#> loo instead.
#> 
#> Output of model 'm4':
#> 
#> Computed from 3000 by 150 log-likelihood matrix
#> 
#>           Estimate   SE
#> elpd_waic    -50.3  8.2
#> p_waic         3.5  0.5
#> waic         100.5 16.4
#> 
#> Model comparisons:
#>    elpd_diff se_diff
#> m3   0.0       0.0  
#> m2  -0.8       1.7  
#> m4 -10.3       5.0  
#> m1 -13.2       5.3

Nagu näha, annavad LOO ja waic sageli väga sarnaseid tulemusi.

Me ei süvene LOOIC ega waic-i statistilisse mõttesse, sest bayesi mudelite võrdlemine on kiiresti arenev ala, kus ühte parimat lahendust pole veel leitud.

21.1.6 Vaatame mudelite kokkuvõtet

Lihtne tabel mudeli m2 fititud koefitsientidest koos 95% usalduspiiridega

tidy(m2)
#>                              term estimate std.error   lower   upper
#> 1                     b_Intercept    1.710    1.0270   0.095   3.345
#> 2                  b_Petal.Length    0.759    0.0645   0.651   0.866
#> 3                   b_Sepal.Width    0.440    0.0839   0.303   0.576
#> 4           sd_Species__Intercept    1.725    1.5315   0.433   5.024
#> 5                           sigma    0.313    0.0186   0.284   0.345
#> 6     r_Species[setosa,Intercept]    0.676    0.9925  -0.901   2.250
#> 7 r_Species[versicolor,Intercept]   -0.226    0.9842  -1.853   1.253
#> 8  r_Species[virginica,Intercept]   -0.642    0.9907  -2.277   0.809
#> 9                            lp__  -50.433    2.3680 -54.788 -47.169

r_ prefiks tähendab, et antud koefitsient kuulub mudeli esimesele (madalamale) tasemele (Liigi tase) r - random - tähendab, et iga grupi (liigi) sees arvutatakse oma fit. b_ tähendab mudeli 2. taset (keskmistatud üle kõikide gruppide). 2. tasmel on meil intercept, b1 ja b2 tõusud ning standardhälve y muutuja ennustatud andempunktide tasemel. 1. tasemel on meil 3 liigi interceptide erinevus üldisest b_Intercepti väärtusest. Seega, selleks, et saada setosa liigi intercepti, peame tegema tehte 1.616 + 0.765.

tidy funktsiooni tööd saab kontrollida järgmiste parameetrite abil:

tidy(x, parameters = NA, par_type = c("all",
  "non-varying", "varying", "hierarchical"), robust = FALSE,
  intervals = TRUE, prob = 0.9, ...)

par_type = “hierarchical” kuvab grupi taseme parameetrite sd-d ja korrelatsioonid. “varying” kuvab grupi taseme interceptid ja tõusud (siis kui neid mudeldadakse). “non-varying” kuvab kõrgema taseme (grupi-ülesed) parameetrid. robust = TRUE annab estimate posteeriori mediaanina (vaikeväärtus FALSE annab selle aritmeetilise keskmisena posteeriorist).

Nüüd põhjalikum mudeli kokkuvõte:

m2
#> Warning: There were 17 divergent transitions after warmup. Increasing adapt_delta above 0.95 may help.
#> See http://mc-stan.org/misc/warnings.html#divergent-transitions-after-warmup
#>  Family: gaussian 
#>   Links: mu = identity; sigma = identity 
#> Formula: Sepal.Length ~ Petal.Length + Sepal.Width + (1 | Species) 
#>    Data: iris (Number of observations: 150) 
#> Samples: 3 chains, each with iter = 2000; warmup = 1000; thin = 1;
#>          total post-warmup samples = 3000
#> 
#> Group-Level Effects: 
#> ~Species (Number of levels: 3) 
#>               Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat
#> sd(Intercept)     1.72      1.53     0.36     5.98        515 1.00
#> 
#> Population-Level Effects: 
#>              Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat
#> Intercept        1.71      1.03    -0.36     4.08        594 1.01
#> Petal.Length     0.76      0.06     0.63     0.88       1478 1.00
#> Sepal.Width      0.44      0.08     0.27     0.60       1893 1.00
#> 
#> Family Specific Parameters: 
#>       Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat
#> sigma     0.31      0.02     0.28     0.35       1882 1.00
#> 
#> Samples were drawn using sampling(NUTS). For each parameter, Eff.Sample 
#> is a crude measure of effective sample size, and Rhat is the potential 
#> scale reduction factor on split chains (at convergence, Rhat = 1).

Siin on eraldi toodud grupi tasemel ja populatsiooni tasemel koefitsiendid ja gruppide vaheline sd (= 1.72). Pane tähele, et üldine varieeruvus sigma = 0.31 on palju väiksem kui gruppide vaheline varieeruvus sd(Intercept) = 1.72. Seega on grupid üksteisest tugevalt erinevad ja neid tuleks võib-olla tõesti eraldi modelleerida.

Divergentsed transitsioonid on halvad asjad - ahelad on läinud 17 korda metsa. Viisakas oleks adapt deltat tõsta või kitsamad priorid panna, aga 17 halba andmepunkti paarist tuhandest, mille mcmc ahelad meile tekitasid, pole ka mingi maailmalõpp. Nii et las praegu jääb nagu on. Need divergentsed transitsioonid on kerged tekkima just mitmetasemelistes mudelites.

21.1.7 Plotime posteeriorid ja ahelad

plot(m2)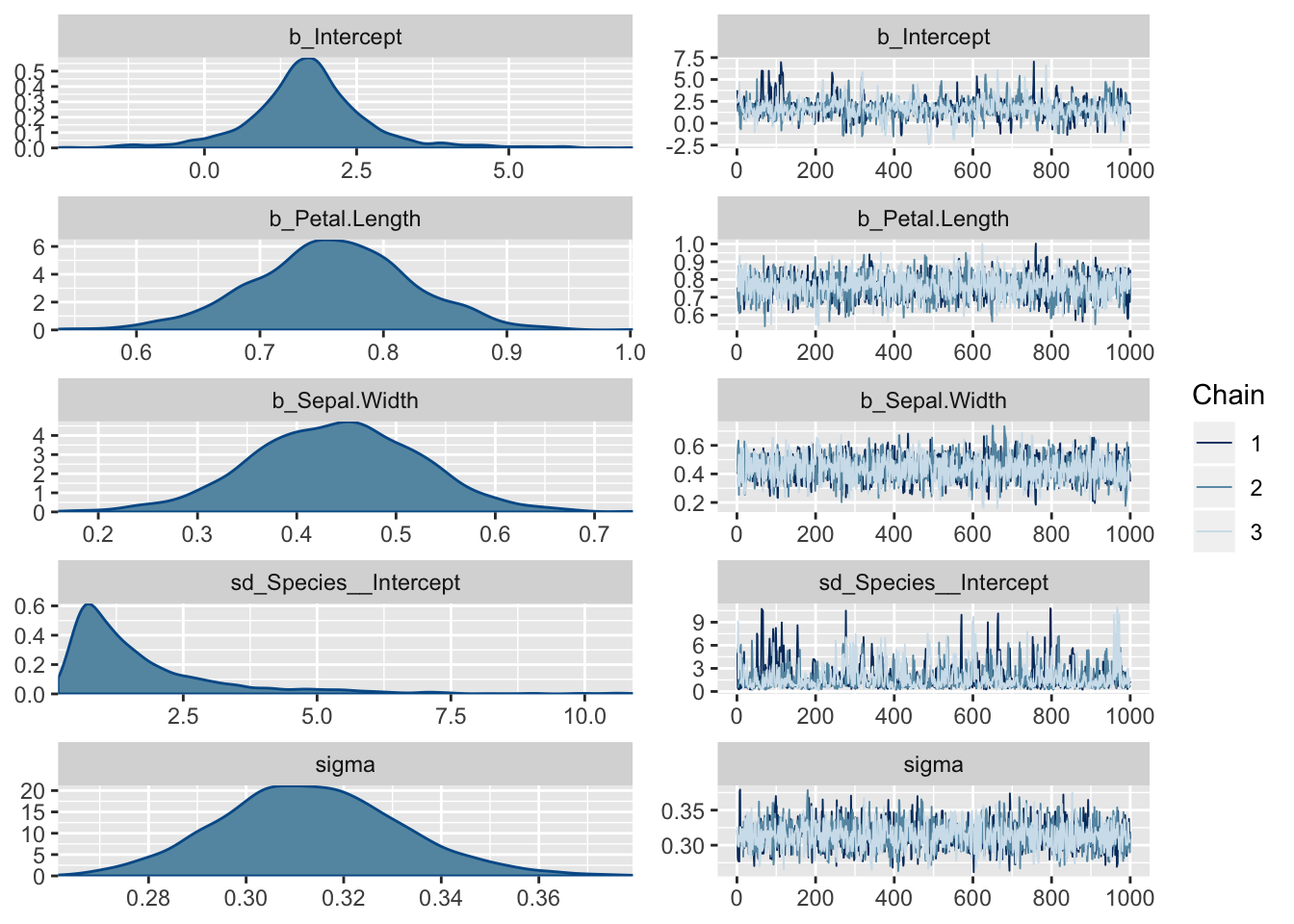

Siit on näha, et ahelad on ilusti konvergeerunud. Ühtlasi on pildil posterioorsed jaotused fititud koefitsientidele.

Regular expressioni abil saab plottida mudeli madalama taseme ahelaid & posteerioreid, mida plot() vaikimisi ei näita.

plot(m2, pars = "r_")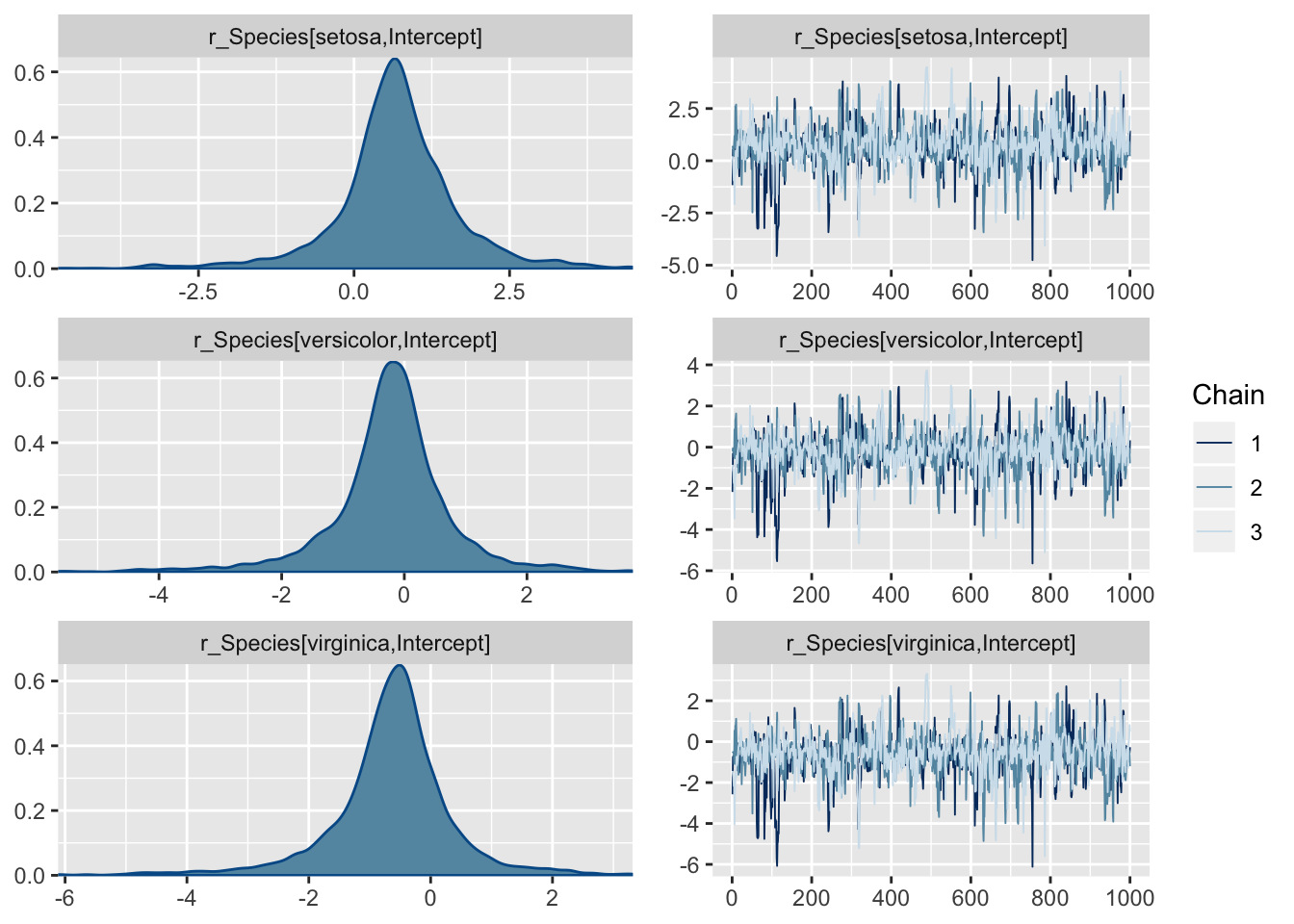

Vaatame korrelatsioone erinevate parameetrite posterioorsete valimite vahel. (Markovi ahelad jooksevad n-mõõtmelises ruumis, kus n on mudeli parameetrite arv, mille väärtusi hinnatakse.) Pairs(m3) teeb pildi ära, aga ilusama pildi saab GGally::ggpairs() abil.

pairs(m2, pars = "b_")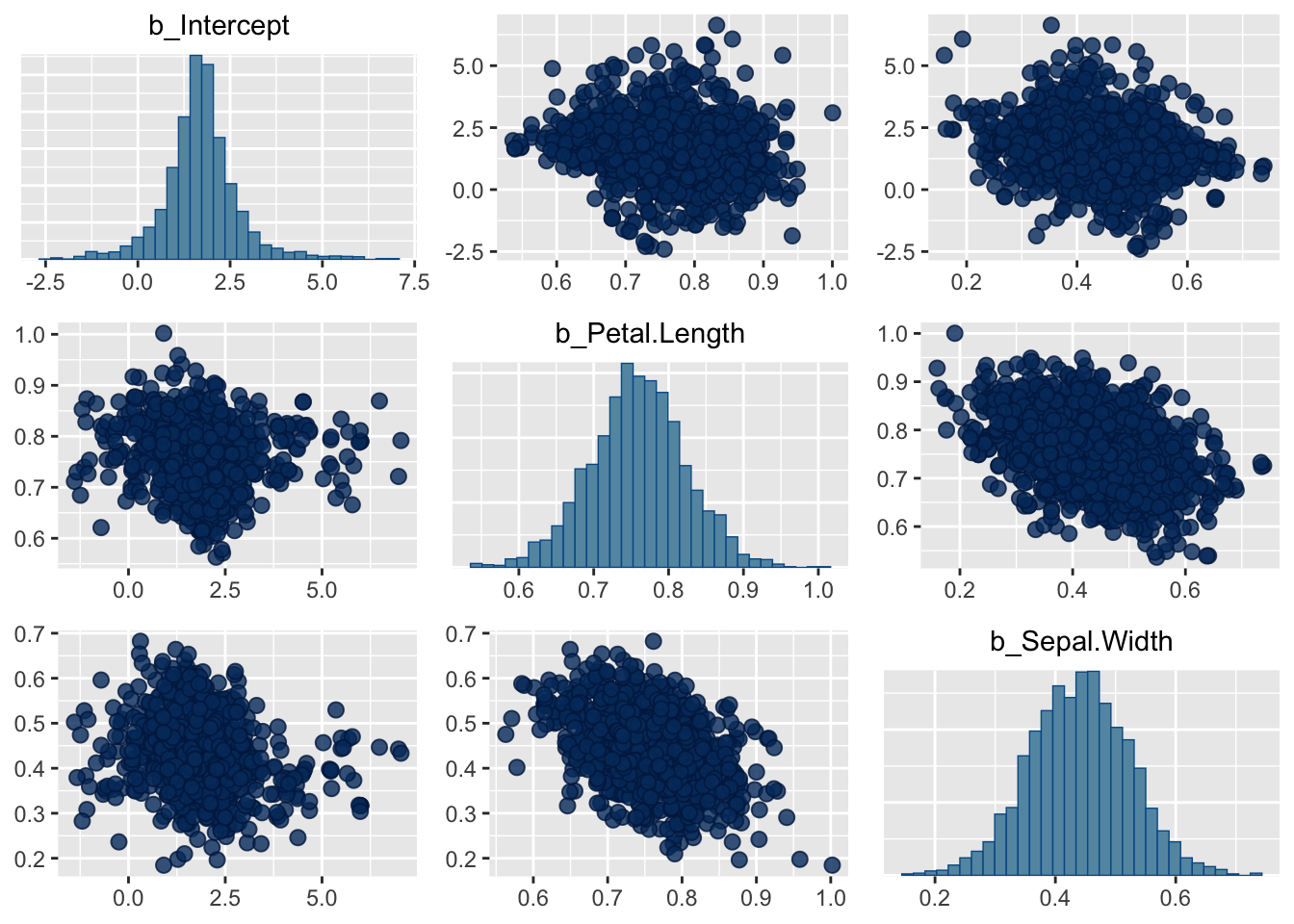

library(GGally)
posterior_samples(m2) %>%
  select(contains("b_")) %>%
  ggpairs()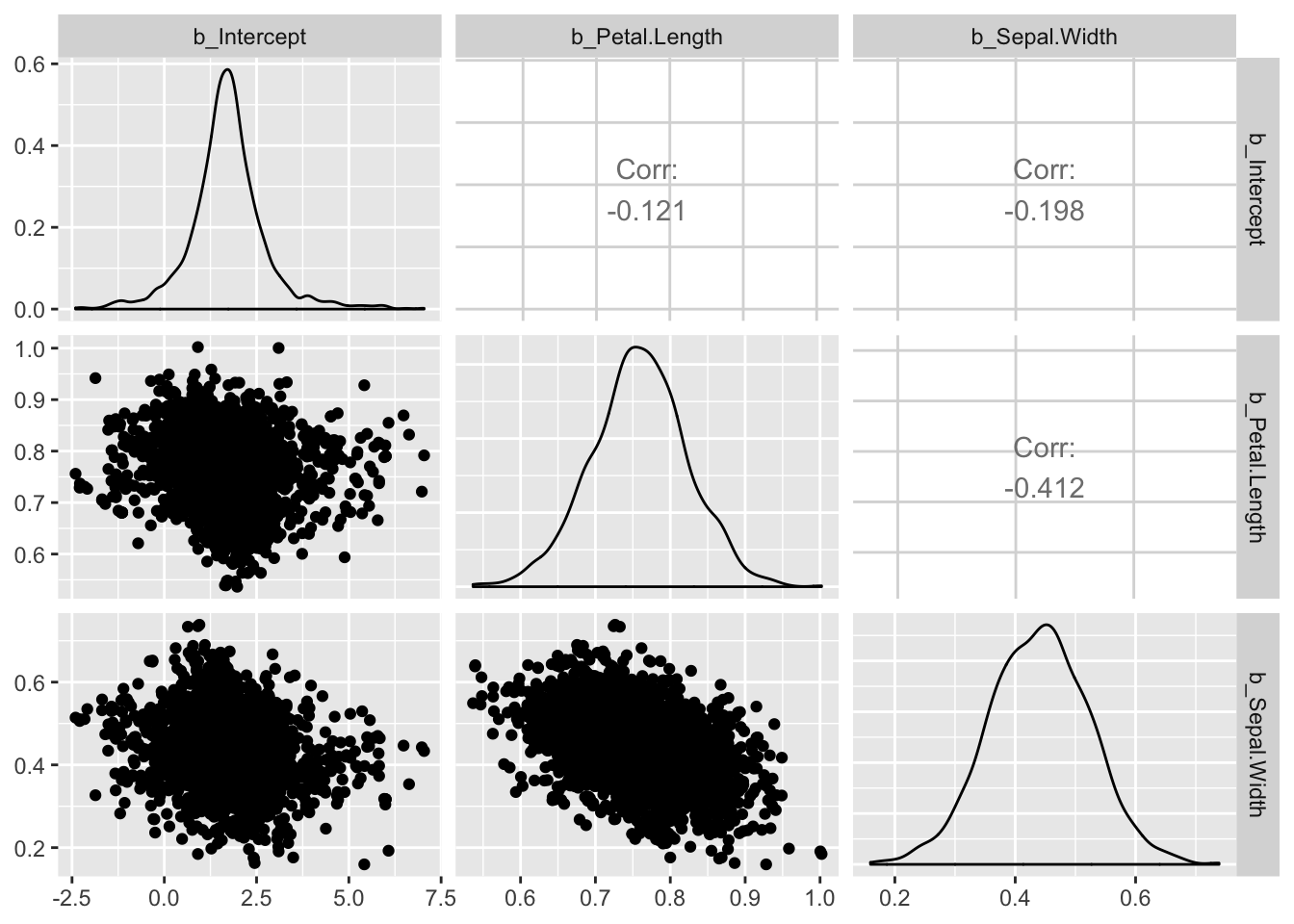

Siin on posteeriorite põhjal arvutatud 50% ja 95% CI ja see plotitud.

stanplot(m2, pars = "r_", type = "intervals")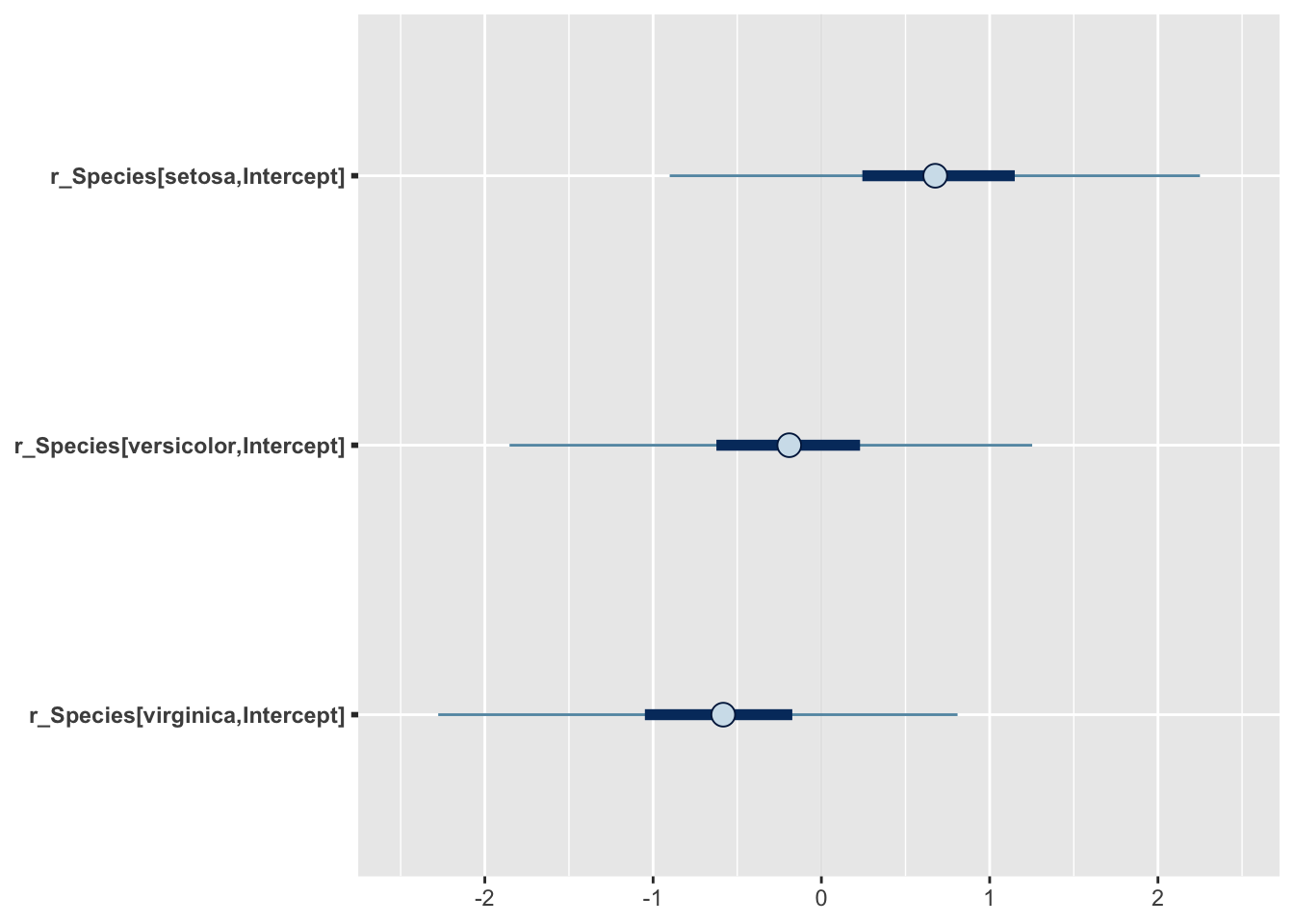

type = argument sisestamine võimaldab plottida erinevaid diagnostilisi näitajaid. Lubatud sisendid on “hist”, “dens”, “hist_by_chain”, “dens_overlay”, “violin”, “intervals”, “areas”, “acf”, “acf_bar”, “trace”, “trace_highlight”, “scatter”, “rhat”, “rhat_hist”, “neff”, “neff_hist” “nuts_acceptance”, “nuts_divergence”, “nuts_stepsize”, “nuts_treedepth” ja “nuts_energy”.

stanplot(m2, type = "neff")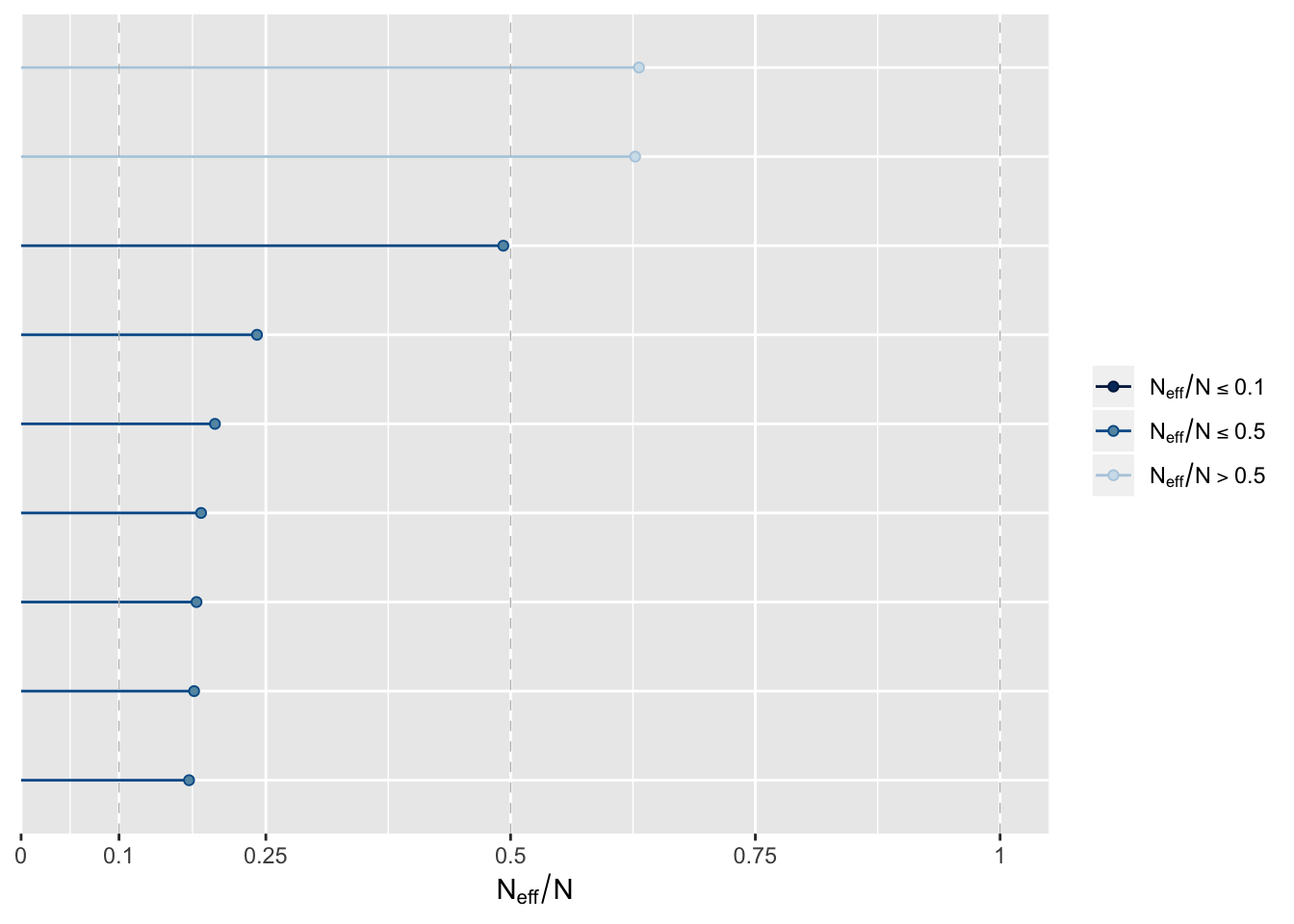

Neff on efektiivne valimi suurus ja senikaua kuni Neff/N suhe ei ole < 0.1, pole põhjust selle pärast muretseda.

21.1.8 Korjame ahelad andmeraami ja plotime fititud koefitsiendid CI-dega

model <- posterior_samples(m1)

mcmc_intervals() on bayesplot paketi funktsioon. me plotime 50% ja 95% CI-d.

pars <- colnames(model)
mcmc_intervals(model, regex_pars = "[^(lp__)]")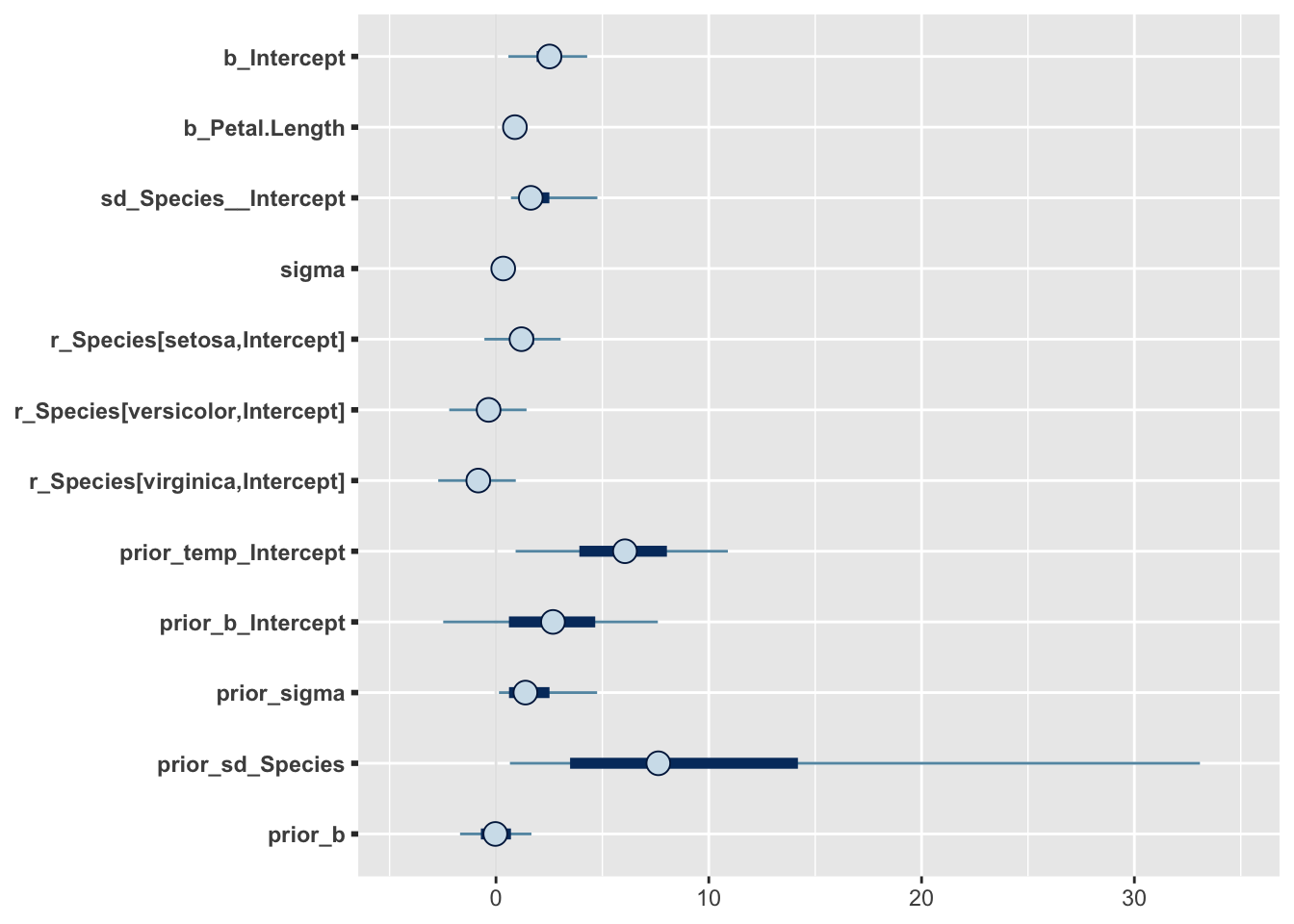

Näeme, et sigma hinnang on väga usaldusväärne, samas kui gruppide vahelise sd hinnang ei ole seda mitte (pane tähele posterioorse jaotuse ebasümmeetrilisust).

model2 <- posterior_samples(m2)
pars <- colnames(model2)
mcmc_intervals(model2, regex_pars = "[^(lp__)]")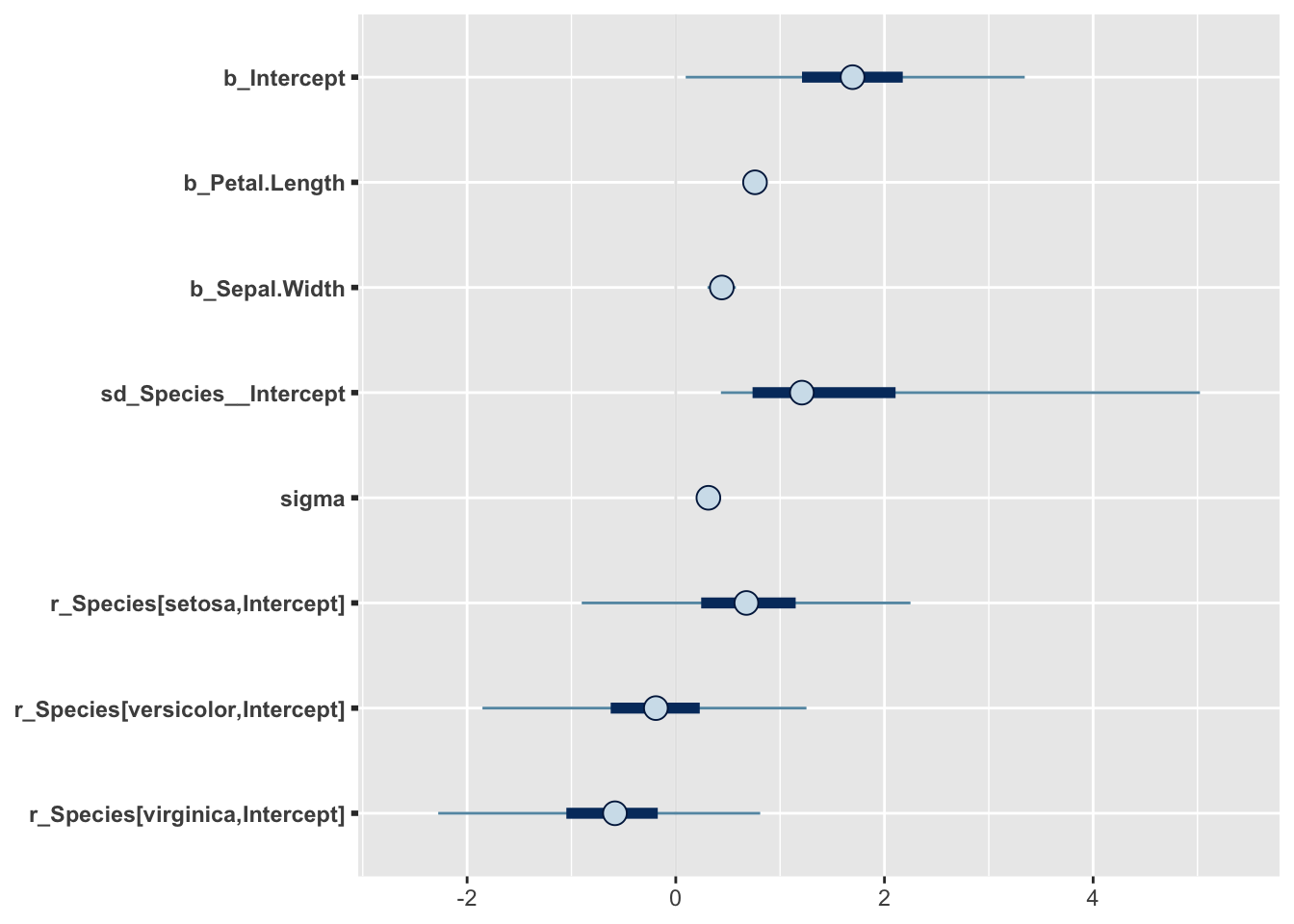

mcmc_areas(model2,  pars = c("b_Petal.Length", "b_Sepal.Width"))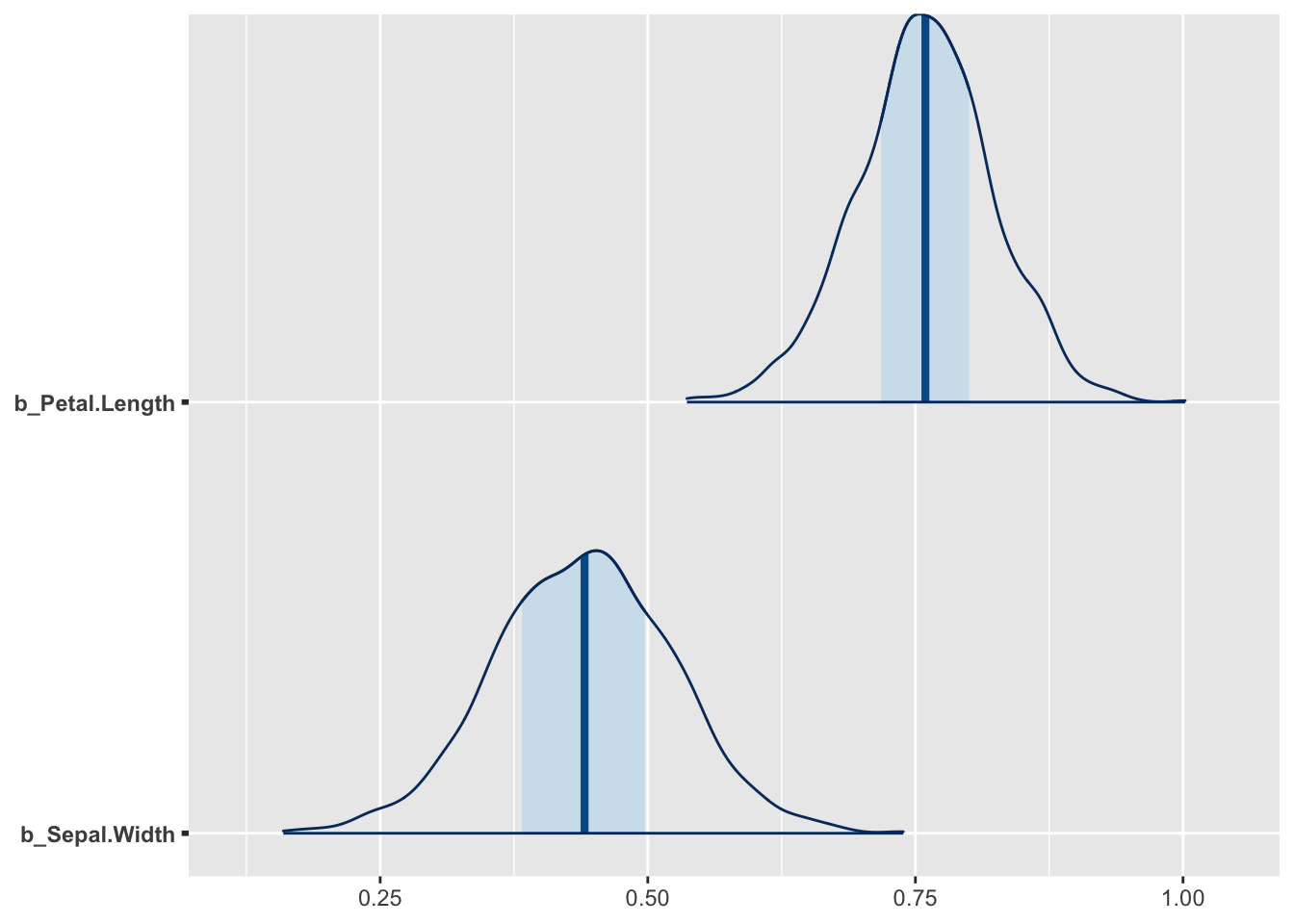

21.1.9 Bayesi versioon R-ruudust

Kui suurt osa koguvarieeruvusest suudavad mudeli prediktorid seletada?

bayes_R2(m2)
#>    Estimate Est.Error Q2.5 Q97.5
#> R2     0.86   0.00831 0.84 0.873

bayes_R2(m1)
#>    Estimate Est.Error  Q2.5 Q97.5
#> R2    0.833    0.0109 0.807  0.85

https://github.com/jgabry/bayes_R2/blob/master/bayes_R2.pdf Annab põhjenduse sellele statistikule (mille arvutamine erineb tavalisest vähimruutudega arvutatud mudeli $R^2$-st).

21.1.10 Plotime mudeli poolt ennustatud valimeid – posterior predictive check

Kui mudel suudab genereerida simuleeritud valimeid, mis ei erine väga palju empiirilisest valimist, mille põhjal see mudel fititi, siis võib-olla ei ole see täiesti ebaõnnestunud mudeldamine. See on loogika posterioorse ennustava ploti taga.

Vaatame siin simultaanselt kõigi kolme eelnevalt fititud mudeli simuleeritud valimeid (y_rep) võrdluses algsete andmetega (y):

purrr::map(list(m1, m2, m3), pp_check, nsamples = 10) %>% 
  grid.arrange(grobs = ., nrow = 3)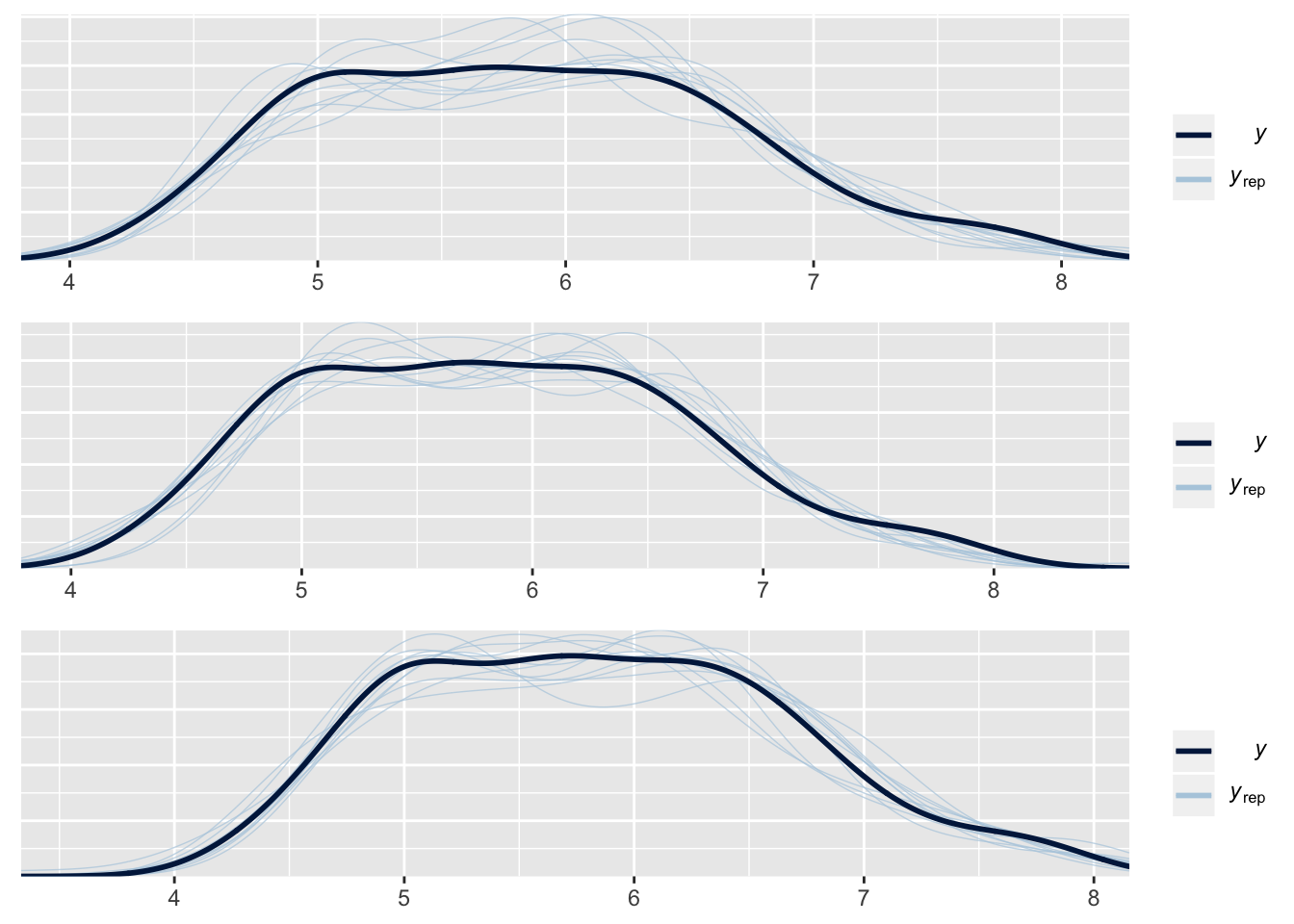

y - tihedusplot empiirilistest andmetest
y_rep – plotid mudeli poolt ennustatud iseseisvatest valimitest (igaüks sama suur kui empiiriline valim y) Jooniselt on näha, et m3 ennustused on võrreldes m1 ja m2-ga kõige kaugemal tegelikust valimist.

21.1.11 Plotime mudeli ennustusi - marginal effects plots

Teeme ennustused. Kõigepealt ennustame ühe keskmise mudeliga, mis ei arvesta mitmetasemelise mudeli madalamte tasemete koefitsientidega.

plot(marginal_effects(m2, effects = "Petal.Length", method = "predict", probs = c(0.1, 0.9)), points = TRUE)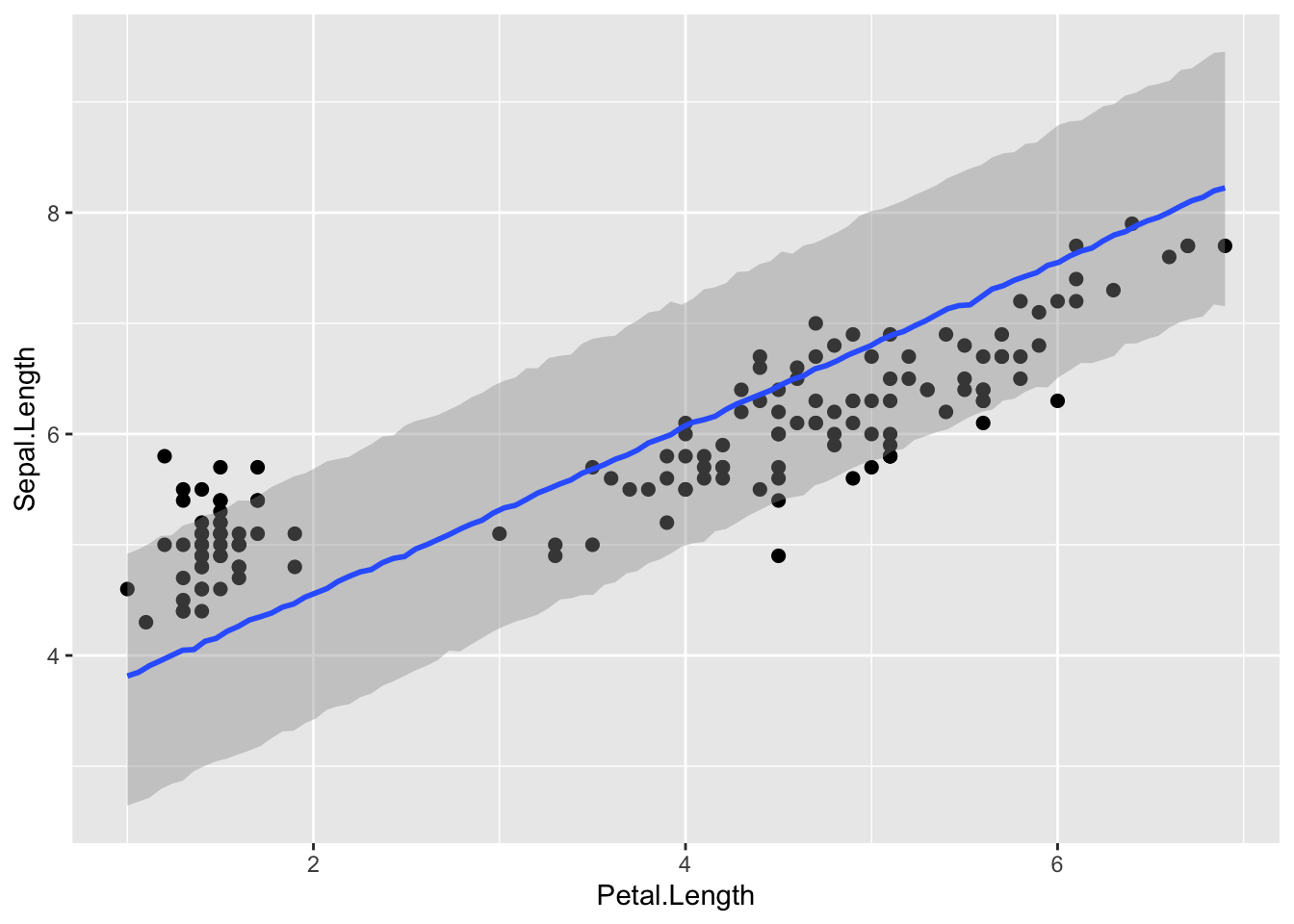

Ennustus on selles mõttes ok, et vaid väike osa punkte jääb sellest välja, aga laiavõitu teine!

Nüüd ennustame sama mudeli põhjal igale liigile eraldi. Seega kasutame mudeli madalama taseme koefitsiente. Peame andma lisaparameetri re_formula = NULL, mis tagab, et ennustuse tegemisel kasutatakse ka mudeli madalama taseme koefitsiente.

plot(marginal_effects(m2, effects = "Petal.Length", method = "predict", conditions = make_conditions(iris, vars = "Species"), probs = c(0.1, 0.9), re_formula = NULL), points = TRUE)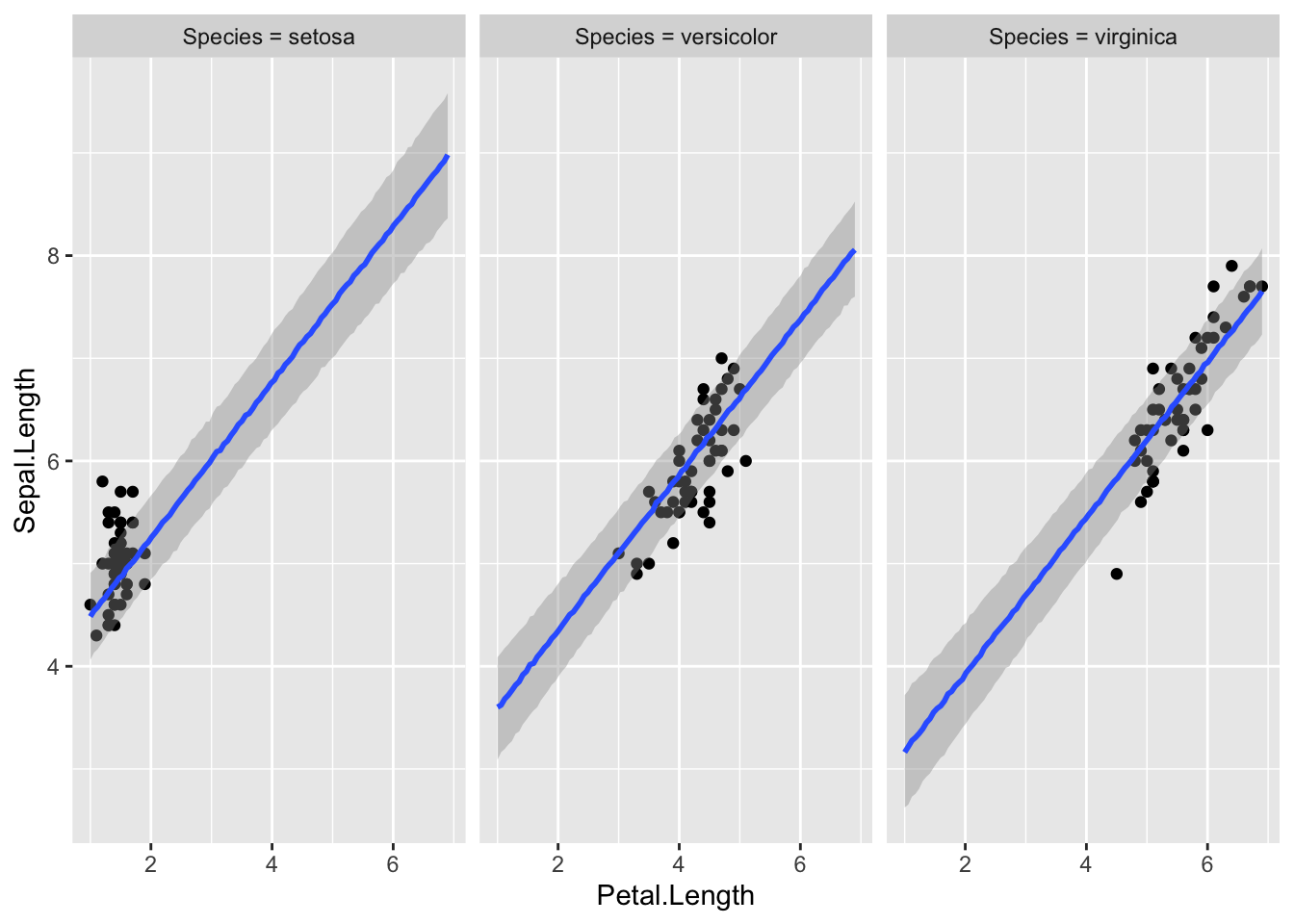

method = "predict" ennustab, millisesse vahemikku peaks mudeli järgi jääma 90% andmepunkte (k.a. uued andmepunktid, mida pole veel valimisse korjatud).

Tõesti, valdav enamus valimi punkte on intervallis sees, mis viitab et mudel töötab hästi. Seal, kus on rohkem punkte, on intervall kitsam ja mudel usaldusväärsem.

Järgneval pildil on method = "fitted". Nüüd on enamus punkte väljaspool usaldusintervalle, mis sellel pildil mõõdavad meie usaldust regressioonijoone vastu.

plot(marginal_effects(m2, effects = "Petal.Length", method = "fitted", conditions = make_conditions(iris, vars = "Species"), probs = c(0.1, 0.9), re_formula = NULL), points = TRUE)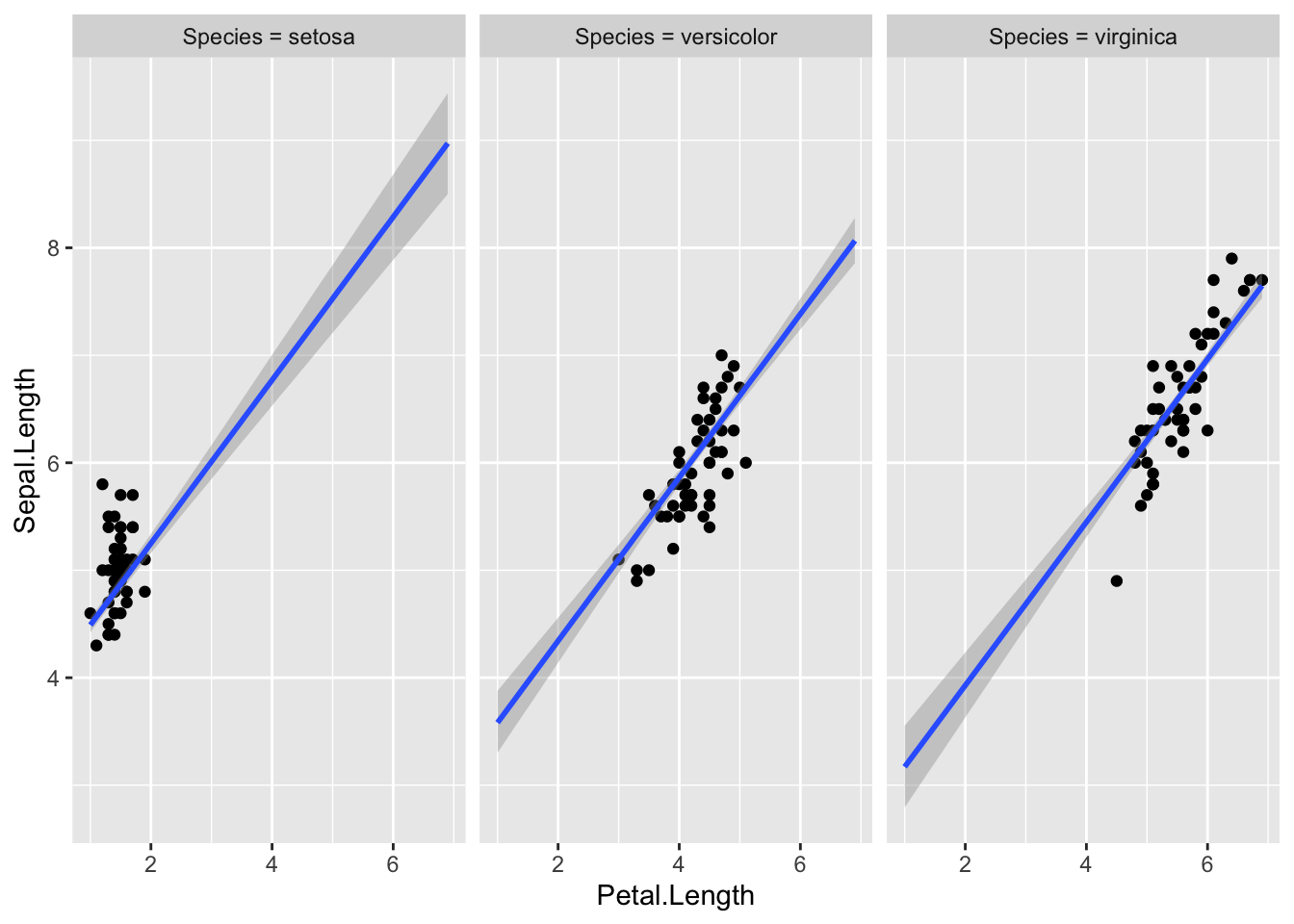

method = "fitted" annab CI regressioonijoonele.

Argumendid:

method – predict annab veapiirid (95% CI) mudeli ennustustustele andmepunkti tasemel. fitted annab veapiirid mudeli fitile endale (joonele, mis tähistab keskmist või kõige tõenäolisemat y muutuja väärtust igal x-i väärtusel)
conditions - andmeraam, kus on kirjas mudeli nendele ennustavatele (x) muutujatele omistatud väärtused, mida ei joonistata x teljele. Kuna meil on selleks mudeli madalama taseme muutuja Species, siis on lisaks vaja määrata argument re_formula = NULL, mis tagab, et ennustuste tegemisel kasutatakse mudeli kõikide tasemete fititud koefitsiente. re_formula = NA annab seevastu keskmise fiti üle kõigi gruppide (irise liikide)
probs annab usaldusintervalli piirid.

Pane tähele, et argument points (ja muud lisaargumendid, nagu näiteks theme) kuuluvad plot(), mitte marginal_effects() funktsioonile.

Tavaline interaktsioonimudel, aga pidevatele muutujatele.

m5 <- brm(Sepal.Length ~ Petal.Length + Sepal.Width + Petal.Length * Sepal.Width, 
          data = iris, 
          prior = prior, 
          family = gaussian)
write_rds(m5, path = "data/m5.fit")

Kõigepealt plotime mudeli ennustused, kuidas Sepal Length sõltub Petal Length-ist kolmel erineval Sepal width väärtusel.

plot(marginal_effects(m5, effects = "Petal.Length:Sepal.Width"), points = TRUE)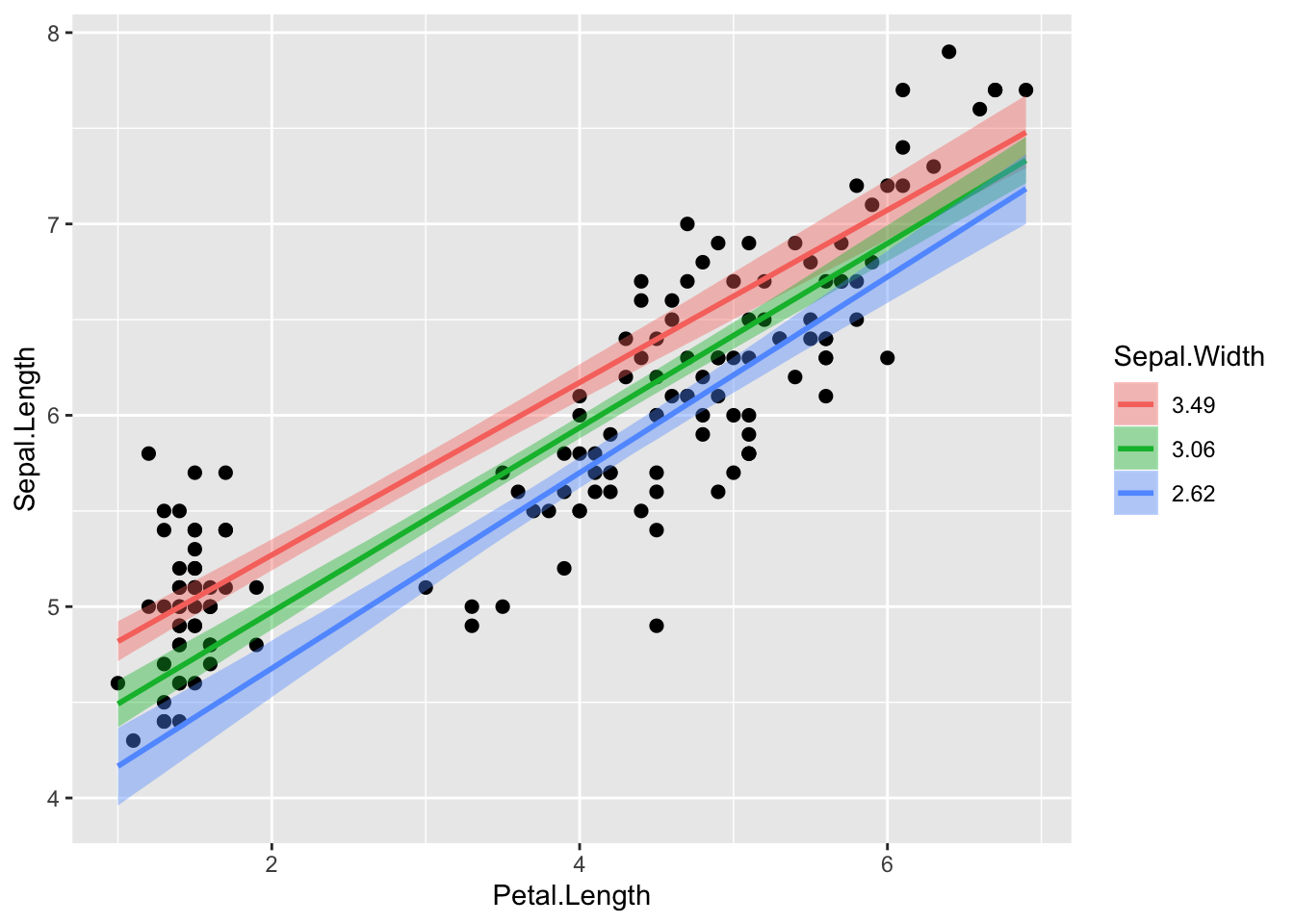

Ja siis sümmeetriliselt vastupidi.

plot(marginal_effects(m5, effects = "Sepal.Width:Petal.Length"), points = TRUE)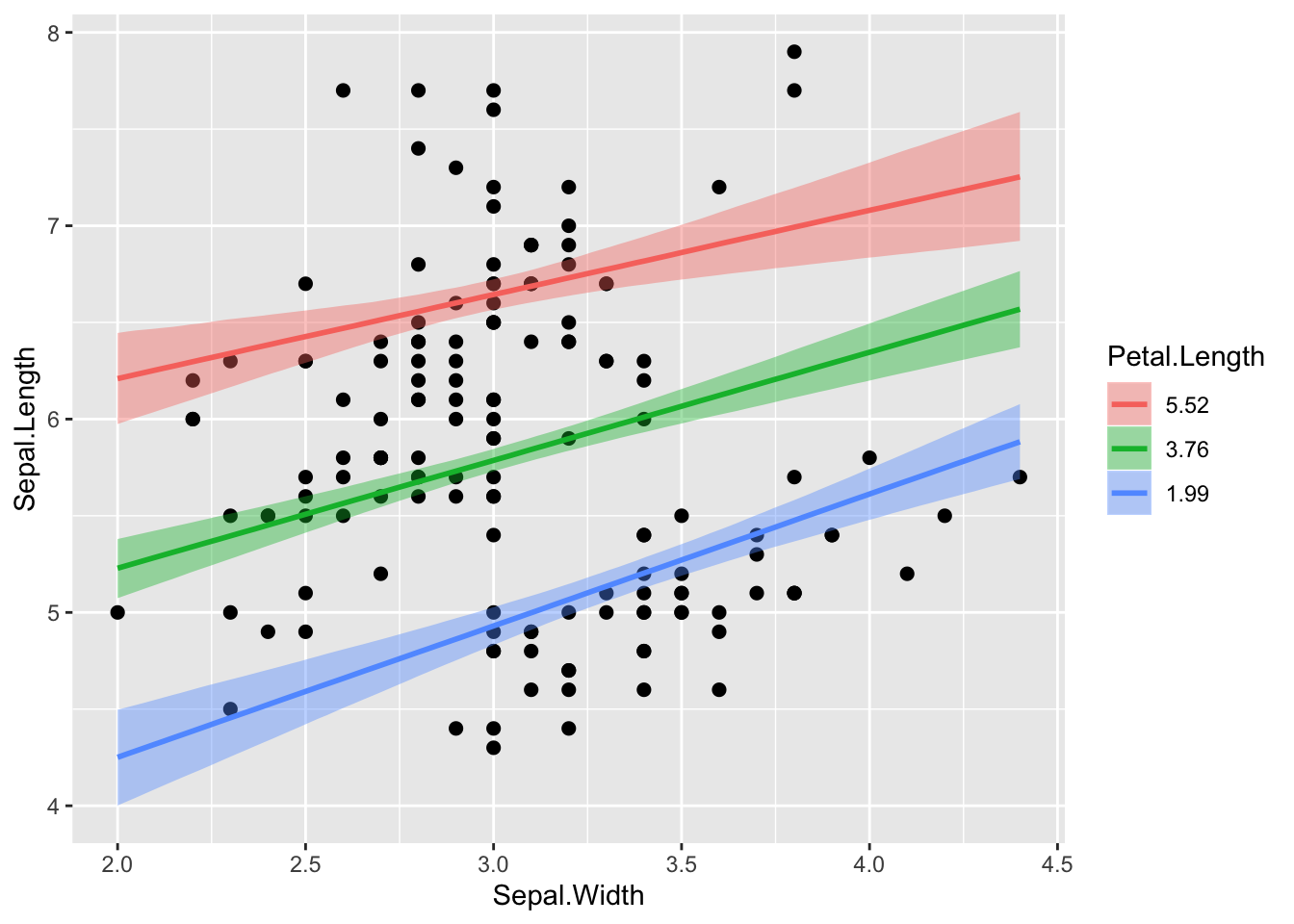

Siin lisame enda soovitud Sepal Width väärtused (5 ja 1.2), mis on väljaspool seda, mida loodus pakub. Pane tähele ennustuse laiemaid CI-e.

conditions <- data.frame(Sepal.Width = c(5, 1.2))
plot(marginal_effects(m5, effects = "Petal.Length", conditions = conditions, re_formula = NULL), points = TRUE)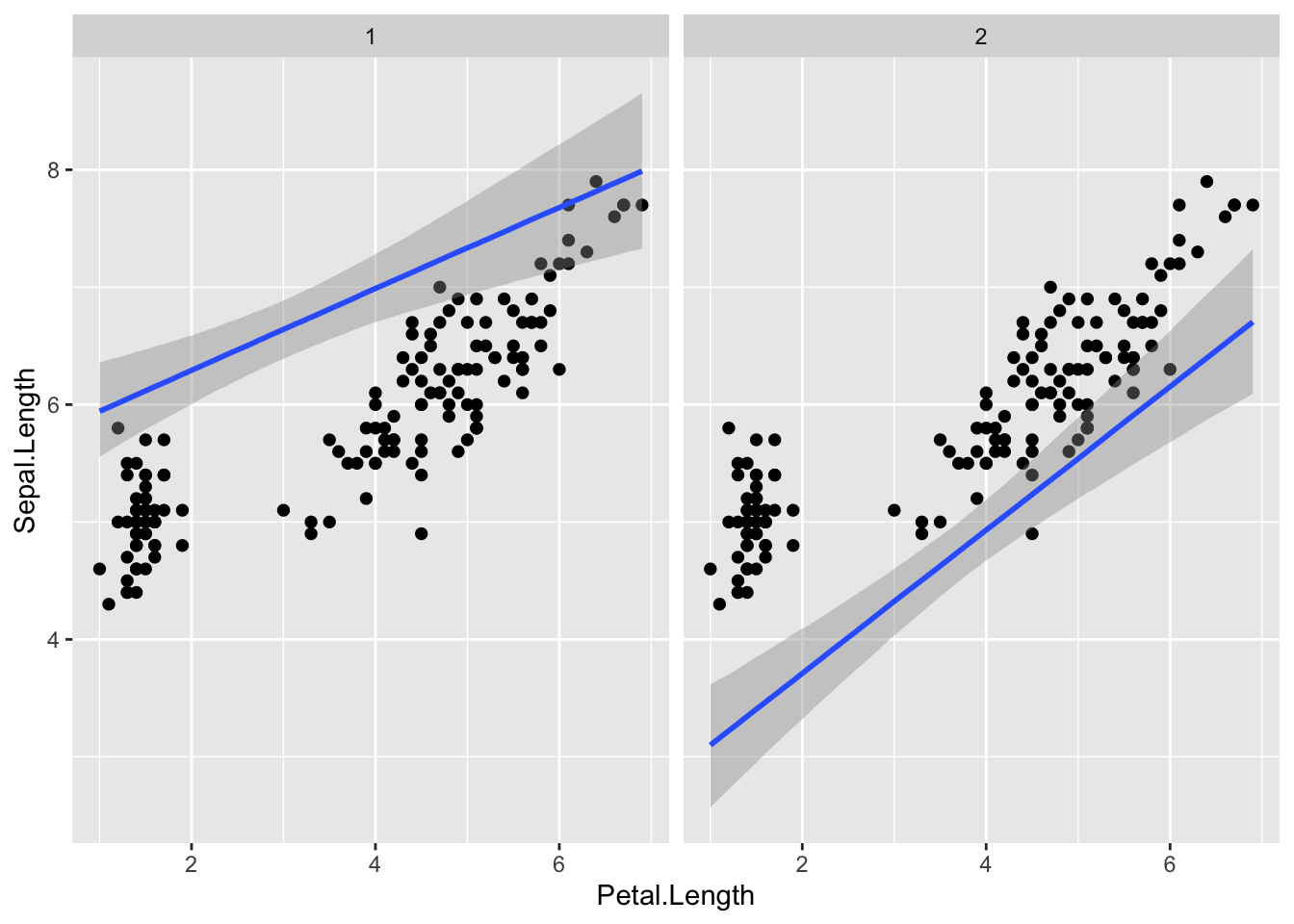

21.1.12 Alternatiivne tee

Alternatiivne millele? Teeme tabeli nende väärtustega, millele tahame mudeli ennustusi. Tabelis newx on spetsifitseeritud mudeli kõikide X muutujate väärtused! Me ennustame Y väärtusi paljudel meie poolt võrdse vahemaaga ette antud petal length väärtustel, kusjuures me hoiame sepal width väärtuse alati konstantsena tema valimi keskmisel väärtusel ja vaatame ennustusi eraldi kahele liigile kolmest. Liigid on mudeli madala taseme osad, seega kasutame ennustuste tegemisel mudeli kõikide tasemete koefitsiente.

newx <- expand.grid(Petal.Length = modelr::seq_range(iris$Petal.Length, n = 150),
                    Sepal.Width = mean(iris$Sepal.Width),
                    Species = c("setosa", "virginica"))

expand.grid() lõõb tabeli pikaks nii, et kõik võimalikud kombinatsioonid 3st muutujast on täidetud väärtustega.

re_formula NULL mudeldab eraldi liigid eraldi mudeli madalama taseme (liikide sees) koefitsiente kasutades

predict_interval_brms2 <- predict(m2, newdata = newx, re_formula = NULL) %>%
  cbind(newx, .)
head(predict_interval_brms2)
#>   Petal.Length Sepal.Width Species Estimate Est.Error Q2.5 Q97.5
#> 1         1.00        3.06  setosa     4.49     0.321 3.85  5.11
#> 2         1.04        3.06  setosa     4.52     0.322 3.91  5.13
#> 3         1.08        3.06  setosa     4.55     0.318 3.93  5.15
#> 4         1.12        3.06  setosa     4.58     0.314 3.96  5.20
#> 5         1.16        3.06  setosa     4.62     0.317 4.00  5.23
#> 6         1.20        3.06  setosa     4.65     0.316 4.04  5.27

predict() ennustab uusi petal length väärtusi (Estimate veerg) koos usaldusinetrvalliga neile väärtustele

Siin siis eraldi ennustused kahele liigile kolmest, kaasa arvatud petal length väärtusvahemikule, kus selle liigi isendeid valimis ei ole (ja võib-olla ei saagi olla)

no_versicolor <- filter(iris, Species != "versicolor")
ggplot(data = predict_interval_brms2, aes(x = Petal.Length, y = Estimate)) +
  geom_point(data = no_versicolor, aes(Petal.Length, Sepal.Length, color = Species)) +
  geom_line(aes(color = Species)) +
  geom_ribbon(aes(ymin = Q2.5, ymax = Q97.5, fill = Species), alpha = 1/3)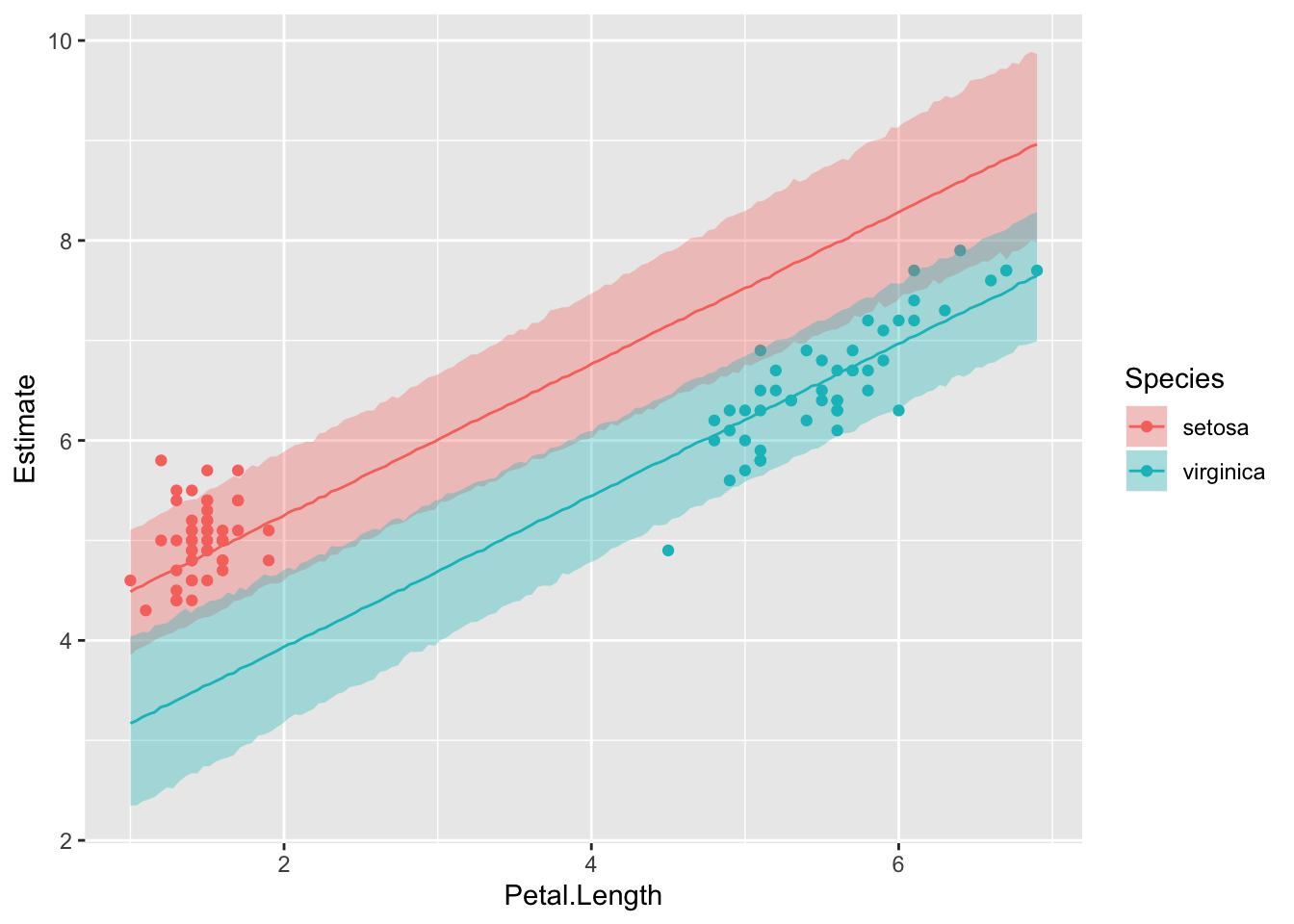

Ennustav plot - kuidas lähevad kokku mudeli ennustused reaalsete y-i andmepunktidega?

NB! Tähtis on alati plottida mudeli ennustus y teljele. Vastupidi plottides ei jää ka ideaalsed ennustused intercept = 0, slope = 1 joonele.

pr <- predict(m2) %>% cbind(iris)
ggplot(pr, aes(Sepal.Length, Estimate, color = Species)) +
  geom_pointrange(aes(ymin = Q2.5, ymax = Q97.5)) +
  geom_abline(lty = 2) +
  coord_cartesian(xlim = c(4, 8), ylim = c(4, 8))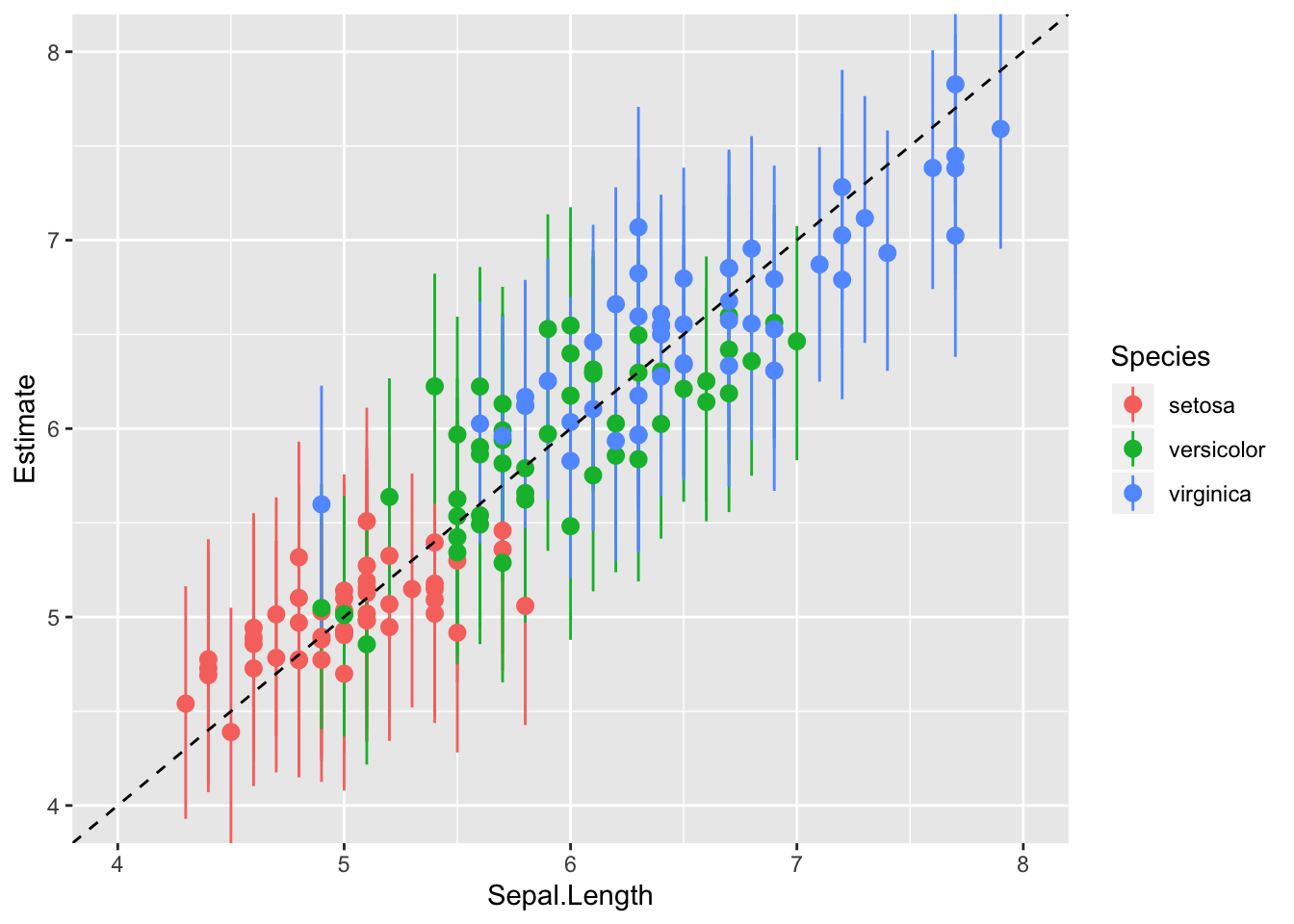

Igale andmepunktile – kui palju erineb selle residuaal 0-st kui hästi ennustab mudel just seda andmepunkti. Ruumi kokkuhoiuks plotime välja ainult irise valiku 50-st andmepunktist.

set.seed(69)
as_data_frame(residuals(m2)) %>% 
  sample_n(50) %>% 
  ggplot(aes(x = reorder(seq_along(Estimate), Estimate), y = Estimate)) +
  geom_pointrange(aes(ymin = Q2.5, ymax = Q97.5), fatten = 0.1) +
  coord_flip() +
  theme(text = element_text(size = 8), axis.title.y = element_blank()) +
  xlab("Residuals (95 CI)")
#> Warning: `as_data_frame()` is deprecated, use `as_tibble()` (but mind the new semantics).
#> This warning is displayed once per session.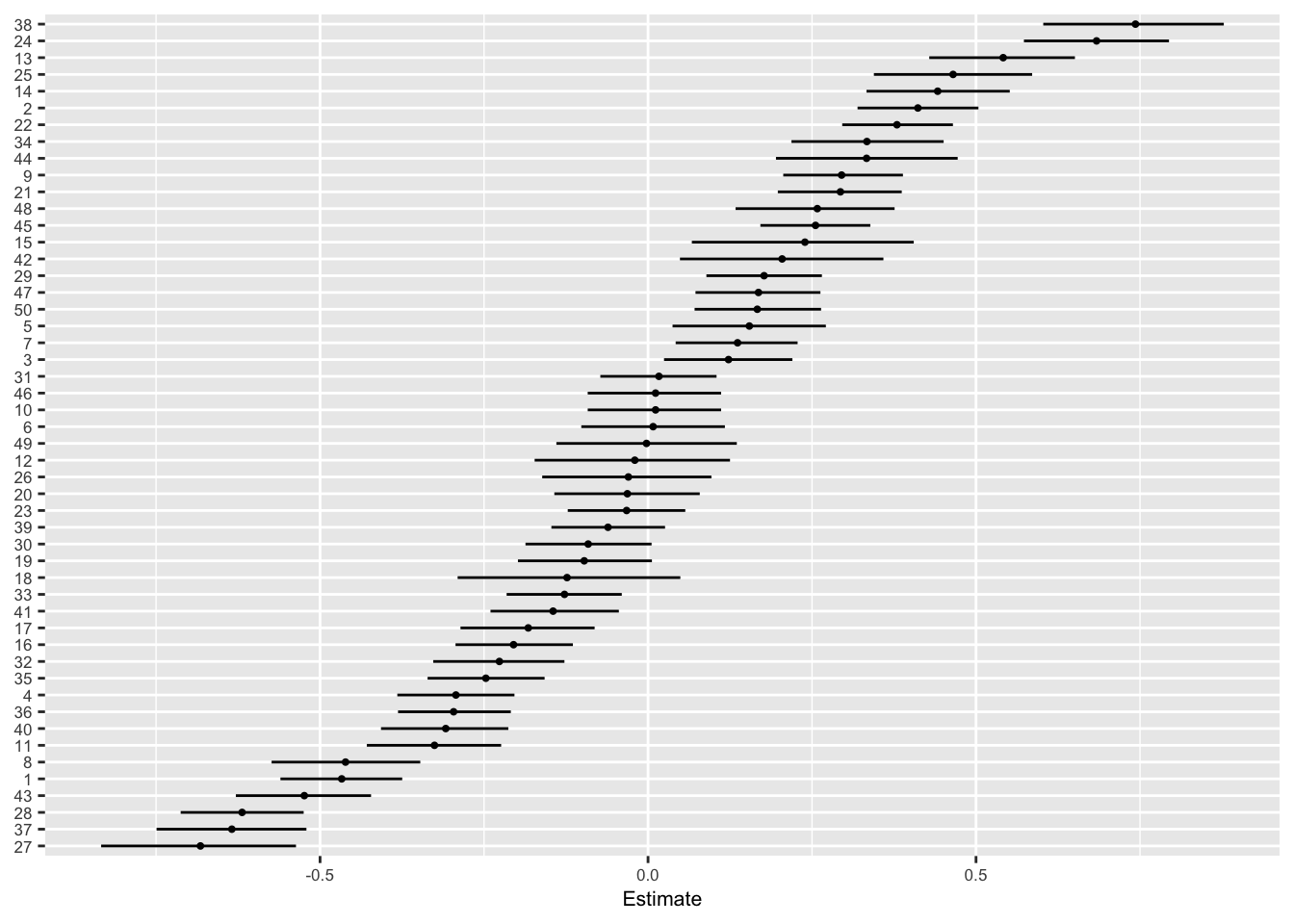

Ok, isendid nr 15 ja 44 paistavad olema vastavalt palju suurema ja väiksema Sepal Lengthiga kui mudel ennustab. Võib küsida, miks?

Nüüd plotime usaldusintervalli mudeli fitile (‘keskmisele’ Y väärtusele igal määratud X-i väärtusel), mitte Y-ennustusele andmepunkti kaupa. Selleks on hea fitted() funktsioon. Me ennustame m2 mudelist vastavalt newdata parameetriväärtustele. Kui me newdata argumendi tühjaks jätame, siis võtab fitted() selleks automaatselt algse iris tabeli (ehk valimi väärtused).

predict_interval_brms2f <- fitted(m2, newdata = newx, re_formula = NULL) %>%
  cbind(newx,.)
head(predict_interval_brms2f)
#>   Petal.Length Sepal.Width Species Estimate Est.Error Q2.5 Q97.5
#> 1         1.00        3.06  setosa     4.49    0.0542 4.38  4.59
#> 2         1.04        3.06  setosa     4.52    0.0535 4.41  4.62
#> 3         1.08        3.06  setosa     4.55    0.0529 4.45  4.65
#> 4         1.12        3.06  setosa     4.58    0.0524 4.48  4.68
#> 5         1.16        3.06  setosa     4.61    0.0520 4.51  4.71
#> 6         1.20        3.06  setosa     4.64    0.0518 4.54  4.74

ggplot(data = predict_interval_brms2f, aes(x = Petal.Length, y = Estimate, color = Species)) +
  geom_point(data = no_versicolor, aes(Petal.Length, Sepal.Length, color = Species)) +
  geom_line() +
  geom_ribbon(aes(ymin = Q2.5, ymax = Q97.5, fill = Species), alpha = 1/3, colour = NA) +
  scale_x_continuous(breaks = 0:10)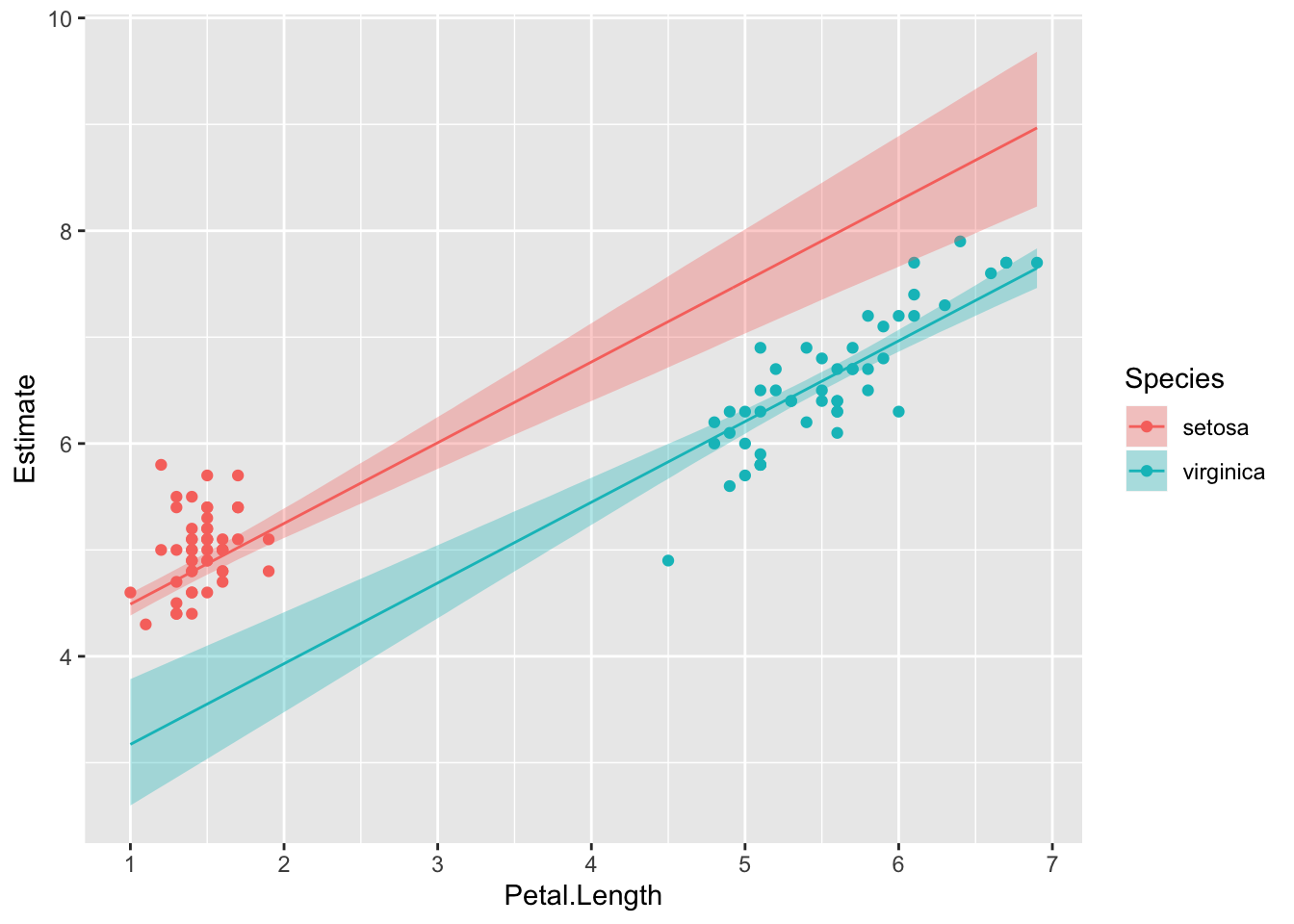

Mudeli genereeritud andmed ja valimiandmed mõõtmisobjekti (subjekti e taimeisendi) kaupa. See on sisuliselt posterior predictive plot (vt eespool).

predicted_subjects_brms <- predict(m2) %>% cbind(iris, .)

predict() arvutab mudeli põhjal uusi Y muutuja andmepunkte. Võib kasutada ka väljamõeldud andmete pealt Y väärtuste ennustamiseks (selleks tuleb anda ette andmeraam kõigi X-muutujate väärtustega, mille pealt tahetakse ennustusi).

Punktid on ennustused ja ristikesed on valimiandmed

ggplot(data = predicted_subjects_brms, aes(x = Petal.Length, color = Species)) +
  geom_point(aes(y = Estimate)) +
  geom_point(aes(y = Sepal.Length), shape = 3)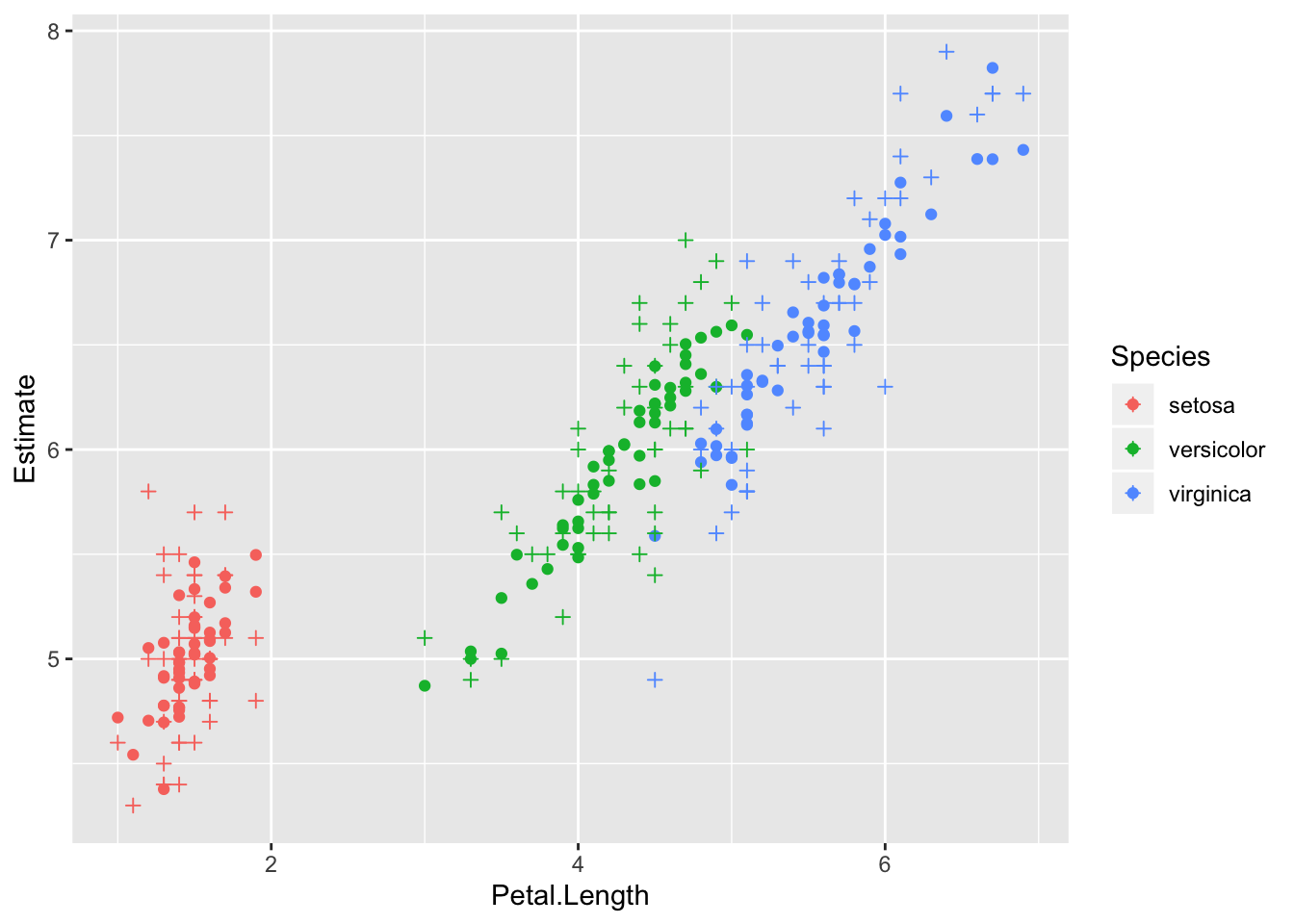

21.1.13 Alternatiiv – ansambliennustus

Kuna meil on 2 mudelit (m2 ja m3) mis on pea võrdselt eelistatud, siis genreerime ennustused mõlemast (mudelite ansamblist) proportsionaalselt nende waic skooridega. See ennustus kajastab meie mudeldamistööd tervikuna, mitte ühte “parimat” mudelit ja seega võib loota, et annab paremini edasi meie mudeldamises peituvat ebakindlust.

pp_a <- pp_average(m2, m3, weights = "waic", method = "predict") %>%
  as_tibble() %>% 
  bind_cols(iris)
ggplot(data = pp_a, aes(x = Petal.Length, color = Species)) +
  geom_point(aes(y = Estimate)) +
  geom_point(aes(y = Sepal.Length), shape = 3)

21.2 Mudeli eelduste kontroll

Pareto k otsib nn mõjukaid (influential) andmepunkte.

loo_m2 <- loo(m2)
plot(loo_m2)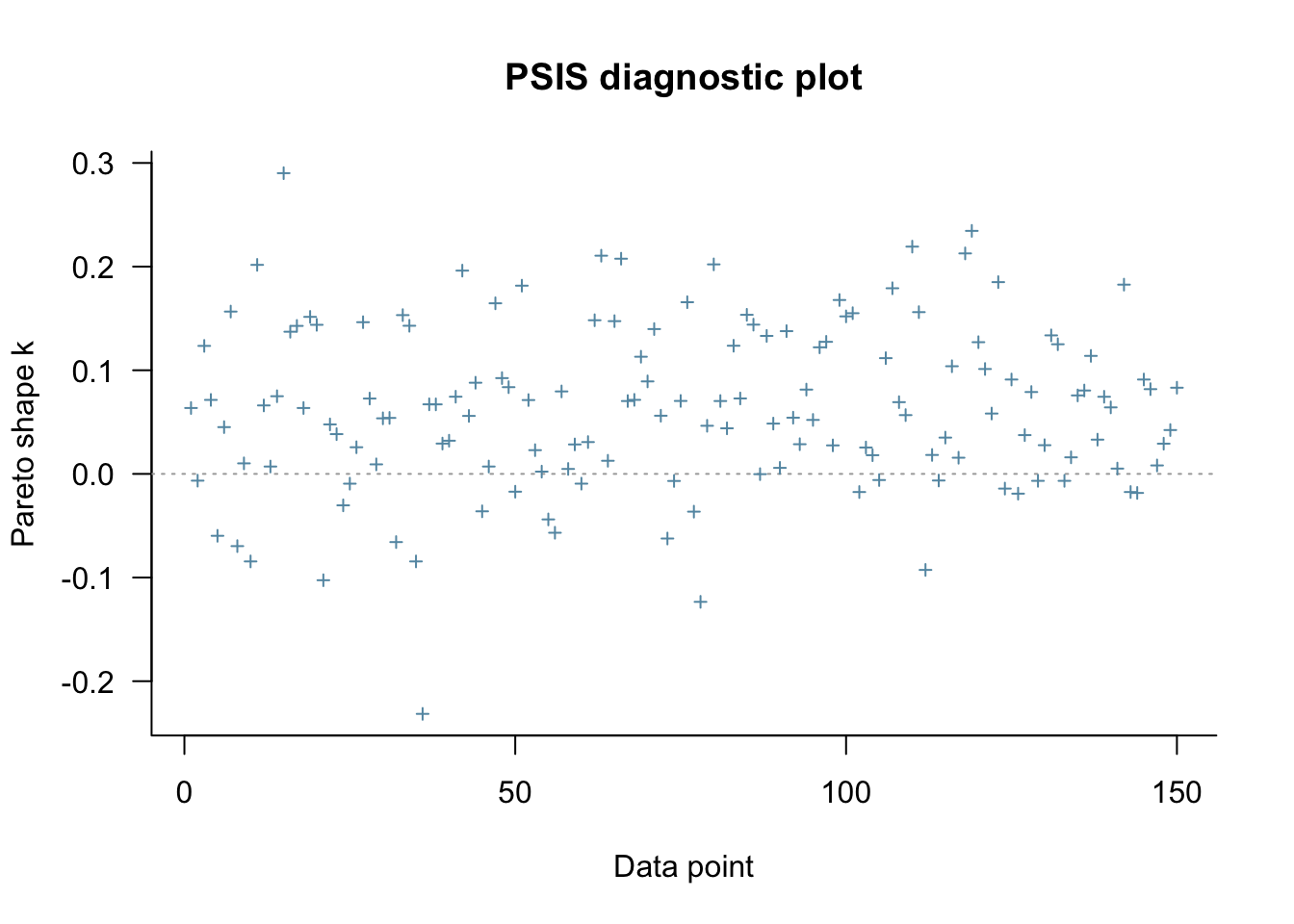

Kui paljud andmepunktid on kahtlaselt mõjukad?

pareto_k_table(loo_m2) 
#> 
#> All Pareto k estimates are good (k < 0.5).

21.2.1 Plotime residuaalid

resid() annab residuaalid vektorina. Kõigepealt plotime residuaalid fititud (keskmiste) Y väärtuste vastu:

resid <- residuals(m2, type = "pearson")
fit <- fitted(m2)
ggplot() + 
  geom_point(aes(x = fit[,"Estimate"], y = resid[,"Estimate"])) + 
  geom_hline(yintercept = 0, lty = "dashed") +
  labs(x = "fitted", y = "residuals")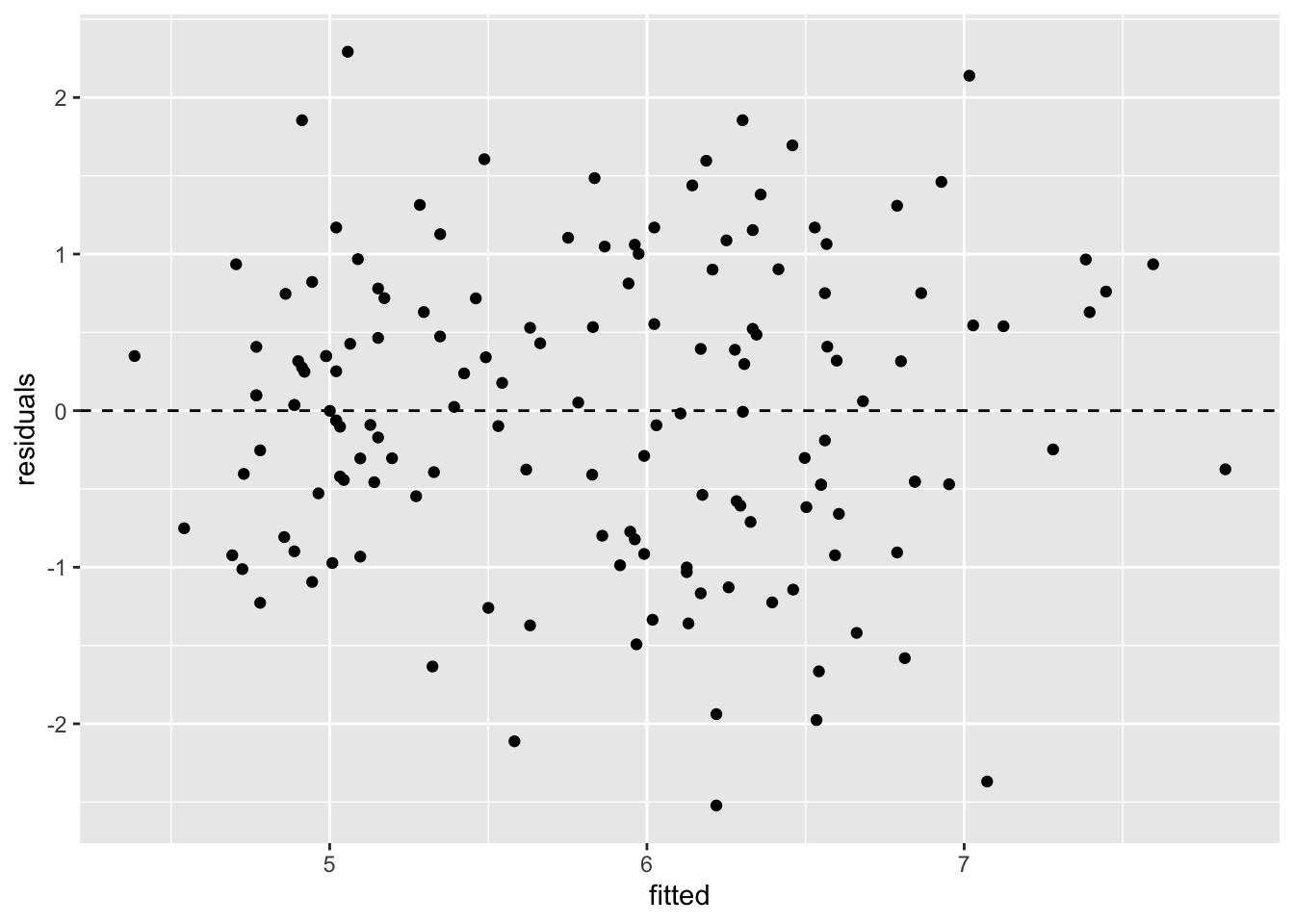

type = "pearson" annab standardiseeritud residuaalid $R = (Y - Y_p) / SD(Y)$, kus SD(Y) on hinnang Y-muutuja SD-le. alternatiiv on type = "ordinary", mis annab tavalised residuaalid.

Residuals vs fitted plot testib lineaarsuse eeldust - kui .resid punktid jaotuvad ühtlaselt nulli ümber, siis mudel püüab kinni kogu süstemaatilise varieeruvuse teie andmetest ja see mis üle jääb on juhuslik varieeruvus.

Vaatame diagnostilist plotti autokorrelatsioonist residuaalide vahel.

acf(resid[,1])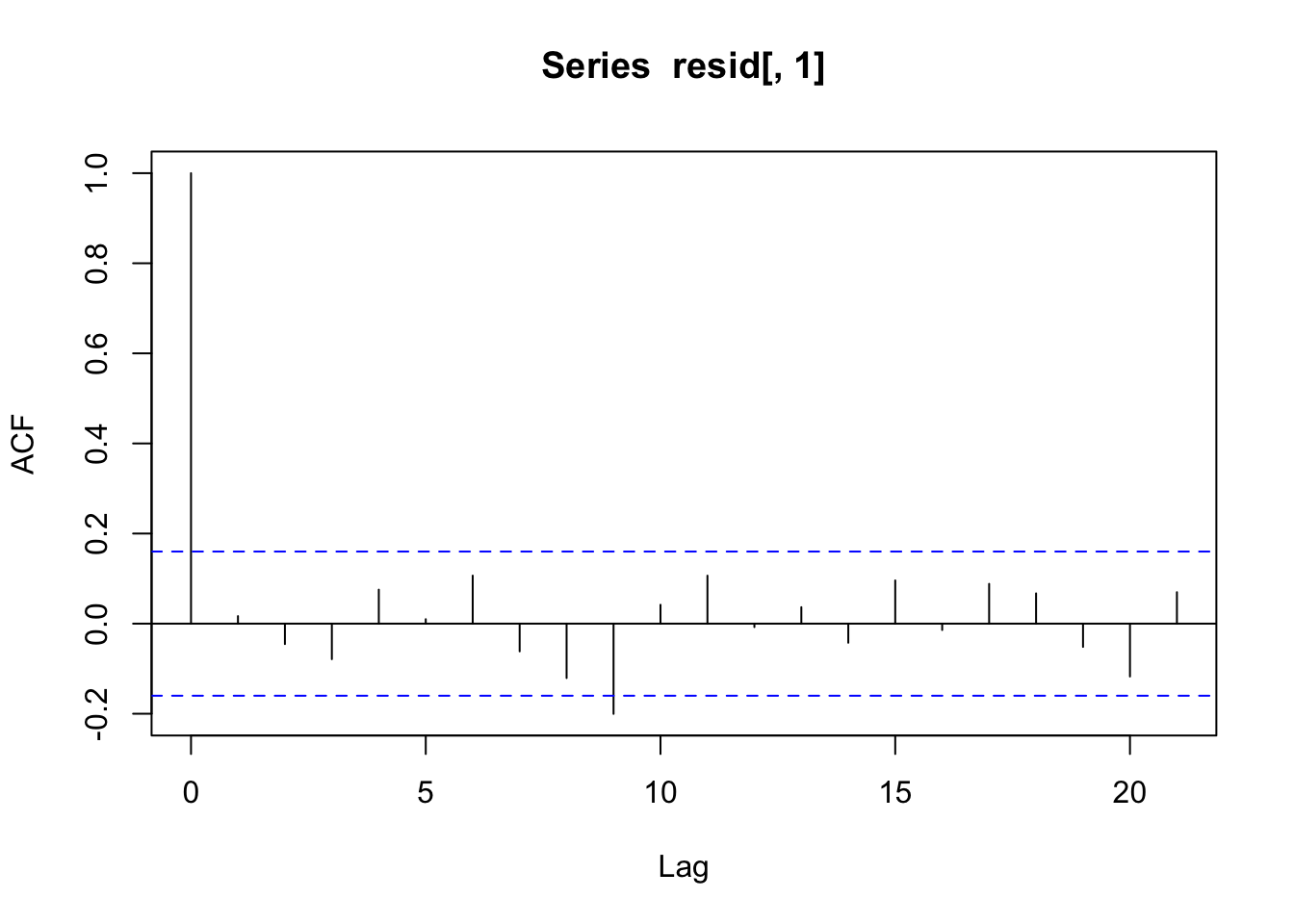

Residuaalide autokorrelatsioonid on madalad - seega kõik paistab OK ja andmepunktide sõltumatus on tagatud.

Siin on residuaalide histogramm:

ggplot(data = NULL) + 
  geom_density(aes(x = resid[,"Estimate"]), fill = "lightgrey") + 
  geom_vline(xintercept = median(resid), linetype = "dashed")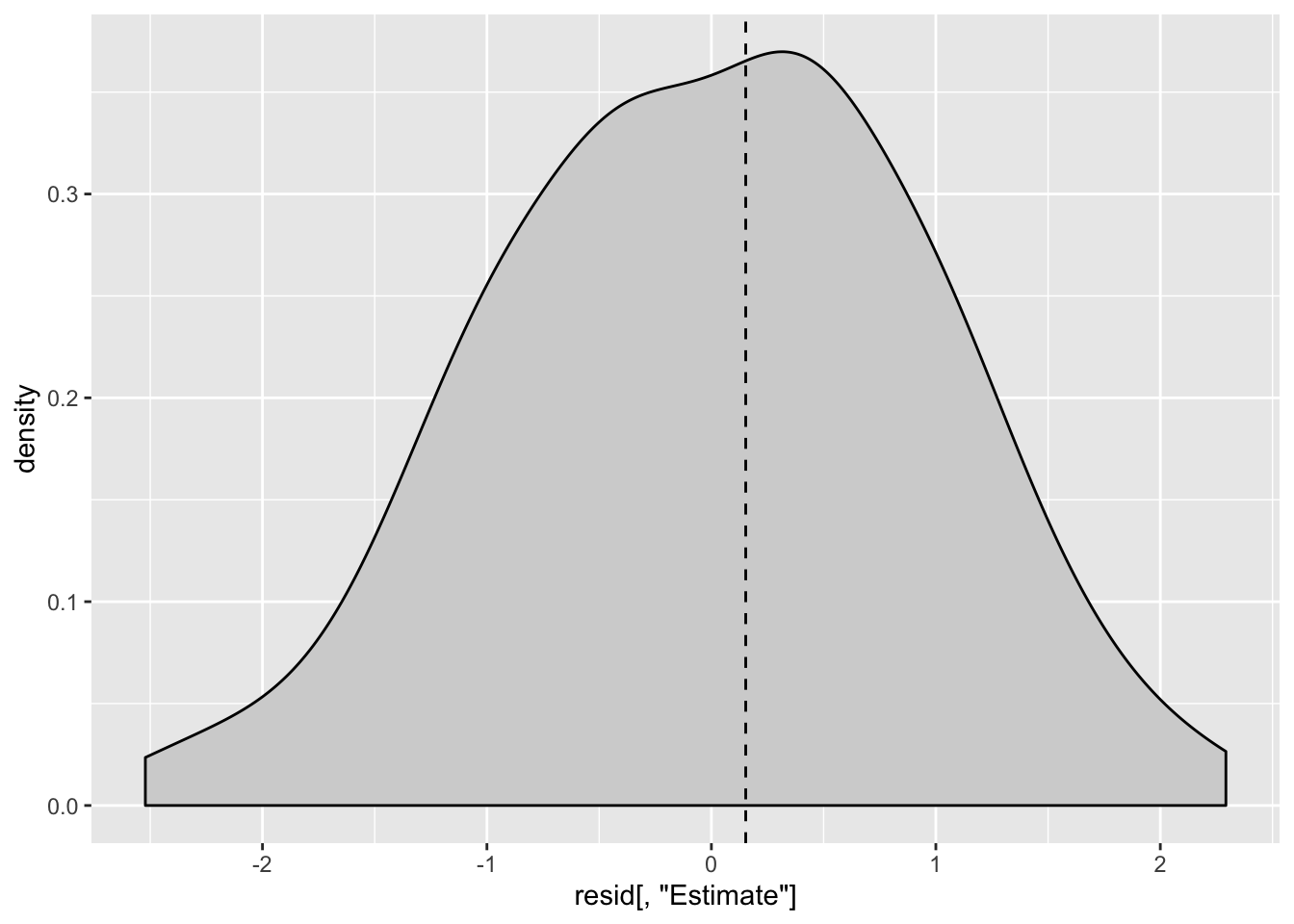

Residuaalid on sümmeetrilise jaotusega ja meedian residuaal on peaaegu null. See on kõik hea.

Ja lõpuks plotime standardiseeritud residuaalid kõigi x-muutujate vastu. Kõigepealt ühendame resid vektori irise tabeliga, et oleks mugavam plottida. residuaalid standardhälbe ühikutes saab ja ka tuleks plottida kõigi x-muutujate suhtes.

iris2 <- iris %>% cbind(resid)  
ggplot(iris2, aes(Petal.Length, Estimate, color = Species)) + 
  geom_point() +
  geom_hline(yintercept = 0, linetype = "dashed")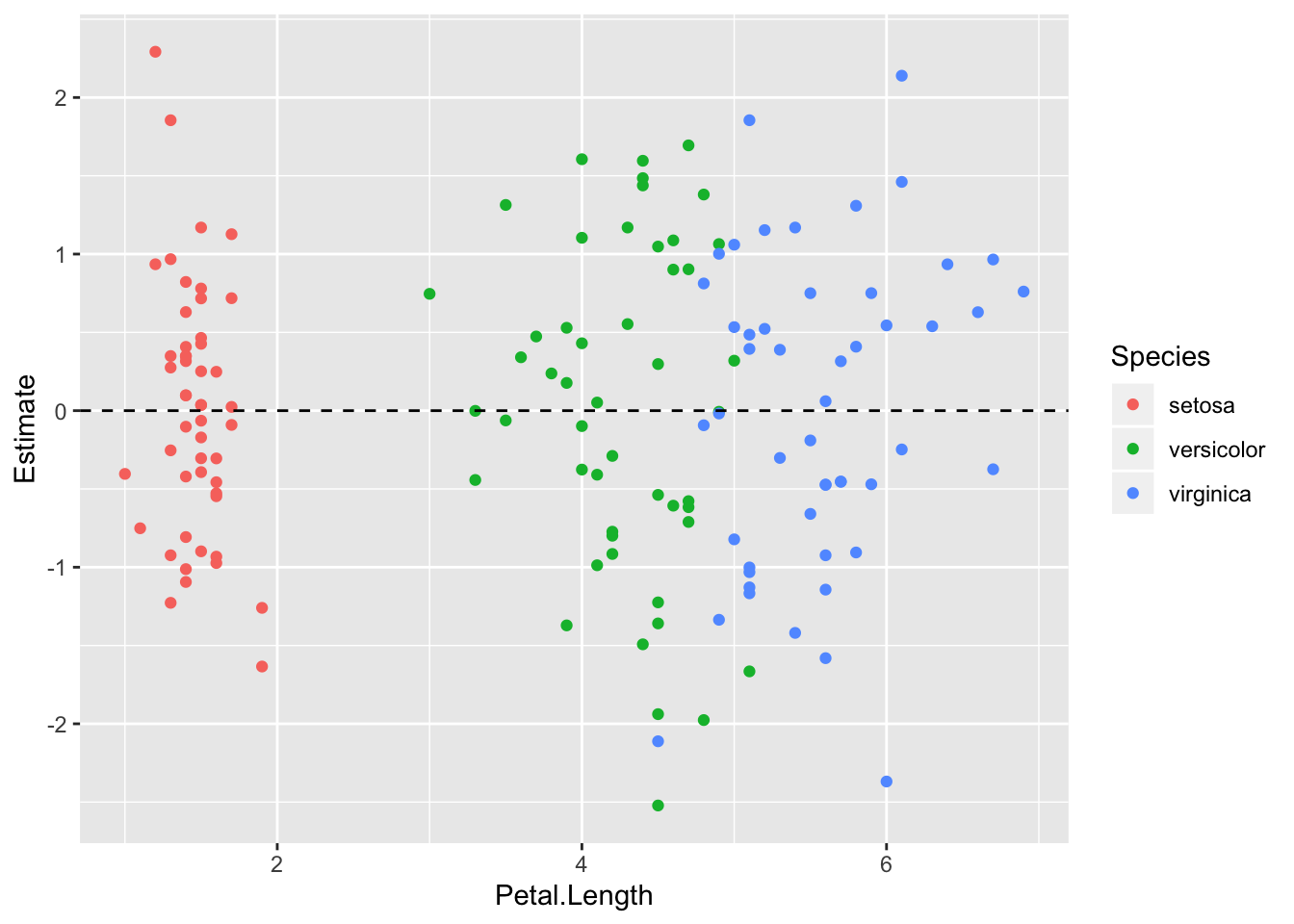

Tsiteerides klassikuid: “Pole paha!”. Mudel ennustab hästi, aga mõne punkti jaoks on ennustus 2 sd kaugusel.

ggplot(iris2, aes(Sepal.Width, Estimate, color = Species)) + 
  geom_point() +
  geom_hline(yintercept = 0, linetype = "dashed")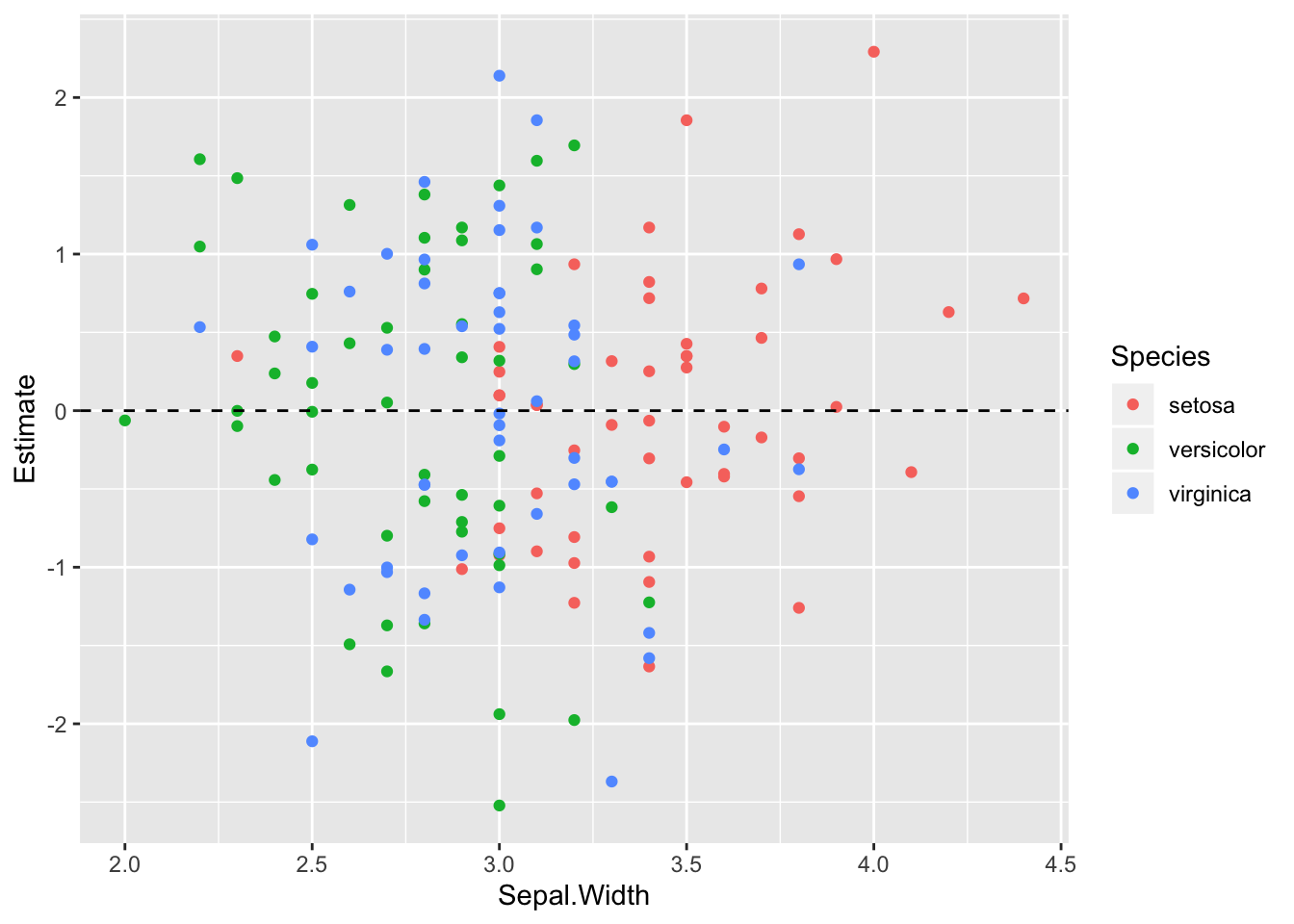

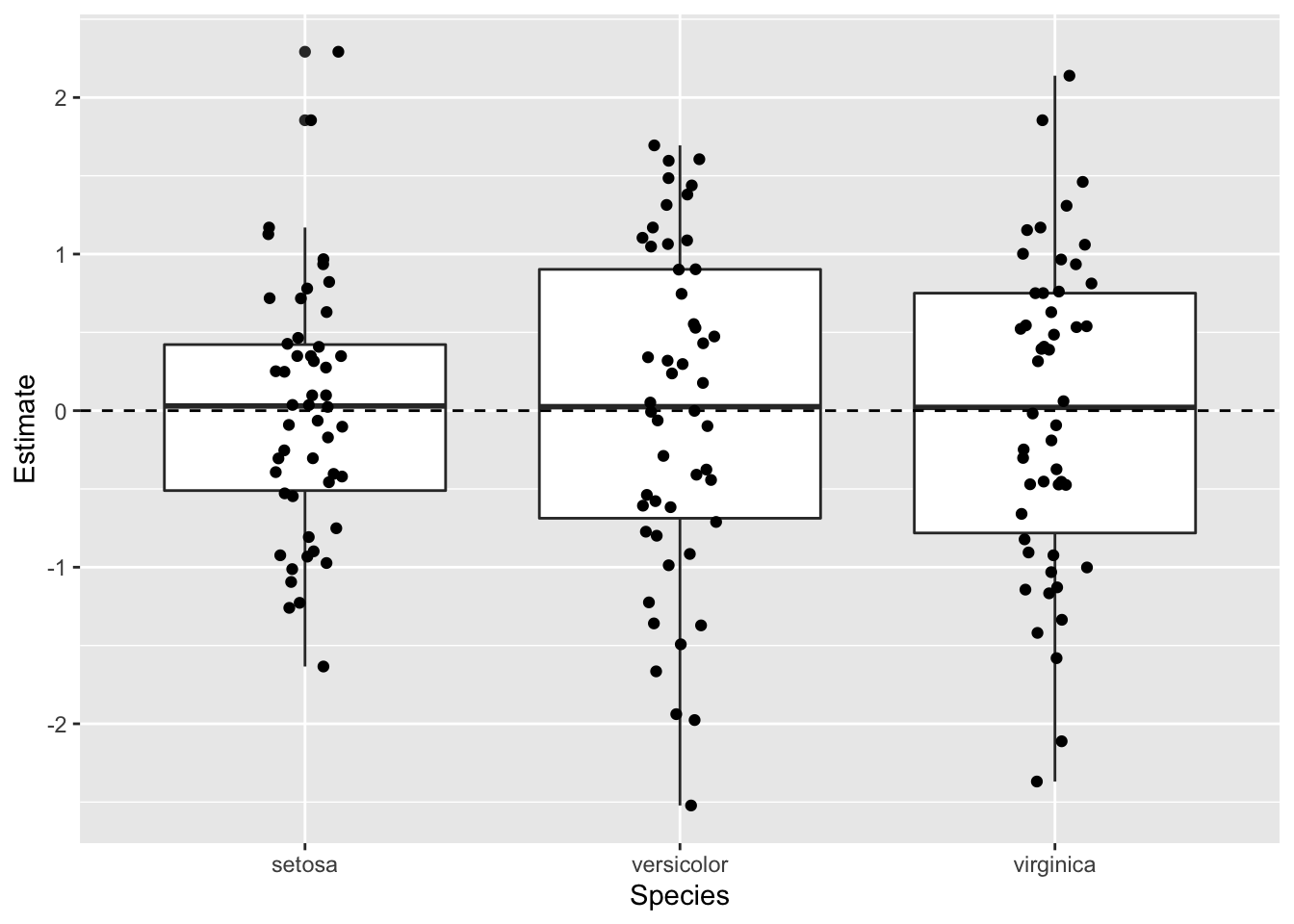
ggplot(iris2, aes(Species, Estimate)) + 
  geom_boxplot() +
  geom_hline(yintercept = 0, linetype = "dashed") +
  geom_jitter(width = 0.1)