12 Bootstrap

library(rethinking)
library(bayesboot)
library(dplyr)
library(purrr)
library(ggplot2)
library(modelr)

Populatsioon on valimile sama, mis on valim bootstrappitud valimile.

Nüüd alustame ühestainsast empiirilisest valimist ja genereerime sellest 2000 virtuaalset valimit. Selleks tõmbame me oma valimist virtuaalselt 2000 uut juhuvalimit (bootstrap valimit), millest igaüks on sama suur kui algne valim. Saladus seisneb selles, et bootstrap valimite tõmbamine käib asendusega, st iga empiirilise valimi element, mis bootstrap valimisse tõmmatakse, pannakse kohe algsesse valimisse tagasi. Seega saab seda elementi kohe uuesti samasse bootstrap valimisse tõmmata (kui juhus nii tahab). Seega sisaldab tüüpiline bootstrap valim osasid algse valimi numbreid mitmes korduses ja teisi üldse mitte. Iga bootstrap valimi põhjal arvutatakse meid huvitav statistik (näiteks keskväärtus) ja kõik need 2000 bootstrapitud statistikut plotitakse samamoodi, nagu me ennist tegime valimitega lõpmata suurest populatsioonist. Ainsad erinevused on, et bootstrapis võrdub andmekogu suurus, millest bootstrap valimeid tõmmatakse, algse valimi suurusega ning, et iga bootstrapi valim on sama suur kui algne valim (sest meie poolt arvutatud statistiku varieeruvus, me tahame oma bootstrap valimiga tabada, sõltub valimi suurusest). Tüüpiliselt kasutatakse bootstrapitud statistikuid selleks, et arvutada usaldusintervall statistiku väärtusele.

Bootstrap ei muuda meie hinnangut statistiku punktväärtusele. Ta annab hinnangu ebakindluse määrale, mida me oma valimi põhjal peaksime tundma selle punkthinnangu kohta.

Bootstrappimine on üldiselt väga hea meetod, mis sõltub väiksemast arvust eeldustest kui statistikas tavaks. Bootstrap ei eelda, et andmed on normaaljaotusega või mõne muu matemaatiliselt lihtsa jaotusega. Tema põhiline eeldus on, et valim peegeldab populatsiooni – mis ei pruugi kehtida väikeste valimite korral ja kallutatud (mitte-juhuslike) valimite korral. Lisaks, tavaline bootstrap ei sobi hierarhiliste andmestruktuuride analüüsiks ega näiteks aegridade analüüsiks. Bootstrappida saab edukalt enamusi statistikuid, mida te võiksite elu jooksul arvutada, aga on siiski erandeid: näiteks valimi maksimum ja miinimumväärtused.

Bootstrap empiirilisele valimile suurusega n töötab nii:

1. tõmba (asendusega) empiirilisest valimist B uut virtuaalset valimit (B bootstrap valimit), igaüks suurusega n.
2. arvuta keskmine, sd või mistahes muu statistik igale bootstrapi valimile. Tee seda B korda.
3. joonista oma statistiku väärtustest histogramm või density plot

Nende andmete põhjal saab küsida palju toreidaid küsimusi — vt allpool.

Mis on USA presidentide keskmine pikkus? Meil on viimase 11 presidendi pikkused.

heights <- tibble(value = c(183, 192, 182, 183, 177, 185, 188, 188, 182, 185, 188))
B <- 1000 # the number of bootstrap samples

mean_value <- function(x) mean(as.data.frame(x)$value, na.rm = TRUE) # helper function
boot <- bootstrap(heights, B)
boot <- boot %>% 
            mutate(Mean = map_dbl(strap, mean_value))

ggplot(boot, aes(Mean)) + geom_density()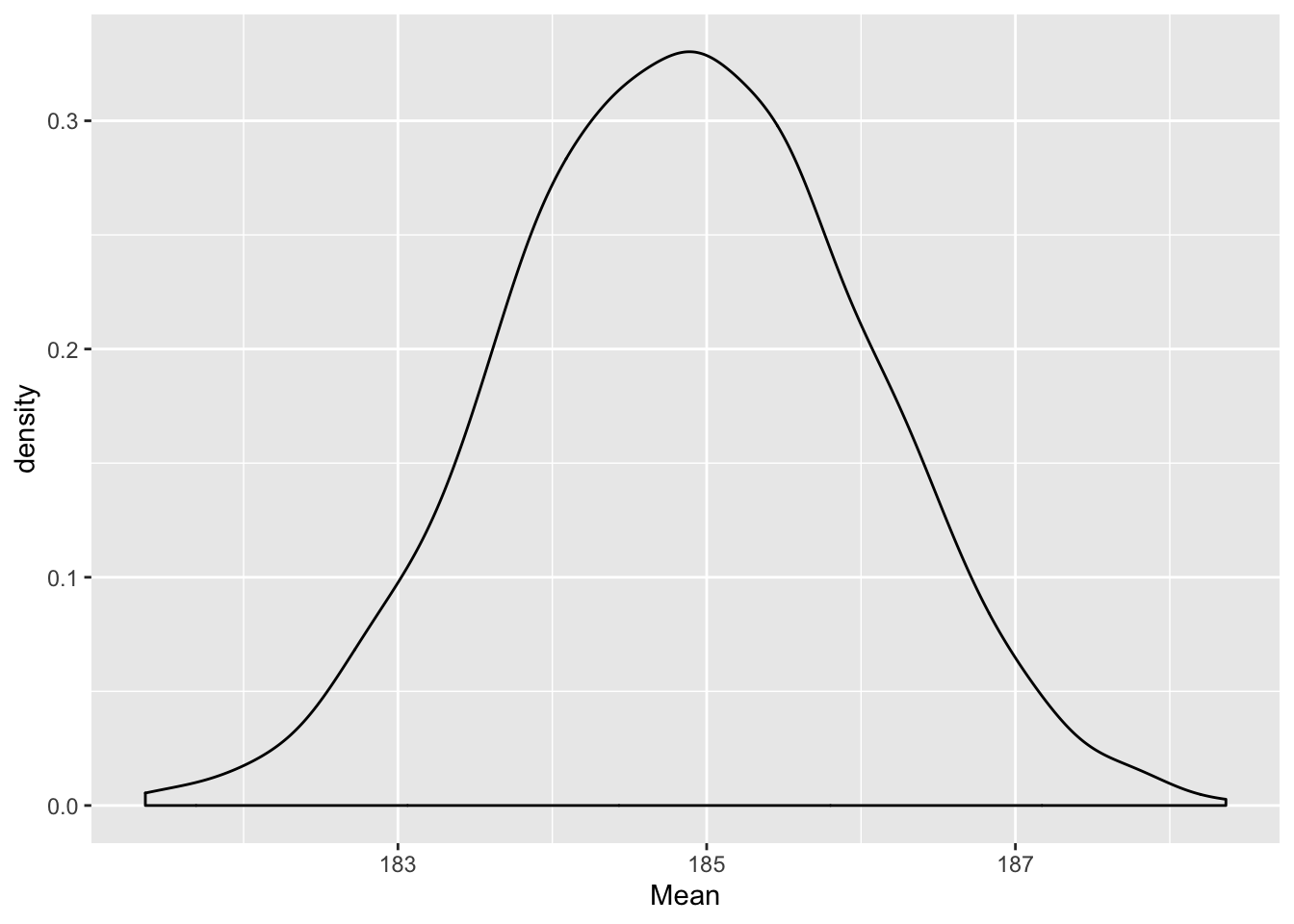

Joonis 12.1: Bootstrapitud posteerior USA presidentide keskmisele pikkusele. Järgnevas koodis ütleme me kõigepealt, et B = 2000 (et me võtame 2000 bootstrap valimit) kasutades selleks broom paketi käsku boot(), millele on lihtne lisada dplyri funktsioon summarise(). Siiski peame seda tegema dplyr::do() abil. Pane tähele, et “tänu” do() kasutamisele peame me summarise() funktsioonis näitama punktiga koha, kuhu lähevad %>% torust tulnud bootstrap valimid. Aga muidu on kõik tavapärane tidyverse.

ehk sama asi ilma bootsrtap functsiooni kasutamata.

heights <- tibble(value = c(183, 192, 182, 183, 177, 185, 188, 188, 182, 185, 188))
n <- nrow(heights) #empirical sample size
B <- 1000 #nr of bootstrap samples
boot1 <-  replicate(B, sample_n(heights, n, replace = TRUE)) 

df22 <- boot1 %>% #boot1 object is a list
  as.data.frame() %>% #convert this list into a data frame 
  summarise_all(mean) %>% t() %>% as_tibble() 

ggplot(df22, aes(V1)) + geom_histogram()

Mida selline keskväärtuste jaotus tähendab? Me võime seda vaadelda posterioorse tõenäosusjaotusena. Selle tõlgenduse kohaselt iseloomustab see jaotus täpselt meie usku presidentide keskmise pikkuse kohta, niipalju kui see usk põhineb bootstrappimises kasutatud andmetel. Senikaua, kui meil pole muud relevantset teavet, on kõik, mida me usume teadvat USA presidentide keskmise pikkuse kohta, peidus selles jaotuses. Need pikkused, mille kohal jaotus on kõrgem, sisaldavad meie jaoks tõenäolisemalt tegelikku USA presidentide keskmist pikkust kui need pikkused, mille kohal posterioorne jaotus on madalam.

Kuidas selle jaotusega edasi töötada? See on lihtne: meil on 2000 arvu (2000 bootstrapitud statistiku väärtust) ja me teeme nendega kõike seda, mida parasjagu tahame.

Näiteks me võime arvutada, millisesse pikkuste vahemikku jääb 92% meie usust USA presidentide tõelise keskmise pikkuse kohta. See tähendab, et teades seda vahemikku peaksime olema valmis maksma mitte rohkem kui 92 senti pileti eest, mis juhul kui USA presidentide keskmine pikkus tõesti jääb sinna vahemikku, toob meile võidu suuruses 1 EUR (ja 8 senti kasumit). Selline kihlveokontor on täiesti respektaabel ja akadeemiline tõenäosuse tõlgendus; see on paljude arvates lausa parim tõlgendus, mis meil on.

Miks just 92% usaldusinterval? Vastus on, et miks mitte? Meil pole ühtegi universaalset põhjust eelistada üht usaldusvahemiku suurust teisele. Olgu meil usaldusinteval 90%, 92% või 95% — tõlgendus on ikka sama. Nimelt, et me usume, et suure tõenäosusega jääb tegelik keskväärtus meie poolt arvutatud vahemikku. Mudeli ja maailma erinevused tingivad niikuinii selle, et konkreetne number ei kandu mudelist otse üle pärismaailma. Eelnevalt mainitud kihlveokontor töötab mudeli maailmas, mitte teie kodulähedasel hipodroomil.

92% usaldusintervalli arvutamiseks on kaks meetodit, mis enamasti annavad vaid veidi erinevaid tulemusi.

1. HPDI — Highest Density Probability Interval — alustab jaotuse tipust (tippudest) ja katab 92% jaotuse kõrgema(te) osa(de) pindalast

HPDI(heights$value, prob = 0.92)
#> |0.92 0.92| 
#>   177   192

2. PI — Probability Interval — alustab jaotuse servadest ja katab kummagist servast 4% jaotuse pindalast. PI 90%-le on sama, mis arvutada 5% ja 95% kvantiilid (jne).

PI(heights$value, prob = 0.90)
#>  5% 95% 
#> 180 190
# quantile(heights$value, probs = c(0.05, 0.95)) teeb sama asja

HPDI on üldiselt parem mõõdik kui PI, aga teatud juhtudel on seda raskem arvutada. Kui HPDI ja PI tugevalt erinevad, on hea mõte piirduda jaotuse enda avaldamisega — jaotus ise sisaldab kogu informatsiooni, mis meil on oma statistiku väärtuse kohta. Intervallid on lihtsalt summaarsed statistikud andmete kokkuvõtlikuks esitamiseks.

Kui suure tõenäosusega on USA presidentide keskmine pikkus suurem kui USA populatsiooni meeste keskmine pikkus (178.3 cm mediaan)?

mean(heights$value > 178.3)
#> [1] 0.909

Ligikaudu 100% tõenäosusega (valimis on 1 mees alla 182 cm, ja tema on 177 cm). Lühikesed jupatsid ei saa Ameerikamaal presidendiks!

Kuidas lahendada bootstrap, kui mei tahame usaldusintervalle kahe ebavõrdse grupi erinevusele? Näiteks kui meil on katsegrupis N = 25 ja kontrollgrupis N = 20, ja me tahame arvutada statistikut ES = katsegrupi keskmine - kontrollgrupi keskmine.

1. tõbma katsegrupist N = 25 bootstrapvalim

2. tõmba kontrollgrupist N = 20 bootsrapvalim

3. lahuta kontrollgrupi bootstrapvalimi mediaan katsegrupi omast (või aritmeetriline keskmine või ükskõik mis muu keskmise näitaja, mida hing ihaldab)

4. korda punkte 1-3 B korda ja tööta edasi bootstrapjaptusega, nagu eespool näidatud.

12.1 Mõned tava-bootstrapi paketid

Professionaalid kasutavad boot paketti, mis on suhteliselt ebameeldiva süntaksiga, aga väga laialt rakendatav. Boot paketi peale on ehitatud tavainimesele hästi kasutatav pakett bootES (Kirby and Gelranc, 2013, Behav Res 45:905–927), mis teeb lihtsaks usalduspiiride leidmise erinevat tüüpi efekti suurustele, kaasa arvatud lihtsad hierarhilised ja ühefaktorilise ANOVA tüüpi katseskeemid. Nendes pakettides tasub üldjuhul kasutada meetodit nimega BCa (bias-corrected-and-accelerated) usalduspiiride arvutamiseks. See meetod püüab parandada bootstrap-valimite võimalikku kallutatust (esineb sedavõrd, kui bootstrap-jaotuse tipp ei ole samas kohas kui oleks paljude päris-valimite pealt arvutatud statistikute jaotuse tipp) ja olukorda, kus statistiku väärtuse varieeruvuse määr sõltub statistiku väärtusest. BCa edukaks arvutamiseks peab bootstrap valimite arv tuntavalt ületama valimi suurust. Simulatsioonidega on näidatud, et BCa (ja teisi) usalduspiire saab mõistlikult arvutada valimitelt, mille suurus on > 15. Sellest väiksemate valimite korral peate eeldama, et teie usaldusinetvallid valetavad. Aegridade, kus esineb järjestikuste ajapunktide vahelisi sõltuvusi, tuleks kasutada nn block bootstrappi, mida implementerrib näiteks boot::tsboot().

Bayesi bootstrap

Kui klassikalise bootstrap meetodi pakkus välja B. Efron aastal 1979, siis selle Bayesi versioon avaldati D.B. Rubini poolt 1981. a. Bayesi versioon bootstrapist on implementeeritud “bayesboot” paketis funktsioonis bayesboot(). Hea lihtsa seletuse Bayesi bootstrapi kohta saab siit https://www.youtube.com/watch?v=WMAgzr99PKE ja lihtsa r koodi selle meetodi rakendamiseks saab siit https://www.r-bloggers.com/simple-bayesian-bootstrap/.

Lühidalt, erinevalt eelkirjeldatud tava-bootstrapist simuleeritakse Bayesi bootstrapis posterioorjaotused, näiteks arvutatakse kaalutud keskmine, kus ühtlasest jaotusest pärit kaalud on prioriks.

Näited sellest, kuidas kasutada bayesbooti standardhälbe, korrelatsioonikoefitsiendi ja lineaarse mudeli koefitsientide usalduspiiride arvutamiseks leiate ?bayesboot käsuga.

heights_bb <- bayesboot(heights$value, mean)
plot(heights_bb, compVal = 185)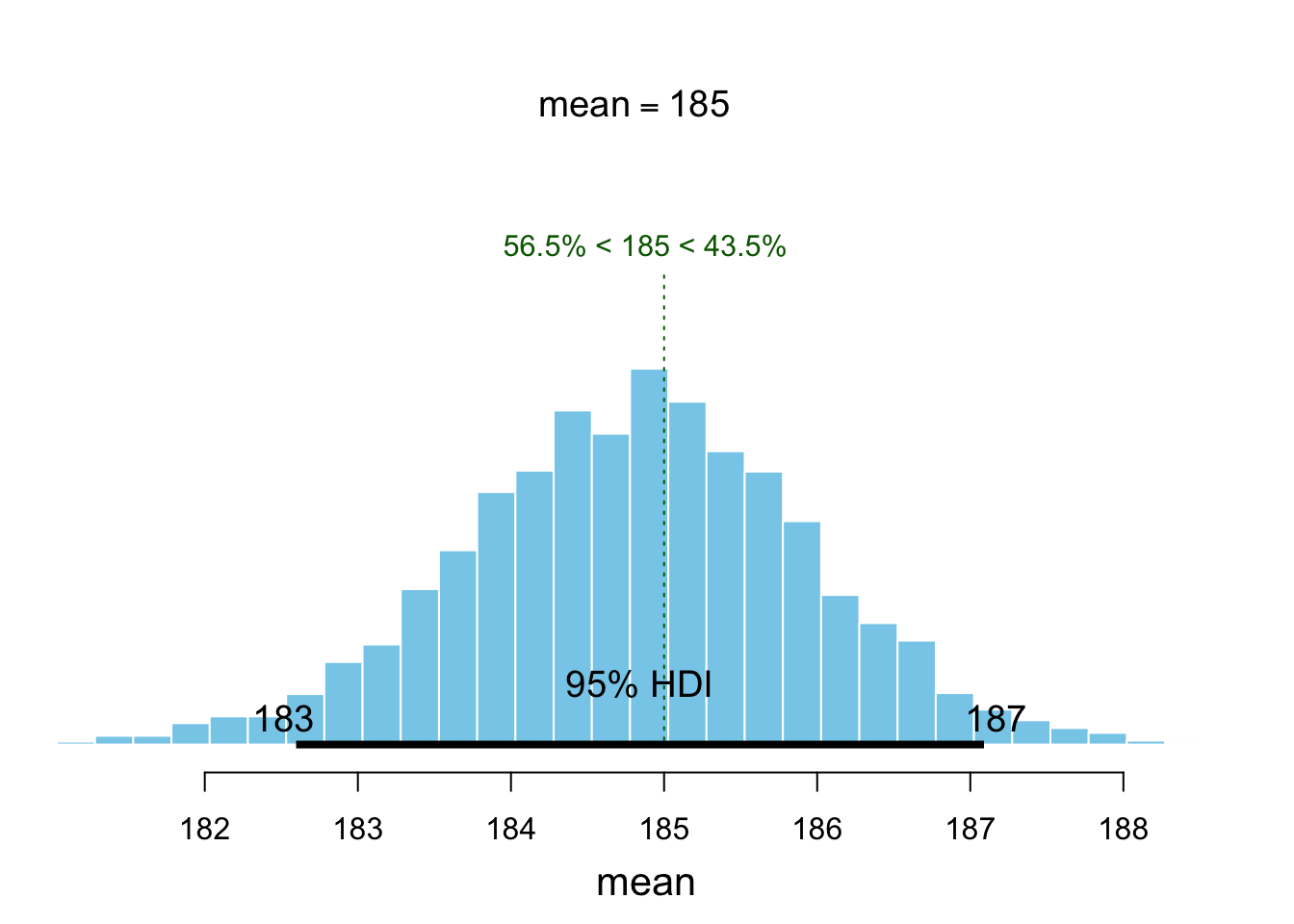

Joonis 12.2: Bayesi bootstrapi posteerior USA presidentide keskmisele pikkusele.

HPDI(heights_bb$V1, prob = 0.95)
#> |0.95 0.95| 
#>   183   187

Vaikimisi pannakse bayesboot() funktsioonis statistiku arvutamisel kaalud (prior) valimi indeksile, mis annab erineva tulemuse kui näiteks kaalutud keskmise arvutamisel, kus kaalud (prior) pannakse valimi väärtustele.

Aritmeetilise keskmise Bayesi bootstrap väärtused kasutades kaalutud keskmise funktsiooni weighted.mean saab niimoodi:

heights_bb_w <- bayesboot(heights$value, 
                         weighted.mean, 
                         use.weights = TRUE)

Tõenäosus, et keskmine on suurem kui 182 cm

mean(heights_bb[, 1] > 182)
#> [1] 0.989

Kahe keskväärtuse erinevus (ES = keskmine1 - keskmine2):

set.seed(1)
## Simulate two random normal distributions with mean 0. 
## True difference is 0.
dfr <- tibble(a = rnorm(10, 0, 1), 
              b = rnorm(10, 0, 1),
              c = a - b)
dfr_bb <- bayesboot(dfr$c, weighted.mean, use.weights = TRUE )
plot(dfr_bb, compVal = 0)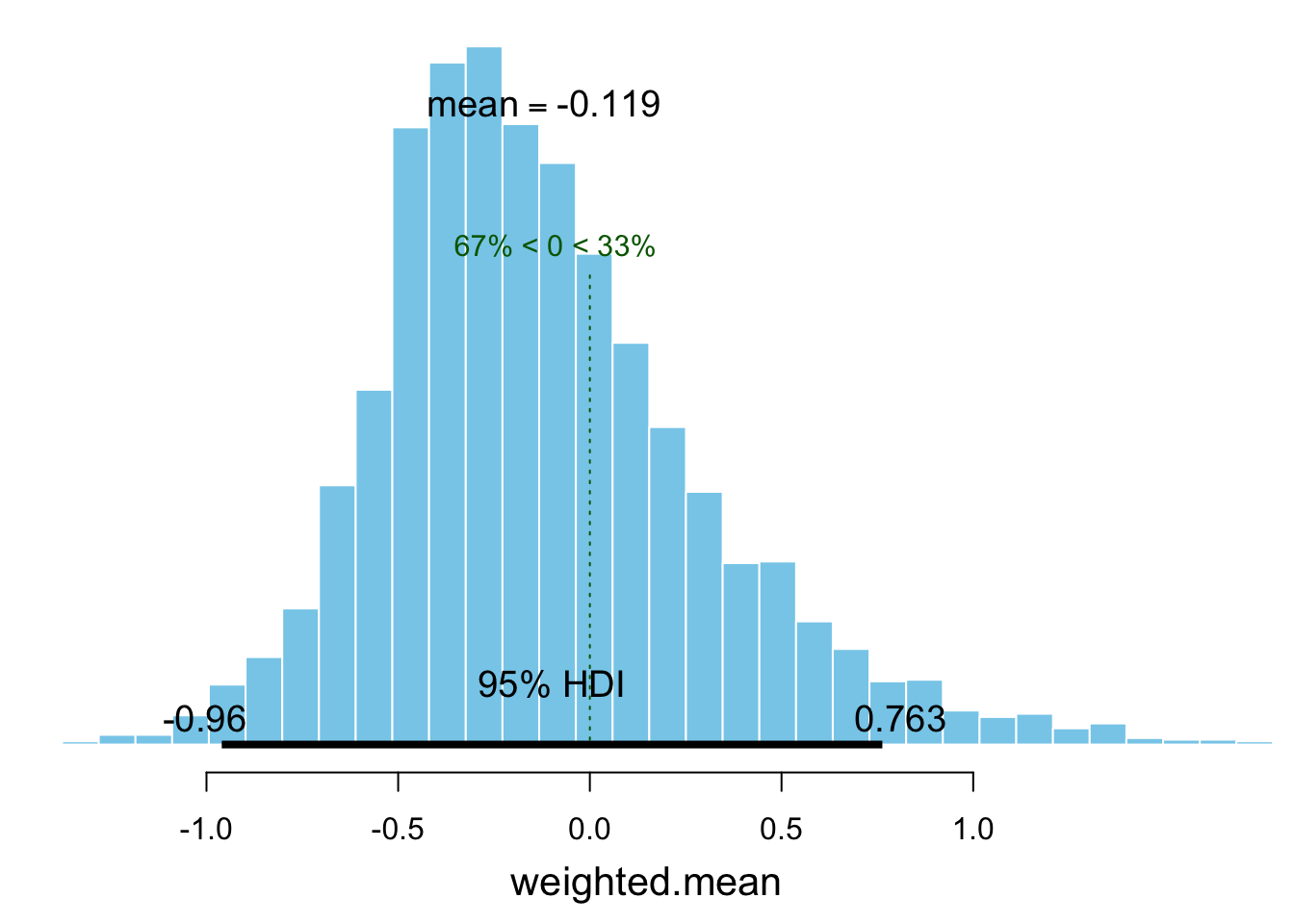

Joonis 12.3: Bayesi bootstrap ES-le.

BayesianFirstAid raamatukogu funktsioon bayes.t.test() annab kasutades t-jaotuse tõepäramudelit üsna täpselt sama vastuse. See raamatukogu eeldab JAGS mcmc sämpleri installeerimist. Abi saab siit https://github.com/rasmusab/bayesian_first_aid ja siit https://faculty.washington.edu/jmiyamot/p548/installing.jags.pdf.

Parameetriline bootstrap

Kui me arvame, et me teame, mis jaotusega on meie andmed, ja meil on suhteliselt vähe andmepunkte, võib olla mõistlik lisada bootstrapile andmete jaotuse mudel. Näiteks, meie USA presidentide pikkused võiksid olla umbkaudu normaaljaotusega (sest me teame, et USA meeste pikkused on seda). Seega fitime kõigepealt presidentide pikkusandmetega normaaljaotuse ja seejärel tõmbame bootsrap valimid sellest normaaljaotuse mudelist. Normaaljaotuse mudelil on 2 parameetrit: keskmine (mu) ja standardhälve (sigma), mida saame fittida valimiandmete põhjal:

mu <- mean(heights$value)
sigma <- sd(heights$value)
N <- length(heights$value)
sample_means <- tibble(value = rnorm(N * 1000, mu, sigma), 
                       indeks = rep(1:1000, each = N))

sample_means_sum <- sample_means %>% 
  group_by(indeks) %>% 
  summarise(Mean = mean(value))

ggplot(sample_means_sum, aes(x = Mean)) +
  geom_histogram(color = "white", bins = 20)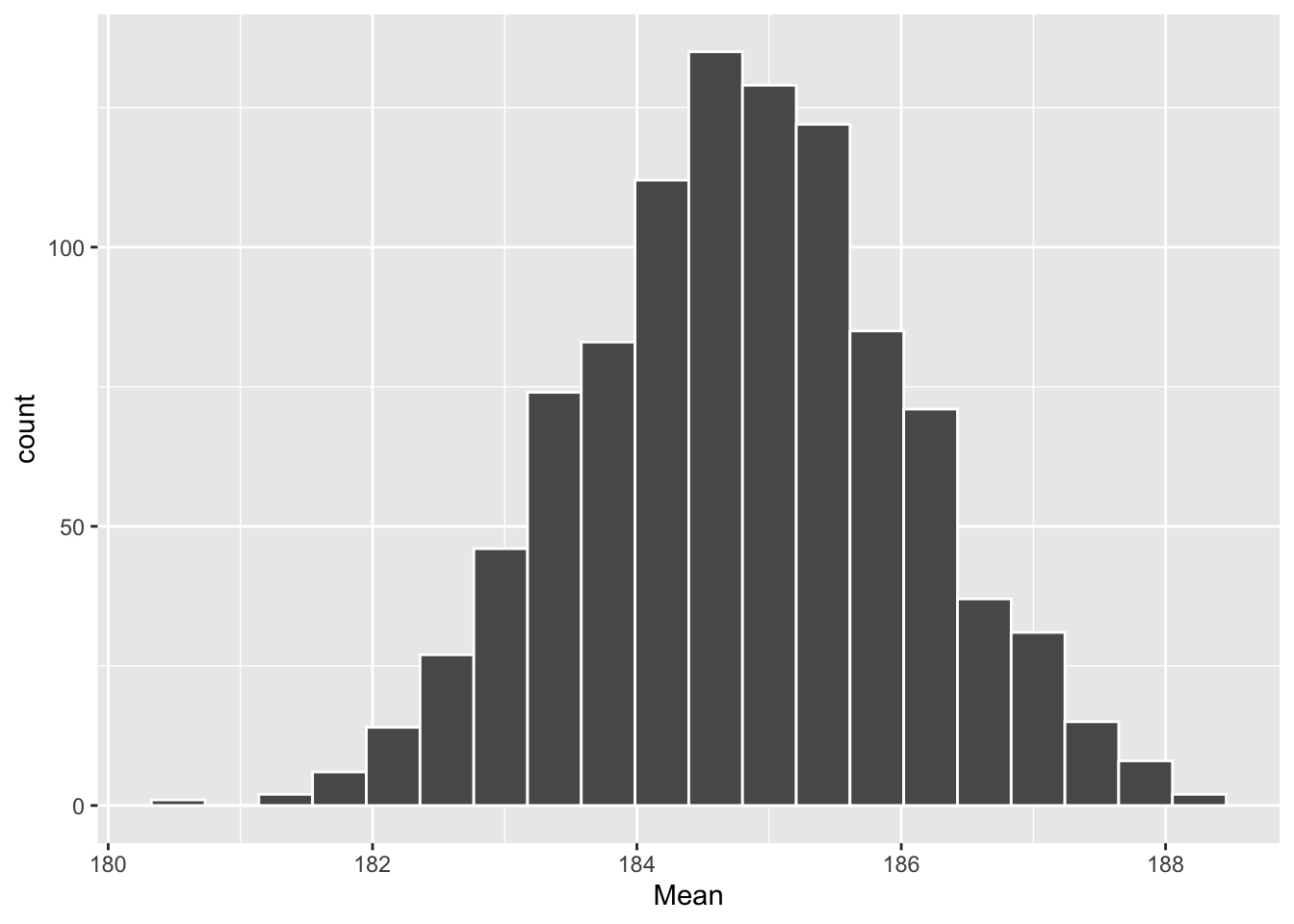

Joonis 12.4: Parameetrilise bootstrapi posteerior USA presidentide keskmisele pikkusele.

HPDI(sample_means_sum$Mean)
#> |0.89 0.89| 
#>   183   187

Üldiselt ei soovita me parameetrilist bootstrappi väga soojalt, sest täisbayesiaanlik alternatiiv, mida me kohe õppima asume, on sellest paindlikum.

Joonis 12.5: Bootstrappimise meetodid.

Bootstrappimine ei ole kogu tõde

Bootstrappimine on võimas ja väga laia kasutusalaga meetodite kogum. Sellel on siiski üks oluline puudus. Nimelt arvestab bootstrap ainult andmetega ja ignoreerib taustateadmisi (parameetriline bootstrap küll eeldab taustateadmisetele tuginevalt jaotusmudelit, kuid ignoreerib kogu muud taustateadmist). Miks on see probleem?

Mõtleme hetkeks sellele teadusliku meetodi osale, millel põhineb suuresti näiteks Darwini liikide tekkimise argument. See on nn inference to the best explanation, mille kohaselt on eelistatud see teooria, mis on parimas kooskõlas faktidega, ehk mille kehtimise korral on meie andmete esinemine kõige tõenäolisem. Kui mõni hüpotees omistab andmete esinemisele suure tõenäosuse, siis me ütleme tehnilises keeles, et see hüpotees on tõepärane (has high likelihood). Esmapilgul tundub see kõik igati mõistlik, kuid proovime lihtsat mõtteeksperimenti. Selles juhtub nii, et loteriil võidab peaauhinna meile tundmatu kodanik Franz K. Meil on selle fakti (ehk nende andmete) seletamiseks kaks teooriat: 1. Franz K. võit oli juhuslik (loterii oli aus ja keegi peab ju võitma) ja 2. Franz K. noorem õde võltsis loterii tulemusi oma venna kasuks. Teine teooria sobib andmetega palju paremini kui esimene (sest kuigi keegi peab võitma, Franz K. võiduvõimalus oli väga väike); aga ometi eelistab enamus mõistlikke inimesi esimest teooriat. Põhjus on selles, et meil pole iseenesest mingit alust arvata, et Franz K.-l üldse on noorem õde, või et see õde omaks ligipääsu loteriile. Kui me aga saame teada, et Franz K. noorem õde tõesti korraldab loteriid, siis leiame kohe, et asi on kahtlane.

Siit näeme, et lisaks tõepärale on selleks, et me usuksime mõne teooria kehtimisse, vaja veel, et see teooria oleks piisavalt tõenäoline meie taustateadmiste valguses. Bayesi teoreem ei tee muud, kui arvutab teooria kehtimise posterioorse tõenäosuse (järeltõenäosuse), kasutades selleks meie eelteadmiste ja tõepära kvantitatiivseid mudeleid. Seega, Bayesi paradigmas ei arvesta me mitte ainult andmetega, vaid ka taustateadmistega, sünteesides need kokku üheks posterioorseks jaotuseks ehk järeljaotuseks. Selle jaotuse arvutamine erineb bootstrapist, kuid tema tõlgendus ja praktiline töö sellega on sarnane. Erinevalt tavapärasest bootstrapist on Bayes parameetriline meetod, mis sõltub andmete modelleerimisest modeleerija poolt ette antud jaotustesse (normaaljaotus, t jaotus jne). Tegelikult peame me Bayesi arvutuseks modelleerima vähemalt kaks erinevat jaotust: andmete jaotus, mida me kutsume likelihoodiks ehk tõepäraks, ning eelneva teadmise mudel ehk prior, mida samuti modeleeritakse tõenäosusjaotusena.

Bootstrapil on mõned imelikud formaalsed eeldused: 1. väärtused, mis ei esine valimiandmetes, on võimatud, 2. Väärtused, mis esinevad väljaspool valimi väärtuste vahemikku, on võimatud, 3. andmetes ei esine ajasõltuvusi ega hierarhilisi struktuure. Nendest puudustest hoolimata kasutatakse bootstrappimist laialt ja edukalt — eelkõige tema lihtsuse ja paindlikuse tõttu. Küll aga tähendab see, et bootstrap on harva parim võimalik meetod mingi ülesande lahendamiseks.

Ehkki bootstrappimine ei arvesta taustateadmistega, ei tee seda olulisel määral ka paljud Bayesi mudelid (mudeldaja vaba valiku tõttu, mitte selle pärast, et mudel ei suudaks taustainfot inkorporeerida). Bayesi meetodite väljatöötajad ei tea sageli ette, milliste teaduslike probleemide lahendamiseks nende mudeleid hakatakse kasutama, ja seega ei kirjuta nad mudelisse ka väga ranget eelteadmist. Nende mudelite teadlastest kasutajad lepivad sageli selllega ja lasevad oma mudelite kaudu “andmetel kõneleda” enam-vähem sellistena, nagu need juhtuvad olema. Sellist lähenemist ei saa alati hukka mõista, sest vahest ei olegi meil palju eelteadmisi oma probleemi kohta, küll aga tuleb mainida, et sellistel juhtudel annab bootstrappimine sageli lihtsama vaevaga väga sarnase tulemuse kui Bayesi täismäng.