1 Sissejuhatus: maailm, teooria ja mudel

Suur ja väike maailm

Kuna maailmas on kõik kõigega seotud, on seda raske otse uurida. Teadus töötab tänu sellele, et teadlased lõikavad reaalsuse väikesteks tükkideks, kasutades tordilabidana teaduslike hüpoteese, ning uurivad seda tükikaupa lootuses, et kui kõik tükid on korralikult läbi nätsutatud, saab sellest taas tordi kokku panna. Tüüpiline bioloogiline hüpotees pakub välja tavakeelse (mitte matemaatilise) seletuse mõnele piiritletud loodusnähtusele.

Näiteks antibiootikume uuritakse keemilise sideme tasemel kasutades orgaanilise keemia meetodeid. Antibiootikumide molekulaarseid märklaudu uuritakse molekulaarbioloogiliste meetoditega, nende toimet uuritakse rakubioloogia ja füsioloogia meetoditega, aga kaasajal on väga olulised ka ökoloogilised, evolutsioonilised, meditsiinilised, põllumajanduslikud, majanduslikud ja psühholoogilised aspektid. Kõigil neil tasanditel on loodud palju hüpoteese, millest kokku moodustub meie teadmine antibiootikumide kohta. Neid väga erinevaid asju, mida me kutsume hüpoteesideks saab sageli jagada osadeks (ja neid osa-hüpoteese omakorda osadeks), mida saab omakorda osaliselt kirjeldada matemaatiliste formalismide ehk mudelite abil. Ja neid mudeleid saab võrrelda andmetega. Kuigi erinevate tasemete hüpoteesid on tavakeeles üksteisest väga erinevad, on neid kirjeldavad mudelid sageli matemaatiliselt sarnased.

Kui mudel on teooria lihtsustus, siis teooria on maailma lihtsustus.

Mudeliteks nimetatakse bioloogias väga erinevaid asju: skeeme, diagramme, füüsikalisi mudeleid (näit Watsoni ja Cricki poolt kasutatud nukleotiidimudelid), mudelorganisme, katsesüsteeme, matemaatilisi mudeleid jms. Üldiselt teeb mudeli mudeliks, et see asendab selle, mida teadlane tegelikult uurida tahab millegagi, mida on lihtsam mõista, manipuleerida või uurida. Meie räägime edaspidi ainult matemaatilisest mudelist ja eriti selle erijuhust, statistilisest ehk stohhastilisest mudelist.

Mis juhtub, kui teie mudel, ja seega ka hüpotees, mis selle mudeli genereeris, on andmetega kooskõlas? Kas see tähendab, et see hüpotees vastab tõele? Või, et see on tõenäoliselt tõene? Kahjuks on vastus mõlemale küsimusele eitav. Põhjuseks on asjaolu, et enamasti leiab iga nähtuse seletamiseks rohkem kui ühe alternatiivse teadusliku hüpoteesi ning rohkem kui üks üksteist välistav hüpotees võib olla olemasolevate andmetega võrdses kooskõlas. Asja teeb veelgi hullemaks, et teoreetiliselt on võimalik sõnastada lõpmata palju erinevaid teooriaid, mis kõik pakuvad alternatiivseid ja üksteist välistavaid seletusi samale nähtusele. Kuna hüpoteese on lõpmatu hulk, aga andmete hulk on alalti lõplik, siis saab igas teaduslikus faktis kahelda.
Ei saa kindel olla, et parimad teooriad on meile üldse kunagi pähe torganud ning, et meie poolt kogutud vähesed andmed kajastavad hästi tegelikkust.

Ca. 1910 mõtlesid Bertrand Russell ja G.E. Moore välja tõe vastavusteooria, mille kohaselt tõest lausungit eristab väärast vastavus füüsikalisele maailmale. Seega on tõesed ainult need laused, mis vastavad asjadele. Ehkki keegi ei oska siiani öelda, mida vastavus selles kontekstis tähendab või kuidas seda saavutada, on vastavusteooria senini kõige populaarsem tõeteooria filosoofide hulgas (mis on kõnekas alternatiivide kohta). Samamoodi, kui lausete vastavusest maailmaga, võime rääkida ka võrrandite (ehk mudelite) vastavusest lausetega. Vastavusest lausetaga sellepärast, et mudelid on loodud kirjeldama teaduslikke teooriaid, mitte otse maailma. Seega ei pea me muretsema mudelite tõeväärtuse pärast. Võib isegi väita, et mudeli tõeväärtusest rääkimine on kohatu.

1. Näide: politoloogia.

Meil on hüpotees (H1), mille kohaselt demokraatlikus süsteemis käituvad valijad ratsionaalselt ehk lähtuvalt endi huvidest (Achen and Bartels 2016). Alternatiiv (H2) ütleb, et valijad ei vali poliitikuid lähtuvalt oma tegelikest huvidest. Kuna H1 on liiga lai, et seda otse andmetega võrrelda, tuletame sellest kitsama alamhüpoteesi (H1.1), mille kohaselt valijad eelistavad tagasi valida kandidaate, kes on ennast tõestanud sellega, et saavad hakkama majanduse edendamisega. Seega, poliitikud, kes on võimekad majanduse vallas, valitakse tagasi suurema tõenäosusega kui need, kes seda ei ole. Sellest hüpoteesist tuletati kaks andemete vastu testitavat järelmit: - H1.1.1 – majandusel läheb keskeltläbi paremini juba tagasi valitud poliitikute all kui esimest korda valitud poliitkute all, kelle ridu ei ole veel elektoraadi poolt harvendatud ja - H1.1.2 – majandusnäitajate varieeruvus on esimesel juhul väiksem, sest kehvemad poliitikud on juba valimist eemaldatud. Esimese järelmi testimiseks kasutati statistilise mudelina (m1) aritmeetilist keskmist koos standardveaga ja teise järelmi jaoks (m2) standardhälvet.

Tulemused olid paraku vastupidised H1.1.1 ja H1.1.2 poolt ennustatuga, millest autorid tegid järelduse, et olemasolevad andmed ei toeta hüpoteesi H1.1 (andmete vähesuse tõttu nad ei arvanud, et nad oleksid H1.1-e ümber lükanud). Seega, andmed fititi mudelitesse m1 ja m2, nende fittide põhjal tehti järeldused H1.1.1 ja H1.1.2 kohta (et m1 ja H1.1.1 ning m2 ja H1.1.2 vahel puudub kooskõla), mille põhjal omakorda tehti järeldus H1.1 kohta (et H1.1-e ei õnnestunud kinnitada), mille põhjal üksi ei tehtud formaalset järeldust H1 kohta. H1 vs. H2 kohta tehakse järeldus alles raamatu lõpus, lähtudes H1.1, H1.2, …, H1.n kohta tehtud järeldustest.

2. Näide: populatsioonigeneetika.

Populatsioonigeneetikas on evolutsioon defineeritud kui alleelide sageduste muutumine põlvkonnast põlvkonda. Kõigepealt defineeriti tingimused, milliste kehtimisel alleelide sagedus EI muutu. Need on juhuslik sigimine populatsioonis, lõpmata suur populatsioon, mis koosneb diploidsetest organismidest, kellel on 1 geneetiline lookus ja 2 alleeli. See on Hardy-Weinbergi printsiip, millel põhineb enamus klassikalisest populatsioonigeneetikast ja mida kirjeldab võrrand

\[p^2 + 2pq + q^2 = 1\]

kus \(p^2\), \(2pq\) ja \(q^2\) on genotüüpide \(AA\), \(Aa\) ja \(aa\) sagedused sugurakkudes ning \(p\) ja \(q\) on alleelide \(A\) ja \(a\) sagedused (ning \(p + q = 1\)). Populatsioonis, mis on Hardy-Weinbergi tasakaalus, on \(p\) ja \(q\) põlvkondade vältel muutumatud. Selleks, et tasakaalu lõhkuda, toome mudelisse lisaparameetri \(w\), mis iseloomustab valikusurvet ehk kohasust (fitnessi). Kohasus iseloomustab looduliku valiku poolt tingitud genotüüpide sageduste muutust populatsioonis. Nüüd saame deterministliku mudeli (deterministliku, sest mudeli parameetritele kindlad väärtused omistades ja mudeli läbi arvutades saame vastuseks sama arvu, ükskõik mitu korda me seda arvutust ka ei kordaks):

\[p^2wAA + 2pqwAa + q^2waa = w_{mean}\]

kus \(w_{mean}\) on populatsiooni keskmine kohasus, \(wAA\) on genotüübi \(AA\) kohasus jne. Kui me teame parameetrite \(p, q, wAA, wAa\) ja \(waa\) väärtusi, saame hõlpsasti arvutada populatsiooni kohasuse.

Vaadates maailma mudeli pilgu läbi, juhul kui looduses mõõdetud genotüüpide sageduse muutus erineb mudelist arvutatud \(w_{mean}\)-ist, siis on meil tegemist geneetilise triiviga. Geneetiline triiv on genotüübisageduste juhuslik muutus populatsioonis, mis on seda suurem, mida väiksem on populatsioon ja mida väiksem on valikusurve populatsioonile. Seega oleks nagu võimalik geneetilise triivi olemasolu tuvastada alati, kui empiiriline genotüübisageduste muutuse kiirus erineb mudeli punktennustusest \(w_{mean}\). Selle deterministliku mudeli järgi on valik ja triiv teineteist välistavad: kui empiiriline kohasus = \(w_{mean}\), siis valik; muidu triiv.

Samas, kui me eeldame, et populatsiooni suurus ei ole lõpmata suur, tuleb mudelisse sisse juhuslik valimiviga. Mida väiksem on populatsioon, seda suurema tõenäosusega ei anna juhuslik paljunemine ka ilma valikusurveta populatsioonis järgmist põlvkonda, mille genotüübisagedused vastaksid eelmise põlvkonna genotüübisagedustele (ptk xxx simuleerime me juhuslikku valimiviga normaaljaotuse mudelist). Seega muutub meie deterministlik mudel stohhastiliseks mudeliks, mille väljund ei ole enam punktväärtus \(w_{mean}\)-le vaid rida tõenäosusi erinevatele \(w_{mean}\)-i väärtustele (sellise mudeli kuju vt ptk xxx). Selle mudeli järgi ei ole valik ja triiv enam erinevat tüüpi protsessid, vaid ühe kontiinumi kaks poolust; kontiinumi, mis sõltub populatsiooni suurusest ja valikusurve tugevusest. Kuna puhas looduslik valik saab mudeli järgi toimuda ainult lõpmata suures populatsioonis, milliseid looduses ei leidu, siis on alleeli \(a\) sageduse muutus teadlase poolt uuritavas looduslikus populatsioonis x ühtaegu nii loodusliku valiku kui geenitriivi tagajärg.

Mis juhtub, kui me ei tee mudeli struktuurist otse järeldusi maailma kohta? Nüüd alustame me eeldusest, et looduslik valik on looduses reaalselt toimuv protsess. Näiteks Darwin nägi valikut loodusliku põhjusliku protsessina, mis on samas stohhastiline (mitte kõik kõrgema kohasusega organismid ei anna järglasi). Selle vaate kohaselt on loodusliku valiku tagajärjeks kallutatud valim genotüüpidest, mille avaldumise poolt põhjustatud erinevused organismides viisid nende erinevale paljunemisedukusele. Seega on valik ja triiv erinevat tüüpi looduslikud protsessid, mitte mudeli väljundid. Niisiis teeme rangelt vahet valikul ja triivil nende põhjuste järgi. Kui tõuseb kasulike genotüüpidega organismide osakaal, siis on tegemist loodusliku valiku poolt tingitud evolutsiooniga. Kui aga genotüüpide sageduste muutumine ei ole põhjustatud indiviidide füüsilistest erinevustest, siis on tegu geneetilise triivi poolt tingitud evolutsiooniga.

Nõnda saame evolutsiooniteooriast lähtudes hoopis teistsuguse vaate bioloogiale, kui mudeleid otse tõlgendades. Muidugi ei tähenda see, et me ei vaja mudeleid. Vajame küll, aga me peame neid ettevaatlikult tõlgendama, pidades silmas oma teooriate sisu. Andemetega fititud mudelit tõlgendame teooria kaudu ja seda ei tohiks kunagi teha otse mudelist päris maailmale.

Mudeli väike maailm

Ülalmainitud teadusliku meetodi puudused tingivad, et meie huvides on oma teaduslikke probleeme veel ühe taseme võrra lihtsustada, taandades need statistilisteks probleemideks. Selleks tuletame tavakeelsest teaduslikust teooriast täpselt formuleeritud matemaatilise mudeli ning seejärel asume uurima oma mudelit lootuses, et mudeli kooskõla andmetega ütleb meile midagi teadusliku hüpoteesi kohta. Enamasti töötab selline lähenemine siis, kui mudeli ehitamisel arvestati võimaliku andmeid genereeriva mehhanismiga – ehk, kui mudeli matemaatiline struktuur koostati teaduslikku hüpoteesi silmas pidades. Mudelid, mis ehitatakse silmas pidades puhtalt matemaatilist sobivust andmetega, ei kipu omama teaduslikku seletusjõudu, kuigi neil võib olla väga hea ennustusjõud.

Meil on kaks hüpoteesi, A ja B. Juhul kui A on tõene ja B on väär, kas on võimalik, et B on tõele lähemal kui A? Kui A ja B on teineteist välistavad punkthüpoteesid parameetri väärtuse kohta, siis on vastus eitav. Aga mis juhtub, kui A ja B on statistilised mudelid? Näiteks, kui tõde on, et eesti meeste keskmine pikkus on 178.3 cm ja A ütleb, et keskmine pikkus jääb kuhugi 150 cm ja 220 cm vahele ning B ütleb, et see jääb kuhugi 179 cm ja 182 cm vahele, siis on B “tõele lähemal” selles mõttes, et meil on temast teaduslikus mõttes rohkem kasu. Siit on näha oluline erinevus teadusliku hüpoteesi ja statistilise mudeli vahel: hüpotees on orienteeritud tõele, samal ajal kui mudel on orienteeritud kasule.

Mudeli maailm erineb päris maailmast selle poolest, et mudeli maailmas on kõik sündmused, mis põhimõtteliselt võivad juhtuda, juba ette teada ja üles loendatud (seda sündmuste kogu kutsutakse parameetriruumiks). Tehniliselt on mudeli maailmas üllatused võimatud.

Lisaks, tõenäosusteooriat, ja eriti Bayesi teoreemi, kasutades on meil garantii, et me suudame mudelis leiduva informatsiooniga ümber käia parimal võimalikul viisil. Kõik see rõõm jääb siiski mudeli piiridesse. Mudeli eeliseks teooria ees on, et hästi konstrueeritud mudel on lihtsamini mõistetav — erinevalt vähegi keerulisemast teaduslikust hüpoteesist on mudeli eeldused ja ennustused läbinähtavad ja täpselt formuleeritavad. Mudeli puuduseks on aga, et erinevalt teooriast ei ole mingit võimalust, et mudel vastaks tegelikkusele. Seda sellepärast, et mudel on taotluslikult lihtsustav (erandiks on puhtalt ennustuslikud mudelid, mis on aga enamasti läbinähtamatu struktuuriga). Mudel on kas kasulik või kasutu; teooria on kas tõene või väär. Mudeli ja maailma vahel võib olla kaudne peegeldus, aga mitte kunagi otsene side. Seega, ükski number, mis arvutatakse mudeli raames, ei kandu sama numbrina üle teaduslikku ega päris maailma. Ja kogu statistika (ka mitteparameetriline) toimub mudeli väikses maailmas. Arvud, mida statistika teile pakub, elavad mudeli maailmas; samas kui teie teaduslik huvi on suunatud päris maailmale. Näiteks 95% usaldusintervall ei tähenda, et te peaksite olema 95% kindel, et tõde asub selles intervallis – sageli ei tohiks te seda nii julgelt tõlgendada isegi kitsas mudeli maailmas.

3. Näide: Aristoteles, Ptolemaios ja Kopernikus

Aristoteles (384–322 BC) lõi teooria maailma toimimise kohta, mis domineeris haritud eurooplase maailmapilti enam kui 1200 aasta vältel. Tema ühendteooria põhines maailmapildil, mis oli üldtunnustatud juba sajandeid enne Aristotelest ja järgneva 1500 aasta jooksul kahtlesid selles vähesed mõistlikud inimesed. Selle kohaselt asub universumi keskpunktis statsionaarne maakera ning kõik, mida siin leida võib, on tehtud neljast elemendist: maa, vesi, õhk ja tuli. Samas, kogu maailmaruum alates kuu sfäärist on tehtud viiendast elemendist (eeter), mida aga ei leidu maal (nagu nelja elementi ei leidu kuu peal ja sealt edasi). Taevakehad (kuu, päike, planeedid ja kinnistähed) tiirlevad ümber maa kontsentrilistes sfäärides, mille vahel pole vaba ruumi. Seega on kogu liikumine eetri sfäärides ühtlane ja ringikujuline ja see liikumine põhjustab pika põhjus-tagajärg ahela kaudu kõiki liikumisi, mida maapeal kohtame. Kaasa arvatud sündimine, elukäik ja surm. Kõik, mis maapeal huvitavat, ehk kogu liikumine, on algselt põhjustatud esimese liikumise poolt, mille käivitab kõige välimises sfääris paiknev meie jaoks mõistetamatu intellektiga “olend”.

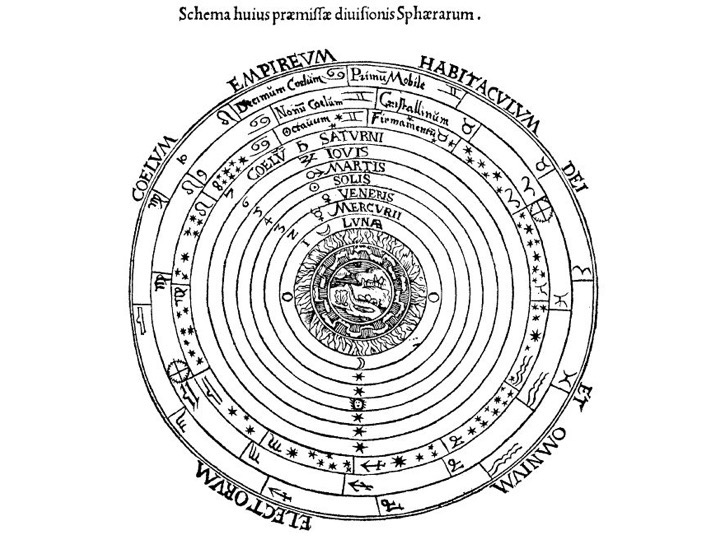
Joonis 1.1: Keskaegne aristotellik maailm.

Aristotelese suur teooria ühendab kogu maailmapildi alates meie mõistes keemiast ja kosmoloogiast kuni bioloogia, maateaduse ja isegi geograafiani. Sellist ühendteooriat on erakordselt raske ümber lükata, sest seal on kõik kõigega seotud.

Aristarchus (c. 310 – c. 230 BC) proovis seda siiski, väites, et tegelikult tiirleb maakera ümber statsionaarse päikese. Ta uskus ka, et kinnistähed on teised päikesed, et universum on palju suurem kui arvati (ehkki kaasaegne seisukoht oli, et universumi mastaabis ei ole maakera suurem kui liivatera) ning, et maakera pöörleb ümber oma telje. Paraku ei suutnud Aristarchuse geotsentriline teooria toetajaid leida, kuna see ei pidanud vastu vaatluslikule testile. Geotsentrilisest teooriast tuleneb nimelt loogilise paratamatusena, et tähtedel esineb maalt vaadates parallaks. See tähendab, et kui maakera koos astronoomiga teeb poolringi ümber päikese, siis kinnistähe näiv asukoht taevavõlvil muutub, sest astronoom vaatleb teda teise nurga alt. Pange oma nimetissõrm näost u 10 cm kaugusele, sulgege parem silm, seejärel avage see ning sulgege vasak silm ja te näete oma sõrme parallaksi selle näiva asukoha muutusena. Mõõtmised ei näidanud aga parallaksi olemasolu (sest maa trajektoori diameeter on palju lühem maa kaugusest tähtedest). Parallaksi suudeti esimest korda mõõta alles 1838, siis kui juba iga koolijüts uskus, et maakera tiirleb ümber päikese!

Ühte Aristotelese kosmoloogia olulist puudust nähti siiski kohe. Nimelt ei suuda Aristoteles seletada, miks osad planeedid teavavõlvil vahest suunda muudavad ja mõnda aega lausa vastupidises suunas liiguvad (retrogressioon). Kuna astronoomiat kasutasid põhiliselt astroloogid, siis pöörati planeetide liikumisele suurt tähelepanu. Lahenduseks ei olnud aga mitte suure teooria ümbertegemine või ümberlükkamine, vaid uue teaduse nõudmine, mis “päästaks fenomenid”. Siin tuli appi Ptolemaios (c. AD 100 – c. 170), kes lõi matemaatilise mudeli, kus planeedid mitte lihtsalt ei liigu ringtrajektoori mõõda, vaid samal ajal teevad ka väiksemaid ringe ümber esimese suure ringjoone. Neid väiksemaid ringe kutsutakse epitsükliteks. See mudel suutis planeetide liikumist taevavõlvil piisavalt hästi ennustada, et astroloogide seltskond maha rahustada.

Ptolemaiosel ja tema järgijatel oli tegelikult mitu erinevat mudelit. Osad neist ei sisaldanud epitsükleid ja maakera ei asunud tema mudelites universumi keskel, vaid oli sellest punktist eemale nihutatud — nii et päike ei teinud ringe ümber maakera vaid ümber tühja punkti. Kuna leidus epitsüklitega mudel ja ilma epitsükliteta mudel, mis andsid identseid ennustusi, on selge, et Aristotelese teooria ja fenomenide päästmise mudelid on põhimõtteliselt erinevad asjad. Samal ajal, kui Aritoteles seletas maailma põhiolemust põhjuslike seoste jadana (mitte matemaatiliselt), kirjeldas/ennustas Ptolemaios sellesama maailma käitumist matemaatiliste (mitte põhjuslike) struktuuride abil.

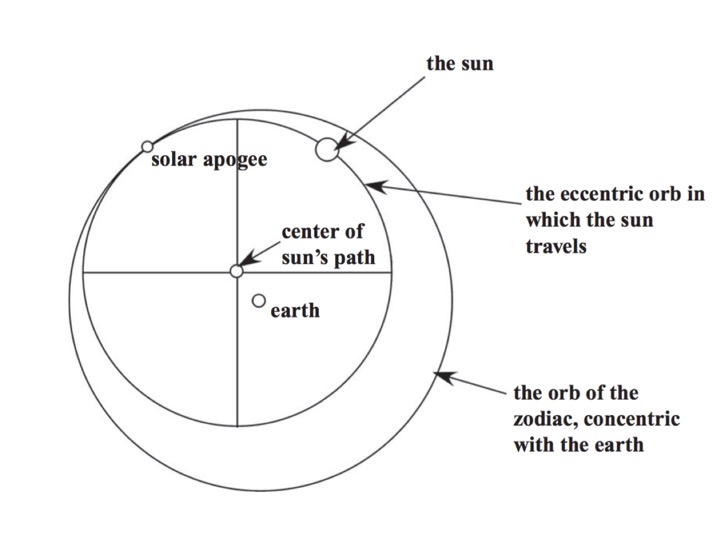
Joonis 1.2: Ilma epitsükliteta ptolemailine mudel.

Nii tekkis olukord, kus maailma mõistmiseks kasutati Aristotelese ühendteooriat, aga selle kirjeldamiseks ja tuleviku ennustamiseks hoopis ptolemailisi mudeleid, mida keegi päriselt tõeks ei pidanud ja mida hinnati selle järgi, kui hästi need “päästsid fenomene”.

See toob meid Kopernikuse (1473 – 1543) juurde, kes teadusajaloolaste arvates vallandas 17. sajandi teadusliku revolutsiooni, avaldades raamatu, kus ta asetab päikese universumi keskele ja paneb maa selle ümber ringtrajektooril tiirlema. Kas Kopernikus tõrjus sellega kõrvale Aristotelese, Ptolemaiose või mõlemad? Tundub, et ta soovis kolmandat, suutis esimest ning tolleaegsete lugejate arvates üritas teha teist — ehk välja pakkuda alternatiivi ptolemailistele mudelitele, mis selleks ajaks olid muutunud väga keerukaks (aga ka samavõrra ennustustäpseks). Kuna Kopernikuse raamat läks trükki ajal, mil selle autor oli juba oma surivoodil, kirjutas sellele eessõna üks tema vaimulikust sõber, kes püüdis oodatavat kiriklikku pahameelt leevendada vihjates, et päikese keskele viimine on vaid mudeldamise trikk, millest ei tasu järeldada, et maakera ka tegelikult ümber päikese tiirleb (piibel räägib, kuidas jumal peatas taevavõlvil päikese, mitte maa). Ja kuna eessõna oli anonüümne, eeldasid lugejad, et selle kirjutas autor. Lisaks, kuigi Kopernikus tõstis päikese keskele, jäi ta planeetide ringikujuliste trajektooride juurde, mis tähendab, et selleks, et tema teooria fenomenide päästmisel hätta ei jääks, oli ta sunnitud maad ja planeete mõõda epitsükleid ümber päikese liigutama. Kokkuvõttes oli Kopernikuse mudel umbes sama keeruline kui ptolemailikud mudelid ja selle abil tehtud ennustused planeetide liikumise kohta olid väiksema täpsusega. Seega, ennustava mudelina ei olnud sel suuri eeliseid.

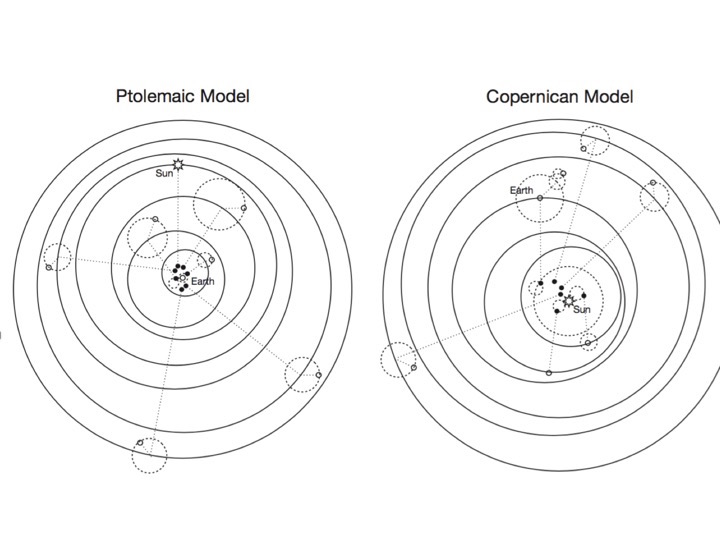
Joonis 1.3: Ptolemaiose ja Kopernikuse mudelid on üllatavalt sarnased.

Kopernikuse mudel suutis siiski ennustada mõningaid nähtusi (planeetide näiv heledus jõuab maksimumi nende lähimas asukohas maale), mida Ptolemaiose mudel ei ennustanud. See ei tähenda, et need fenomenid oleksid olnud vastuolus Ptolemaiose mudeliga. Lihtsalt, nende Ptolemaiose mudelisse sobitamiseks oli vaja osad mudeli parameetrid fikseerida nii-öelda suvalistele väärtustele. Seega Kopernikuse mudel töötas sellisel kujul, nagu see esitati, samas kui Ptolemaiose mudel vajas post hoc tuunimimst.

Kui vaadata Koperniku produkti teooriana, mitte mudelina, siis oli sellel küll selgeid eeliseid Aristotelese maailmateooria ees. Juba ammu oli nähtud komeete üle taevavõlvi lendamas (mis Aristotelese järgi asusid kinnistähtede muutumatus sfääris), nagu ka supernoova tekkimist ja kadu, ning enam ei olnud kaugel aeg, mil Galileo joonistas oma teleskoobist kraatreid kuu pinnal, näidates, et kuu ei saanud koosneda täiuslikust viiendast elemendist ja et sellel toimusid ilmselt sarnased füüsikalised protsessid kui maal. On usutav, et kui Kopernikus oleks jõudnud oma raamatule ise eessõna kirjutada, oleks tema teooria vastuvõtt olnud kiirem ja valulisem.