20 Mitmetasemelised mudelid

Mitmetasemeline mudel on regressioonimudel, kus andmed on struktureeritud gruppidesse ja mudeli koefitsiendid võivad erineda grupist gruppi.

Statistika teooria ütleb, et me peaksime oma mudelitesse hõlmama need faktorid, mida kasutati eksperimendi disainis. Mitmetasandilised mudelid on parim viis, kuidas mudelisse panna katsedisainis esinevaid erinevatel tasemetel klastreid ja samas vältida mudeli ülefittimist. Mitmetasandiline mudel kajastab sellise katse või vaatluse struktuuri, kus andmed ei grupeeru mitte ainult katse- ja kontrolltingimuste vahel, vaid ka lisaklastritesse ehk gruppidesse. Näiteks, kui me mõõdame platseebo-kontrollitud uuringus kümmet patsienti ja teeme igale patsiendile viis kordusmõõtmist (kahetasemeline mudel). Või kui meil on geeniuuring, kus uuritakse korraga 1000 valgu taset ja uuring toimub 10 laboris (3-tasemeline mudel). Või kui mõõdame kalamaksaõli mõju matemaatikaeksami tulemustele kümnes koolis, ja igas neist viies klassis (3-tasemeline mudel).

Tavapärane lähenemine oleks kõigepealt keskmistada andmed iga klassi sees ning seejärel keskmistada iga kooli sees (võtta igale koolile 5 klassi keskmine). Ning seejärel, võttes iga kooli keskmise üheks andmepunktiks, teha soovitud statistiline test (N = 10, sest meil on 10 kooli). Paraku, sellisel viisil talitades alahindame varieeruvust, mistõttu meie statistiline test alahindab ebakindluse määra arvutatud statistiku ümber. Hierarhilised mudelid, mis kajastavad adekvaatselt katse struktuuri, aitavad sellest murest üle saada. Üldine soovitus on, et kui teie katse struktuur seda võimaldab, siis peaksite alustama modelleerimist hierarhilistest mudelitest.

Mitmetasemelised mudelid on eriti kasulikud, kui teil on osades klastrites vähem andmepunkte kui teistes, sest nad vaatavad andmeid korraga nii klastrite vahel kui klastrite sees ning kannavad informatsiooni üle klastritest, kus on rohkem andmepunkte, nendesse klastritesse, kus on vähe andmeid. See tõstab hinnangute täpsust.

Tavapärane regressioonimudel on sageli vaadeldav mitmetasandilise mudeli erijuhuna. Näiteks kujutage ette mudelit, kus laste õppedukust on mõõdetud mitmes koolis. Kui gruppide (koolide) vaheline varieeruvus on väga madal, siis annab mitmetasemeline mudel sarnase tulemuse lihtsa mudeliga, kus kõik koolid on ühte patta kokku pandud. Ja vastupidi, kui koolid on üksteisest väga erinevad, siis võime sama hästi modelleerida iga kooli eraldi ja teistest sõltumatult. Samuti, kui meil on andmeid väga väheste koolide kohta, siis võib mitmetasandilsest mudelist saadav kasu olla tagasihoidlik, sest meil pole piisavalt andmeid, et modelleerida koolide vahelist varieeruvust. Samuti, kui meil on iga kooli kohta piisavalt palju andmeid, siis saame iga kooli eraldi modelleerides praktiliselt sama tulemuse kui mitmetasemelisest mudelist. Muudel juhtudel on tõenäoliselt mõistlikum modelleerida õppedukust kahetasemelises mudelis, korraga õpilase tasemel ja kooli tasemel.

20.1 kahetasemeline mudel algebra keeles

1. tase on õpilse tase, 2. tase on klassi tase. meil on j klassi, milles on erinev arv õpilasi. Iga õpilase kohta teame populaarsusindeksit (y - muutuja) ja sugu (x - muutuja). Klassi tasemel teame õpetaja staazi aastates (z - muutuja). Alustuseks on meil j regressioonivõrrandit, eraldi võrrand igale klassile

\[y_{ij} = b_{0j} + b_{1j}X_{ij} + e_{ij}\] (1. võrrand)

kus subskript j tähistab klassi ja i tähistab õpilast. Näit \(b_{1j}\) tähendab, et me fitime igale klassile oma \(b_1\) koefitsiendi (ja \(b_{0j}\), et fitime igale klassile oma \(b_0\)-i). Me eeldame, et igal klassil on erinevad \(b_0\) ja \(b_1\), mis tulevad vastavatest klassiülestest normaaljaotustest. Enamasti eeldame, et kõikide klasside varieeruvus on sama. Me modelleerime \(b_0\) ja \(b_1\) jaotusi, tuues sisse klassi tasemel muutuja z:

\[b_{0j} = \gamma_{00} + \gamma_{01} Z_j + u_{0j}\] (2. võrrand)

\[b_{1j} = \gamma_{10} + \gamma_{11} Z_j + u_{1j}\] (3. võrrand)

2. võrrand ennustab klassi keskmist populaarsusindeksit vastavalt õpetaja staazile.
3. võrrand ütleb, et populaarsuse ja soo seose tugevus sõltub õpetaja staazist – kui \(\gamma_{11} > 0\), siis on seos seda tugevam, mida staazikam on õpetaja. \(u_{0j}\) ja \(u_{1j}\) on residuaalide vead klassi tasemel, mille kohta me eeldame, et mean = 0 ja sõltumatust residuaalide vigadest õpilase tasemel (\(e_{ij}\)). \(u_{0j}\) residuaalide vigade dispersioon on \(\sigma^2_{u0}\) jne. \(u_{0j}\) ja \(u_{1j}\) covariance on \(\sigma^2_{u01}\) ja me ei eelda, et see = 0. Gamma koefitsiendid ei varieeru klasside vahel.

Asendades 1. võrrandis \(b_{0j}\) ja \(b_{1j}\), saame oma võrrandisüsteemi muuta üheks pikaks võrrandiks.

\[Y_{ij} = \gamma_{00} + \gamma_{10} X_{ij} + \gamma_{01} Z_j + \gamma_{11}X_{ij} Z_j + u_{1j} X_{ij} + u_{0j} + e_{ij}\]

Siis näeme uues võrrandis liiget \(\gamma_1 Z_j X_{ij}\), mis on interaktsiooniliige. Ilma interaktsioonita mudel näeb välja niimodi

\[Y_{ij} = \gamma_{00} + \gamma_{10} X_{ij} + \gamma_{01} Z_j + u_{1j} X_{ij} + u_{0j} + e_{ij}\]

juhusliku vealiige \(u_{ij}\) korrutub \(X_{ij}\)-ga, mistõttu sellest tulenev totaalne viga on erinev erinevatel \(X_{ij}\) väärtustel. Seega on meie mudel heteroskedastiline ja erineb selle poolest tavalistest lineaarsetest mudelitest, mis eeldavad homoskedastilisust e residuaalvea sõltumatust X-i väärtusest.

Teine oluline erinevus tavalisest lin mudelist on, et gupeeritud andmete puhul ei ole täidetud andmete iseseisvuse eeldus (gruppide sees modelleeritakse andmed korreleerituna - klassisisene korrelatsioon). Klassisisese korrelatsiooni saame intercept-only mudelist

\[Y_{ij} = \gamma_{00} + u_{0j} + e_{ij}\]

(selle mudeli saad, kui viskad pikast mudelist välja kõik X ja Z sisaldavad liikmed.) See mudel ajab varieeruvuse lahku kahe iseseisva komponendi vahel: \(\sigma^2_e\) (1. taseme vigade dispersioon \(e_{ij}\)) ja \(\sigma^2_{u0}\) (2. taseme vigade dispersioon \(u_{0j}\)).

Klassisisene korrelatsioon:

\[\rho = \frac{\sigma^2_{u0}}{\sigma^2_{u0} + \sigma^2_e}\]

rho annab grupistruktuuri poolt seletatud variace proportsiooni, mida võib tõlgendada kui kahe sama grupi juhusliku liikme vahelist oodatavat korrelatsiooni.

Üldiselt on kasulik töötada standardiseeritud regressioonikoefitsientidega, mida saab tõlgendada sd ühikutes. Erandiks on olukord, kus analüüsi eesmärk on võrrelda erinevaid valimeid omavahel. Enamasti on kasulik standardiseerida andmed, mis mudelisse sisse lähevad, aga on võimalik ka standardiseerida koefitsiente kui selliseid.

st_coef = (unstand_coef x sd(X))/sd(Y)

Standardiseeritud andmete kasutamine muudab varieeruvuskomponentide fitte, aga jätab b koefitsientide fitid olemuselt samaks (see kehtib X-muutujate suvaliste lineaarsete transformatsioonide korral). Kui me jagame X-muutuja 2-ga, siis \(uus ~b_1 = 2 ~x~vana~ b_1\). Mudeli poolt seletamata varieeruvuse proportsioon ei muutu. Eelnev kehtib senikaua, kuni mudeli tõusud (\(b_1\)) ei ole vabaks lastud, st need ei varieeru klassist klassi.

Tsentreerimine (\(x_i - mean(x)\)) mõjutab \(b_0\) aga mitte \(b_1\) koefitsiente, mis võib rääkida selle meetodi kasuks üle standardiseerimise ((\(\frac {x_i - mean(x)}{sd(x)}\)), mis tekitab X muutujate jaotused, mille mean = 0 ja sd = 1.

NB! grupi tasemel tsentreerimine, ehkki vahest kasulik, töötab hoopis teistmoodi kui üle kõikide gruppide tsentreerimine ja viib täiesti erineva mudelini - sellest tuleks hoiduda, senikaua kui te ei tea täpselt, mida te teete.

Mitmetasemelised mudelid on erilised, sest nad hõlmavad mitut varieeruvuse allikat, ei eelda konsantset vigade jaotust, ning modelleerivad seoseid erinevate mudeli tasemete vahel.

20.1.1 Aegread

Aegridasid saab analüüsida mitmetasemilisena, kus korduvad mõõtmised (1. tase) on grupeeritud indiviidide sisse (2. tase). Nii saab analüüsida ka ebaühtlase ajavahemiku järel tehtud mõõtmisi.

Aegridade analüüsi lisaprobleem võrreldes tavalise mitmetasemelise mudeliga on, et me ei saa enam eeldada, et 1. taseme (indiviidi taseme) vead on üksteisest sõltumatud. Aegridade vaatluste vead on sageli ajas autokorreleeritud.

\(Y_{ti}\) - indiviidi i õpitulemus ajapunktis t.

\(T_{ti}\) - ajapunkt

\(X_{ti}\) - ajas muutuv covariaat - kas õpilane töötab

\(Z_t\) - ajast mittesõltuv kovariaat - sugu

1. tase (indiviidi tase):

\[Y_{ti} = \pi_{0i} + \pi_{1i} x T_{ti} + \pi_{2i} X_{ti} + e_{ti} \]

2. tase (üle indiviidie):

\[\pi_{0i} = \beta_{00} + \beta_{01} Z_t + u_{01}\]

\[\pi_{1i} =\beta_{10} + \beta_{11} Z_t + u_{11}\]

\[\pi_{2i} = \beta_{20} + \beta_{21} Z_t + u_{21}\]

Oluline punkt: aegridade modelleerimisel pakub meile sageli huvi ka ka korrelatsioon mudeli tõusu ja intercepti vahel. Kahjuks sõltub see näitaja sellest, millises skaalas me ajamuutuja mudelisse sisse anname. Oluline on tagada, et ajaskaala nullpunkt on mõtekas.

To model growth - polynomial, logistic curve (first slow change, then quick, then slow again). Logistic parameters have meaning! Cubic polynomial approximates logistic and exponential curves - but here interpretation is on the level of some predicted growth curves.

https://facebook.github.io/prophet sessoonsete andmete fittimine ennustavasse mudelisse

https://github.com/nwfsc-timeseries kogu aegridade analüüsi pakette

library(coda)
#library(R2jags)
library(gridExtra)
library(broom)

20.1.2 Temporaalne autokorrelatsioon

eeldus: Mida lähemal on 2 ajapunkti üksteisele, seda suurem on nende vaheline korrelatsioon (ja residuaalide vaheline korrelatsioon). Tavaline lm eeldab, et see korrelatsioon = 0. Seda korrelatsiooni saab kas hinnata, või selle vastu võidelda. Meie teeme siin viimast.

Brms mudel näeb välja niimoodi

data.temporalCor.brms <-  brm(y ~ x, data = d, 
                              autocor = cor_ar(formula = ~year))

cor_ar() on brms funktsioon autokorrelatsiooni modelleerimiseks. selle formula on ühepoolne valem ~t või ~ t | g, mis annab ajakovariaadi t ja grupeeriva faktori g. Kui g on antud, siis modelleeritakse iga grupp iseseisvalt ja teistest gruppidest sõltumata (gruppide vahel on korrelatsioon 0).

Teine võimalus inkorporeerib mudelisse AR1 residuaalide autokorrelatsioonistruktuuri, kus korrelatsiooni eksponent väheneb ajas lineaarselt. Me eeldame, et see vähenemine toimub samamoodi sõltumata sellest, millises ajavahemikus me parasjagu oleme (statsionaarsuse eeldus).

data.temporalCor.brms = brm(y ~ x, data = d, 
                            autocor = cor_ar( ~year, cov = TRUE))

Lihtsuse mõttes eeldame, et iga ajapunkti oodatud väärtus = tavaline lin prediktor + autokorrelatsiooni parameeter (\(\rho\)) korrutatuna eelmise vaatluse residuaaliga + tavapärane sõltumatu müra (\(\sigma^2\)).

20.2 mitmetasemeline mudel R-i mudelikeeles

Kui meie muutujad andmetabelis “data” on y = õpilase testiskoor, x = katsetingimus (binaarne faktor katse-kontroll, kalamaksaöli - platseebo), ja kool, siis “ühepajamudel” väljendub R-i mudelikeeles:

mudel <- lm(y ~ x, data=data)

ja mudel, kus iga kool on eraldi modelleeritud:

mudelid <- data %>% group_by(kool) %>% do(model = lm(y ~ x, data = .))

või purrr-i abil

data %>% split(.$kool) %>% map(~ lm(y ~ x, data = .)) %>% map(summary) %>% map_dfr(~ broom::glance(.), .id = "kool")

Seevastu hierarhiline mudel kirjutatakse kui

mudel <- lme4::lmer(y ~ x + (1 + x | kool), data=data)

või

mudel <- lme4::lmer(y ~ x + (1 | kool), data=data)

Esimesel juhul modelleeritakse igale koolile nii tõus kui intercept ja teisel juhul modelleeritakse igale koolile ainult intercept, seeläbi eeldades, et kõikidel koolidel on mudelis sama tõus, ehk kalamaksaõli efekt (ES = testitulemus kalamaksaõli grupis - testitulemus platseebogrupis). Intercept tähendab sellises mudelis enamasti baastaset (kontrolltingimus) ja tõus tähendab katseefekti (katsetingimus - kontrolltingimus). Seega eeldab teine mudel, et igas grupis võib küll olla oma baastase, aga katsefekt sellest ei muutu.

Lisaks, mudel

mudel <- lme4::lmer(y ~ x + (1 + x || kool), data=data)

modelleerib igale koolile tõusu ja intercepti lisaeeldusega, et tõusude ja interceptide vaheline korrelatsioon puudub. Ilma selle eelduseta püüab mudel selle korrelatsiooni andmete põhjal leida. Kui andmeid on liiga vähe või mudel on liiga keeruline või korrelatsiooni võimalik esinemine tundub teadulsikult väga väheusutav, võib korrelatsiooni hindamisest loobuda, aga muidu tasub seda siiski hinnata.

mudel <- lme4::lmer(y ~ x + (1 + x | kool) + (1 + x | linn), data=data)

Kui meil on mudelis rohkem kui 2 taset, kirjutame need sõltumata sellest, kas tasemed on hierarhiliselt üksteise sees (õpilane - kool - linn) või mitte (patsient - haigla - ravimi batch)

mudel <- lme4::lmer(y ~ x + (1 + x | grupp1) + (1 + x | grupp2), data=data)

Kui esimesed 2 mudelit saab fittida lm() funktsiooniga, siis lihtne mitte-bayesiaanlik alternatiiv hierarhilise mudeli tarbeks on lme4 pakett (https://cran.r-project.org/web/packages/lme4/vignettes/lmer.pdf), mis on lihtsam, kiirem ja ebatäpsem ad hoc viis arvutada mitmetasemeliseid mudeleid, kui Stan. Selle eelis Stani ees on eelkõige kiirus ja puuduseks on väiksem paindlikus mudelite formuleerimisel ja see, et väikeste valimite ja väheste gruppide puhul töötab lme4 algoritm palju halvemini, kui bayesi lahendused. Seega kasutame me pigem Stani, kui lme4. Samas, suurepärane pakett nimega brms (https://cran.r-project.org/web/packages/brms/vignettes/brms_overview.pdf) suudab tõlkida lme4 mudeli kirjelduse otse Stani keelde ja seda mudelit seal jooksutada. Brms teeb elu magusaks (vt lisa 2).

Suurem sõltuvus valimi suurusest ja erinevatest lisaeeldustest võrreldes Bayesi mudelitega on see hind, mida ad hoc lahendused maksavad oma lihtsuse eest. Enamust klassikalisi teste (t test, chi ruut test, jms) võib vaadelda selliste ad hoc lahendustena, mis sageli lagunevad laiali väikesetel valimitel, samas kui bayes töötab väikeste valimitega hästi – tõsi küll, sõltudes väikeste valimite korral rohkem priorist ja andes seal realistlikult laiad usaldusintervallid.

20.3 Mitmetasemeliste mudelite lisaeeldused

Mitmetasandilised mudelid toovad sisse lisaeelduse, et lineaarsuse/normaalsuse jm eeldused kehtivad igal mudeli tasemel. Samuti, et kõik grupid tulevad samast statistilisest populatsioonist, ja vastavalt sellele on nad mudelis koondatud ühise priori alla. Mitmetasemelises mudelis töötab grupi tasemel mudel priorina indiviidi tasemel mudelile.

20.4 Mitmetasemeline mudel töötab korraga mitmel tasmel

Mudeli muudab mitmetasemeliseks see, et me määrame veamudelit kasutades mitte ainult indiviidi tasemel koefitsiente (1. tase), vaid anname neile koefitsientidele omakorda veamudeli (2. tase), mis modelleerib koefitsientide varieeruvust gruppide vahel. Selliseid tasemeid võib lisada põhimõtteliselt ükskõik kui palju. Kõrgema taseme mudel, lisaks sellele, et modelleerida gruppide vahelist varieeruvust, töötab ka priorina madalama taseme suhtes. Seega saab mudeli fittimisel 2. tase informatsiooni 1. tasemelt (andmete näol) ja samal ajal annab informatsiooni esimesele tasemele (priori kujul).

1. Mitmetasemelised mudelid modelleerivad eksplitsiitselt varieeruvust klasrtite sees ja klastrite vahel.

2. Nad modelleerivad indiviidi-tasemel regressioonikoefitsientide varieeruvust.

3. Nad võimaldavad paremini määrata indiviidi tasemel regressioonikoefitsiente endid, eriti kui erinevates gruppides on erinev arv indiviide.

Shrinkage

Oletame, et te plaanite reisi Kopenhaagenisse ja soovite sellega seoses teada, kui kallis on keskeltläbi õlu selle linna kõrtsides. Teile on teada õlle hind kolmes Kopenhaageni kõrtsis, mida ei ole just palju. Aga sellele lisaks on teile teada ka õlle hind 6-s Viini, 4-s Praha ja 5-s Pariisi kõrtsis. Nüüd on teil põhimõtteliselt kolm võimalust, kuidas sellele probleemile läheneda.

1. Te arvestate ainult Kopenhaageni andmeid ja ignoreerite teisi, kui ebarelevantseid. See meetod töötab hästi siis, kui teil on Kopenhaageni kohta palju andmeid (aga teil ei ole).

2. Te arvestate võrdselt kõiki andmeid, mis teil on — ehk te võtate keskmise kõikidest õllehindadest, hoolimata riigist. See töötab parimini siis, kui päriselt pole vahet, millisest riigist te oma õlle ostate, ehk kui õlu maksab igal pool sama palju. Antud juhul pole see ilmselt parim eeldus.

3. Te eeldate, et õlle hinna kujunemisel erinevates riikides on midagi ühist, aga et seal on ka erinevusi. Sellisel juhul tahate te fittida hierarhilise mudeli, kus teie hinnang õlle hinnale Kopenhaagenis sõltuks mingil määral (aga mitte nii suurel määral, kui eelmises punktis) ka teie kogemustest teistes linnades. Sama moodi, teie hinnang õlle hinnale Pariisis, Prahas jne hakkab mingil määral sõltuma kõikide linnade andmetest.

Kui teil on olukord, kus te mõõdate erinevaid gruppe, mis küll omavahel erinevad, aga on ka teatud määral sarnased (näiteks testitulemused grupeerituna kooli kaupa), siis on mõistlik kasutada kõikide gruppide andmeid, et adjusteerida iga grupi spetsiifilisi parameetreid. Seda adjusteerimise määra kutsutakse “shrinkage”.

Shrinkage toimub parameetri keskväärtuse suunas ja mingi grupi shrinkage on seda suurem, mida vähem on selles grupis liikmeid ja mida kaugemal asub see grupp kõikide gruppide keskväärtusest. See viib shrinkage koefitsientide kallutatusele (bias), aga samas ka suuremale täpsusele (precision). See tähendab, et shrinkage koefitsiendi hinnang on keskeltläbi lähemal tõelisele koefitsiendi väärtusele kui hannang tavalisele ühetasandilise mudeli koefitsiendile.

Shrinkage on põhimõtteliselt sama nähtus, mis juba Francis Galtoni poolt avastatud regressioon keskmisele. Regressioon keskmisele on stohhastiline protsess kus, olles sooritanud n mõõtmist ja arvutanud nende tulemuste põhjal efekti suuruse, see valimi ES peegeldab nii tegelikku ES-i kui juhuslikku valimiviga. Kui valimivea osakaal ES-s on suur, siis lisamõõtmised vähendavad keskeltläbi efekti suurust. Shrinkage erineb sellest ainult selle poolest, et lisamõõtmised meenutavad ainult osaliselt algseid mõõtmisi.

Kasutades hierarhilisi mudeleid saab võidelda ka valehäirete ehk mitmese testimise probleemiga. See probleem on lihtsalt sõnastatav: kui te sooritate palju võrdluskatseid ja statistilisi teste olukorras, kus tegelik katseefekt on tühine, siis tänu valimiveale annavad osad teie paljudest testidest ülehinnatud efekti. Seega, kui meil on kahtlus, et enamus võrdlusi on “mõttetud” ja me ei oska ette ennustada, millised võrdlused neist (kui üldse mõni) võiks anda tõelise teaduslikult mõtteka efekti, siis on lahendus kõiki saadud efekte kunstlikult pisendada kõikide efektide keskmise suunas. Mudeli kontekstis kutsutakse sellist lähenemist shrinkage-ks. Aga kui suurel määral seda teha? See sõltub nii sellest, kui palju teste me teeme, valimi suurusest, kui ka sellest, kuidas jaotuvad mõõdetud efektisuurused (milline on efektisuuruste varieeruvus testide vahel).

Bayesi lahendus on, et me lisame mudelisse veel ühe hierarhilise priori, mis kõrgub üle gruppide-spetsiifilise priori. Seega anname me olemasolevale priorile uue kõrgema taseme meta-priori, mis tagab, et informatsiooni jagatakse gruppide vahel ja samal ajal ka gruppide sees. Sellise lahenduse õigustus on, et me usume, et erinevad alam-grupid pärinevad samast üli-jaotusest ja neil on omavahel midagi ühist (ehkki alam-gruppide vahel võib olla ka reaalseid erinevusi). Näiteks, et kõik klassid saavad oma lapsed samast lastepopulatsioonist, aga siiski, et leidub ka eriklasse eriti andekatele.

Selline mudel tagab, et samamoodi nagu mudeli ennustused individaalsete andmepunktide kohta iga alam-grupi sees “liiguvad lähemale” oma alam-grupi keskmisele, samamoodi liiguvad ka alam-gruppide keskmised lähemale üldisele grupi keskmisele. Selle positiivne mõju on valealarmide vähendamine ja oht on, et me kaotame ka tõelisi efekte. Bayesi eelis on, et see oht realiseerub ainult niipalju, kuipalju meie mudel ei kajasta reaalset katse struktuuri. Klassikalises statistikas rakendatavad multiple testingu korrektsioonid (Bonfferroni, ANOVA jt) on kõik teoreetiliselt kehvemad.

Lihtsaim shrinkage mudeli tüüp on mudel, kus me laseme vabaks interceptid, aga mitte tõusunurgad. Igale klastrile vastab mudelis oma intercepti parameeter ja oma intercepti prior. Lisaks annab mudel meile fittimise käigus valimi andmete põhjal ise parameetrid kõrgema taseme priorisse, mis on ühine kõikidele interceptidele. Seega me määrame korraga interceptide parameetrid ja kõrgema taseme priori parameetrid, mis tähendab, et informatsioon liigub mudelit fittides mõlemat pidi — mööda hierarhiat alt ülesse ja ülevalt alla. Selline mudel usub, et erinevate koolide keskmine tase erineb (seda näitab iga kooli intercept), aga juhul kui me mõõdame näiteks kalamaksaõli mõju õppeedukusele, siis selle mõju suurus ei erine koolide vahel (kõikide koolide tõusuparameetrid on identsed).

Shrinkage kui nähtuse avastas Francis Galton 1870-ndatel aastatel. Galton ja tema sõbrad veetsid nimelt kümme aastat üle Inglismaa taimi kasvatades ja mõõtes erinevate põlvkondade seemnete suurusi. Eesmärk oli luua tühjale kohale uus teadus, pidevate tunnuste geneetika, ja katsete tulemus oli rabav. Nimelt leiti tugev seaduspära, mille kohaselt suurte seemnetega emataimede tütred andsid keskeltläbi väiksemaid seemneid kui nende vanemad ja vastupidi, väikeste seemnetega emade tütred andsid keskeltläbi suuremaid seemneid. Galtoni usk, et ta on avastanud tähtsa bioloogiaseaduse, purunes ca 1885, kui ta pääses analüüsima tuhatkonna inimese pikkusi andmestikus, mis sisaldas vanemate ja täiskasvanud laste pikkusi, ning leidis seal sama nähtuse. Sertifitseeritud geeniusena mõistis Galton, et ta ei olnud avastanud mitte niivõrd geneetikaseaduse, vaid peaaegu, et loogikaseaduse. Tema enda sõnadega: The average regression of the offspring to a constant fraction of their mid-parental deviations, is now shown to be a perfectly reasonable law which might have been deductively foreseen. It is of so simple a character that I have made an arrangement with pulleys and weights by which the probable average height of the children of known parents can be mechanically reckoned. (vt joonis). Sellega avastas Galton regressiooni keskmisele, mis on sisuliselt sama asi, mis shrinkage. Galton nägi, et shrinkagel on järgmised omadused: 1. “The mean filial regression towards mediocrity was directly proportional to the parental deviation from it.” Ehk, mida kaugemal on vanemad keskmisest, seda suurema amplituudiga on nende laste shrinkage 2. “The child inherits partly from his parents, partly from his ancestry. …the further his genealogy goes back, the more numerous and varied will his ancestry become … Their mean stature will then be the same as that of the race; in other words, it will be mediocre.” Ehk, shrinkage toimub alati, kui tunnuse väärtus ei ole deterministlikult määratud (shrinkage taandub korrelatsioonile vanemate ja laste varieeruvuse vahel) 3. “This law tells heavily against the full hereditary transmission of any gift. The more exceptional the amount of the gift, the more exceptional will be the good fortune of a parent who has a son who equals him in that respect.” Ehk, pidevate tunnuste korral on korrelatsioon alati <1 & >-1 4. “The law is even-handed; it levies the same heavy succession-tax on the transmission of badness as well as of goodness. If it discourages the extravagant expectations of gifted parents that their children will inherit all their powers, it no less discountenances extravagant fears that they will inherit all their weaknesses and diseases.” Ehk shrinkage töötab võrdselt mõlemas suunas (ülevalt alla ja alt üles, aga ka vanematelt lastele ja lastelt vanematele). Seega ei ole shrinkage ajas toimuv, põhjuslik, ega isegi mitte füüsikaline protsess, vaid tõenäosusteooriast tulenev loogiline paratamatus. Samamoodi nagu shrinkage esineb vanemate-laste vahel esineb see ka valimi-kordusvalimi vahel kõigi valimite keskmise suunas (valimiefektid taanduvad välja sedamõõda, kuidas valimeid juurde tuleb). Ja samamoodi, kui me võtame valimi testitulemusi mitmest koolist, siis eeldusel, et õpilased on kõikides koolides sarnased (aga mitte identsed), toimub shrinkage kõikide koolide keskmise suunas. Seega, nihutades mingi kooli keskmist testitulemust koolide keskmise suunas, saame parema hinnangu selle kooli õpilaste teadmisetele kui pelgalt selles koolis õpilaste teadmisi mõõtes!

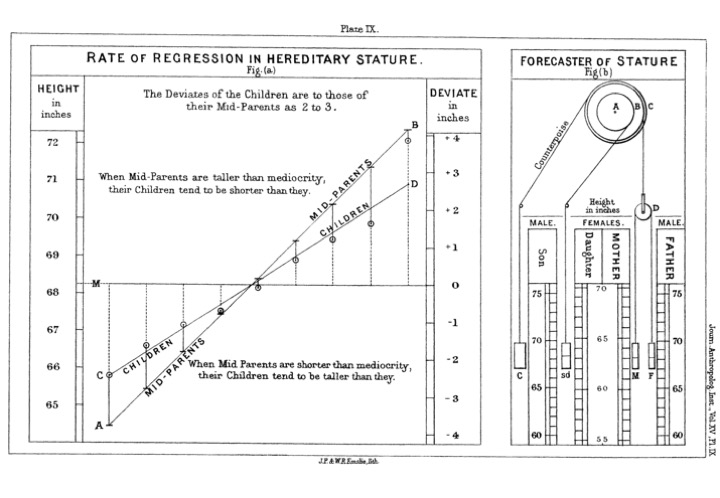
Joonis 11.3: (ref:Galton (1886), The Journal of the Anthropological Institute of Great Britain and Ireland, Vol. 15, pp. 246-263)

20.5 ANOVA-laadne mudel

Lihtne ANOVA on sageduslik test, mis võrdleb gruppide keskmisi mitmese testimise kontekstis. Siin ehitame selle Bayesi analoogi, mis samuti hindab gruppide keskmisi mitmese testimise kontekstis. Põhiline erinevus seisneb selles, et kui ANOVA punktennustus iga grupi keskväärtusele võrdub valimi keskväärtusega ja ANOVA pelgalt kohandab usaldusintervalle selle keskväärtuse ümber, siis bayesiaanlik mudel püüab ennustada igale grupile selle tegelikku kõige tõenäolisemat keskväärtust arvestades kõigi gruppide andmeid. Shrinkage-i roll on ekstreemseid gruppe “tagasi tõmmates” vähendada ebakindlust iga grupi keskmise ennustuse ümber. Shrinkage käigus tõmmatakse gruppe kõikide gruppide keskmise poole seda tugevamalt, mida kaugemal nad sellest keskmisest on. Sellega kaasneb paratamatult mõningane süstemaatiline viga, kus tõelised efektid tulevad välja väiksematena, kui nad tegelikult on. Kui ilma tegelike efektideta gruppide arv on väga suur võrreldes päris efektidega gruppidega, siis võib shrinkage meie pärisefektid sootuks ära kaotada. Kahjuks on see loogiline paratamatus; alternatiiviks on olukord, kus meie üksikud pärisefektid upuvad sama suurte pseudoefektide merre.

Ok, aitab mulast, laadime vajalikud raamatukogud ja andmed ning vaatame mis saab.

library(tidyverse)
library(stringr)
library(rethinking)
library(psych)

Andmed: The data contain GCSE exam scores on a science subject. Two components of the exam were chosen as outcome variables: written paper and course work. There are 1,905 students from 73 schools in England. Five fields are as follows.

1. School ID

2. Student ID

3. Gender of student

0 = boy

1 = girl

4. Total score of written paper

5. Total score of coursework paper

Missing values are coded as -1.

schools <- read_csv( "data/schools.csv")
schools <- schools %>%
  filter(complete.cases(.)) %>%
  mutate_at(vars(sex, school), as.factor)
## map2stan requires data.frame
class(schools) <- "data.frame"

Alustuseks mitte-hierarhiline mudel, mis arvutab keskmise score1 igale koolile eraldi. See on intercept-only mudel, mis tähendab, et me hindame testitulemuse keskväärtust kooli kaupa ja igale koolile sõltumatult kõigist teistest koolidest. Me ei püüa siin ennustada testitulemuste väärtusi x-i väärtuste põhjal. Selles mudelis on tavapärased ühetasemelised priorid, ainult mu on ümber nimetatud a_school-iks ja sellele on antud indeks [school], mis tähendab, et mudel arvutab a_school-i, ehk keskmise testitulemuse, igale koolile. Kuna siin puuduvad kõrgema taseme priorid, siis vaatab mudel igat kooli eraldi ja ühegi kooli hinnang ei arvesta ühegi teise kooli andmetega.

schoolm2 <- map2stan(
  alist(
    score1 ~ dnorm(mu, sigma),
    mu <- Intercept + v_Intercept[school],
    Intercept ~ dnorm(0, 50),
    v_Intercept[school] ~ dnorm(0, 50),
    sigma ~ dcauchy(0, 2)
  ), data = schools)

Vaata koefitsente.

precis(schoolm2, depth = 2)

Igale koolile antud hinnang on sõltumatu kõigist teistest koolidest.

Ja nüüd hierarhiline mudel, mis teab koolide vahelisest varieeruvusest. Siin leiab a_school-i priorist teise taseme meta-parameetri nimega sigma_school, millele on defineeritud oma meta-prior.

schoolm3 <- map2stan(alist(
  score1 ~ dnorm(mu, sigma),
  mu <- Intercept + v_Intercept[school],
  Intercept ~ dnorm(0, 50),
  v_Intercept[school] ~ dnorm(0, sigma_school),
  sigma_school ~ dcauchy(0, 2),
  sigma ~ dcauchy(0, 2)
), data = schools)

precis(schoolm3, depth = 2)

Nagu näha on sigma_school < sigma, mis tähendab, et koolide vaheline varieeruvus on väiksem kui õpilaste vaheline varieeruvus neis koolides. Seega sõltub testi tulemus rohkem sellest, kes testi teeb kui sellest, mis koolis ta käib. Loogika on siin järgmine: samamoodi nagu testitulemustel on jaotus õpilasekaupa, on neil ka jaotus koolikaupa. Koolikaupa jaotus töötab priorina õpilasekaupa jaotusele. Aga samas vajab kooli kaupa jaotus oma priorit — ehk meta-priorit. Seega saame me samast mudelist hinnangu nii testitulemustele kõikvõimalike õpilaste lõikes, kui ka kõikvõimalike koolide lõikes. Mudel ennustab ka nende koolide ja õpilaste tulemusi, keda tegelikult olemas ei ole, aga kes võiksid kunagi sündida.

Ning veel üks hierarhiline mudel, mis teab nii koolide skooride keskmiste varieeruvust kui koolide vahelist varieeruvust.

Võrdleme mudeleid.

compare(schoolm2, schoolm3)

Siit nähtub, et m3 on parim mudel, aga ka m2 omab mingit kaalu.

coeftab_plot(coeftab(schoolm2, schoolm3), cex = 0.5)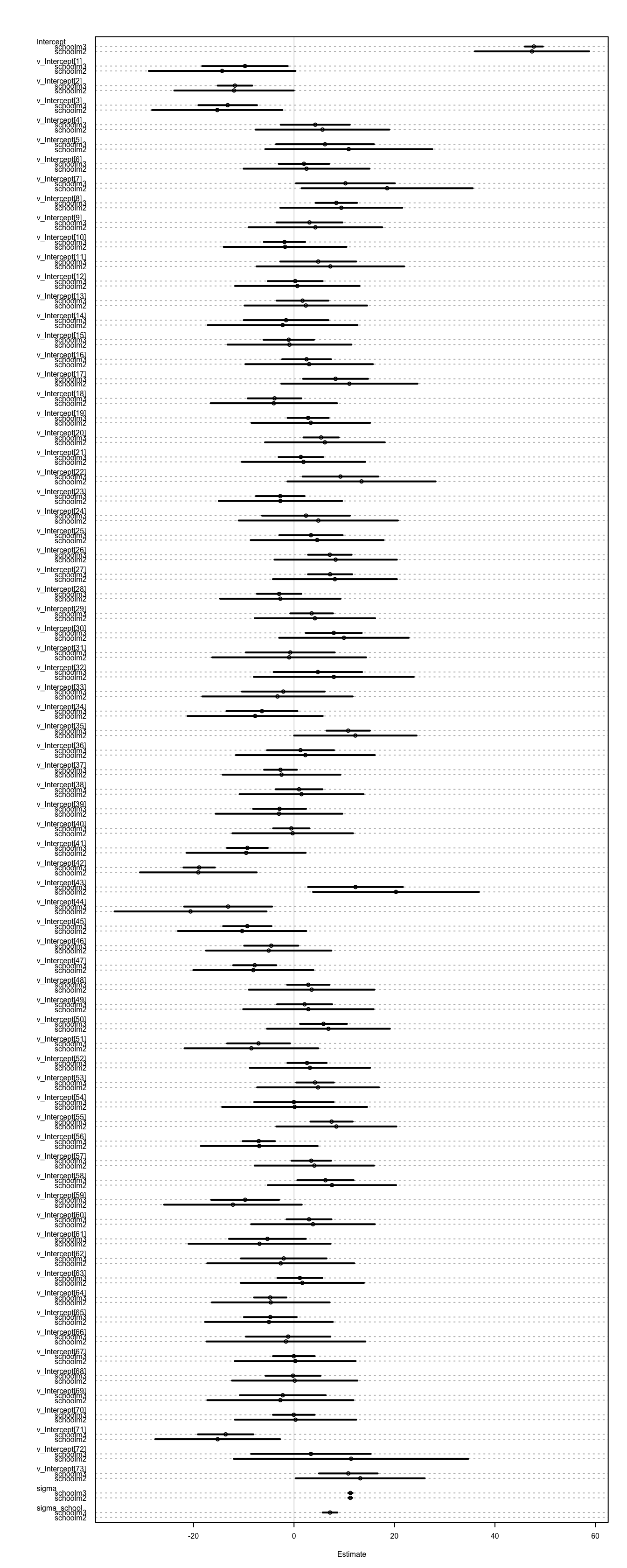

Joonis 4.6: Mudelite koefitsiendid.

Siin on hästi näha shrinkage m3 puhul võrreldes m2-ga, mis ei tee multiple testingu korrektsiooni. Nende koolide puhul, kus usaldusintervall on laiem, on ka suurem shrinkage (mudel võtab nende kohta suhteliselt rohkem infot teistest koolidest sest need koolid ise on mingil põhjusel suhteliselt infovaesed).

20.6 Vabad interceptid klassikalises regressioonimudelis

Ennustame score1 sõltuvust sex-ist. Küsimus: kui palju poiste ja tüdrukute matemaatikaoskused erinevad? Fitime mudeli, mis laseb vabaks intercepti. Selle mudeli eeldus on, et igal koolil on oma baastase (oma intercept), aga kõikide koolide efektid (mudeli tõusu-koefitsient) on identsed.

describe(schools)
#>         vars    n    mean      sd median trimmed   mad  min  max  range
#> school*    1 1523   38.36   19.98   40.0   38.84  23.7 1.00   73   72.0
#> student    2 1523 1016.45 1836.14  129.0  628.65 124.5 1.00 5516 5515.0
#> sex*       3 1523    1.59    0.49    2.0    1.61   0.0 1.00    2    1.0
#> score1     4 1523   46.50   13.48   46.0   46.68  13.3 0.60   90   89.4
#> score2     5 1523   73.38   16.44   75.9   74.65  16.5 9.25  100   90.8
#>          skew kurtosis    se
#> school* -0.18    -1.08  0.51
#> student  1.69     0.98 47.05
#> sex*    -0.37    -1.87  0.01
#> score1  -0.12    -0.05  0.35
#> score2  -0.75     0.51  0.42

Me kasutame prediktorina binaarset kategoorilist muutujat. See on analoogiline olukord ANOVA mudelile, mis võtab arvesse multiple testingu olukorra, mis meil siin on.

schools_f1 <- glimmer(score1 ~ sex + (1 | school), data = schools)
#> alist(
#>     score1 ~ dnorm( mu , sigma ),
#>     mu <- Intercept +
#>         b_sex1*sex1 +
#>         v_Intercept[school],
#>     Intercept ~ dnorm(0,10),
#>     b_sex1 ~ dnorm(0,10),
#>     v_Intercept[school] ~ dnorm(0,sigma_school),
#>     sigma_school ~ dcauchy(0,2),
#>     sigma ~ dcauchy(0,2)
#> )

Kuna glimmeri priorite parametriseeringud on vales skaalas (liiga väikesed), muudame neid nii, et intercept (keskmine testitulemus üle koolide) oleks tsentreeritud 50-le (max testi tulemus on 100) ja standardhälve on 20. Igaks juhuks tõstame veidi ka beta koefitsiendi priori sigmat. v_intercept peaks olema alati nullile tsentreeritud.

Glimmeri väljundis on sama palju koolide veerge, kui palju on erinevaid koole, miinus üks. Selline binaarne numbriline väljund on Stani-le vajalik. Seega ei saa me faktortunnuste korral kasutada algset andmetabelit.

head(schools_f1$d)

schools_m1 <- map2stan(alist(
    score1 ~ dnorm( mu , sigma ),
    mu <- Intercept + b_sex1*sex1 + v_Intercept[school],
    Intercept ~ dnorm(50, 20),
    b_sex1 ~ dnorm(0, 15),
    v_Intercept[school] ~ dnorm(0, sigma_school),
    sigma_school ~ dcauchy(0,2),
    sigma ~ dcauchy(0,2)
), data = schools_f1$d) # use the data table generated by glimmer() 
#glimmer converts factors to Stan-eatable form.

Siin on v_Intercept kooli-spetsiifiline korrektsioonifaktor, mis tuleb liita üldisele Interceptile. mean(v_Intercept) == 0. Me eeldame, et korrektsioonid on normaaljaotusega. Alternatiivne viis seda mudelit kirjutada oleks mu <- Intercept[school] + b_sex1*sex1 ja see töötab smamoodi (nüüd on iga kooli intercept kohe eraldi).

plot(precis(schools_m1, depth = 2), cex = 0.5)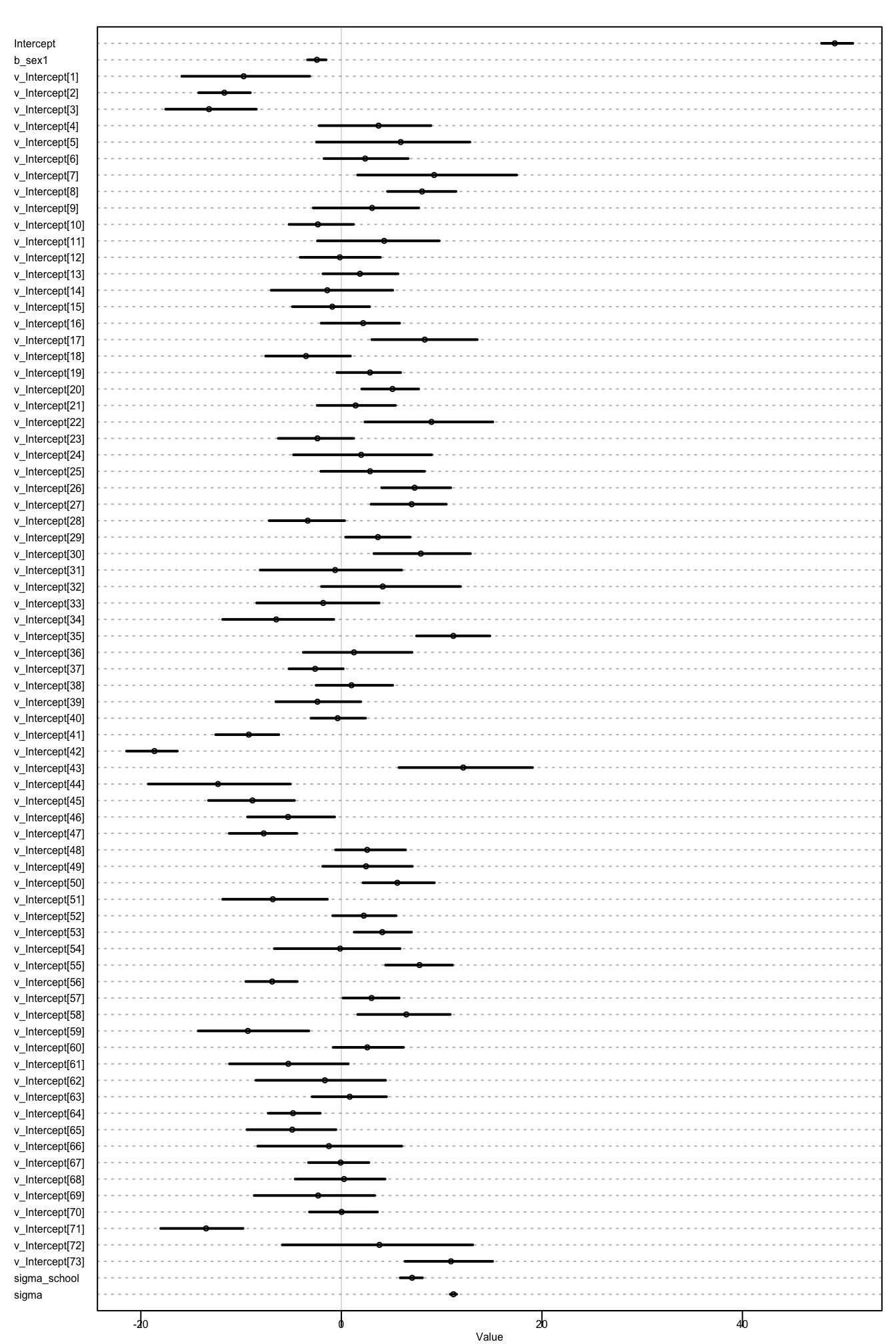

Joonis 17.2: Mudeli koefitsiendid

precis(schools_m1)
#>               Mean StdDev lower 0.89 upper 0.89 n_eff Rhat
#> Intercept    49.21   0.98      47.89      51.01   227    1
#> b_sex1       -2.44   0.60      -3.37      -1.52  1000    1
#> sigma_school  7.06   0.71       5.87       8.09  1000    1
#> sigma        11.18   0.20      10.85      11.50  1000    1

sex = 1 ehk sex1 on tüdruk.

Intercept annab siin sex = 0 (poisid) keskmise skoori kooli kaupa (kui liita üldisele interceptile kooli-spetsiifiline intercept). Kui tahame näiteks hinnangut 2. kooli tüdrukute skoorile (ehk tõelisele matemaatikavõimekusele) siis:

Intercept + b_sex1 + intercept[2]

annab meile selle posteeriori. Poistele sama 2. kooli kohta:

Intercept + intercept[2]

Ja poiste-tüdrukute erinevus skooripunktides võrdub

b_sex1

Arvutame siis kooli nr 2 tüdrukute keskmise skoori posteeriori.

schools_m1_samples <- as.data.frame(schools_m1@stanfit)
school_2_girls <- schools_m1_samples$Intercept + 
  schools_m1_samples$b_sex1 + 
  schools_m1_samples$`v_Intercept[2]`
## Plot density histogram of intercepts
dens(school_2_girls)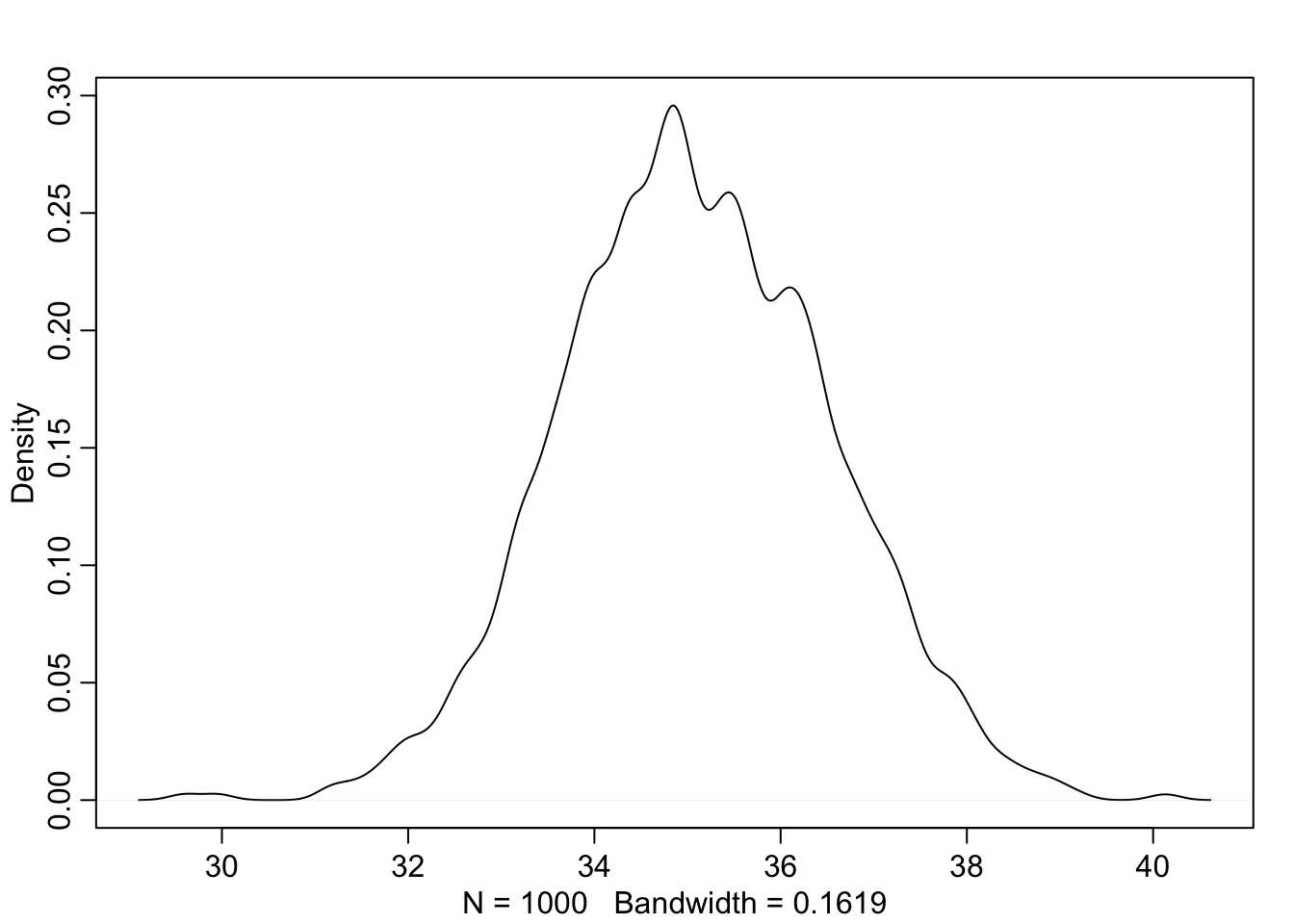

Joonis 20.1: Tüdrukute skoori posteerior

Ja Poiste oma

school_2_boys <- schools_m1_samples$Intercept + 
  schools_m1_samples$`v_Intercept[2]`
## Plot density histogram of intercepts
dens(school_2_boys)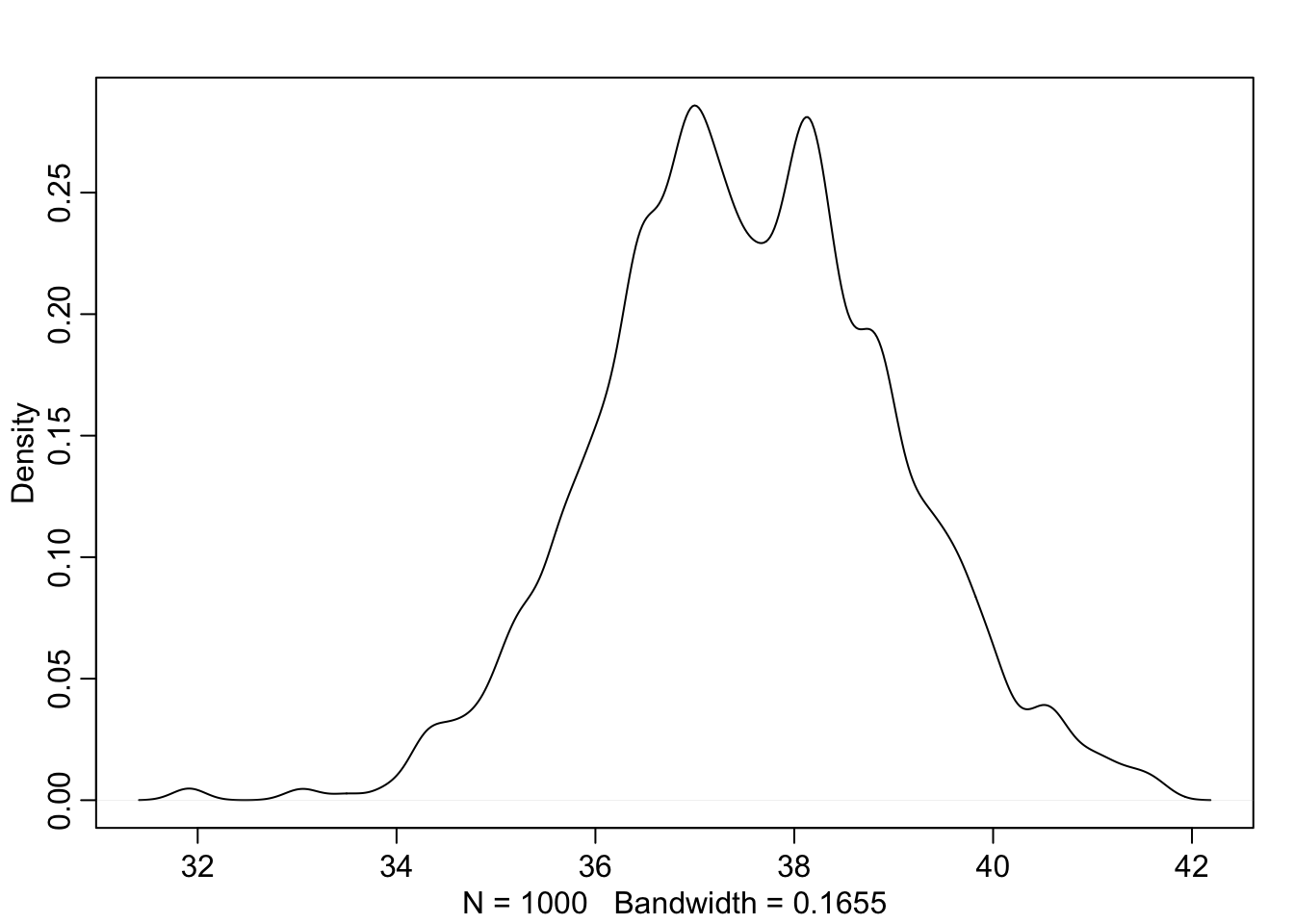

Joonis 19.3: Poiste skoori posteerior.

Siin on eeldus, et kõikides koolides on sama poiste ja tüdrukute vaheline erinevus (b_sex1), kuid erinevad matemaatikateadmiste baastasemed (mudeli intercept on koolide vahel vabaks lastud, kuid tõus mitte).

20.7 Vabad tõusud ja interceptid

Milline näeb välja mudel, kus me laseme vabaks nii intercepti kui tõusu?

schools_f2 <- glimmer(score1 ~ sex + (1 + sex | school), data = schools)
#> alist(
#>     score1 ~ dnorm( mu , sigma ),
#>     mu <- Intercept +
#>         b_sex1*sex1 +
#>         v_Intercept[school] +
#>         v_sex1[school]*sex1,
#>     Intercept ~ dnorm(0,10),
#>     b_sex1 ~ dnorm(0,10),
#>     c(v_Intercept,v_sex1)[school] ~ dmvnorm2(0,sigma_school,Rho_school),
#>     sigma_school ~ dcauchy(0,2),
#>     Rho_school ~ dlkjcorr(2),
#>     sigma ~ dcauchy(0,2)
#> )

nüüd on meil lisaparameetrid v_sex1, mis annab tõusu igale koolile eraldi ning Rho-school, mis annab korrelatsiooni intercepti ja tõusu vahel. Nüüd me jagame informatsiooni erinevat tüüpi parameetrite, nimelt interceptide ja tõusude, vahel. Selleks ongi vaja Rho lisa-parameetrit. Nüüd ei modelleeri me intercepti ja tõusu enam 2 eraldi normaaljaotuste abil vaid ühe 2-dimensionaalse normaaljaotusega (mvnorm2).

Prior korrelatsioonile Interceptide ja tõusude vahel on rethinking::lkjcorr(). Selle ainus parameeter on K. Mida suurem K, seda rohkem on prior konsentreeritud 0 korrelatsiooni ümber. K = 1 annab tasase priori. Meie kasutame K = 2, mis töötab laia vahemiku mudelitega.

R <- rlkjcorr(1e4, K = 2, eta = 2)
dens(R[, 1, 2] , xlab = "correlation")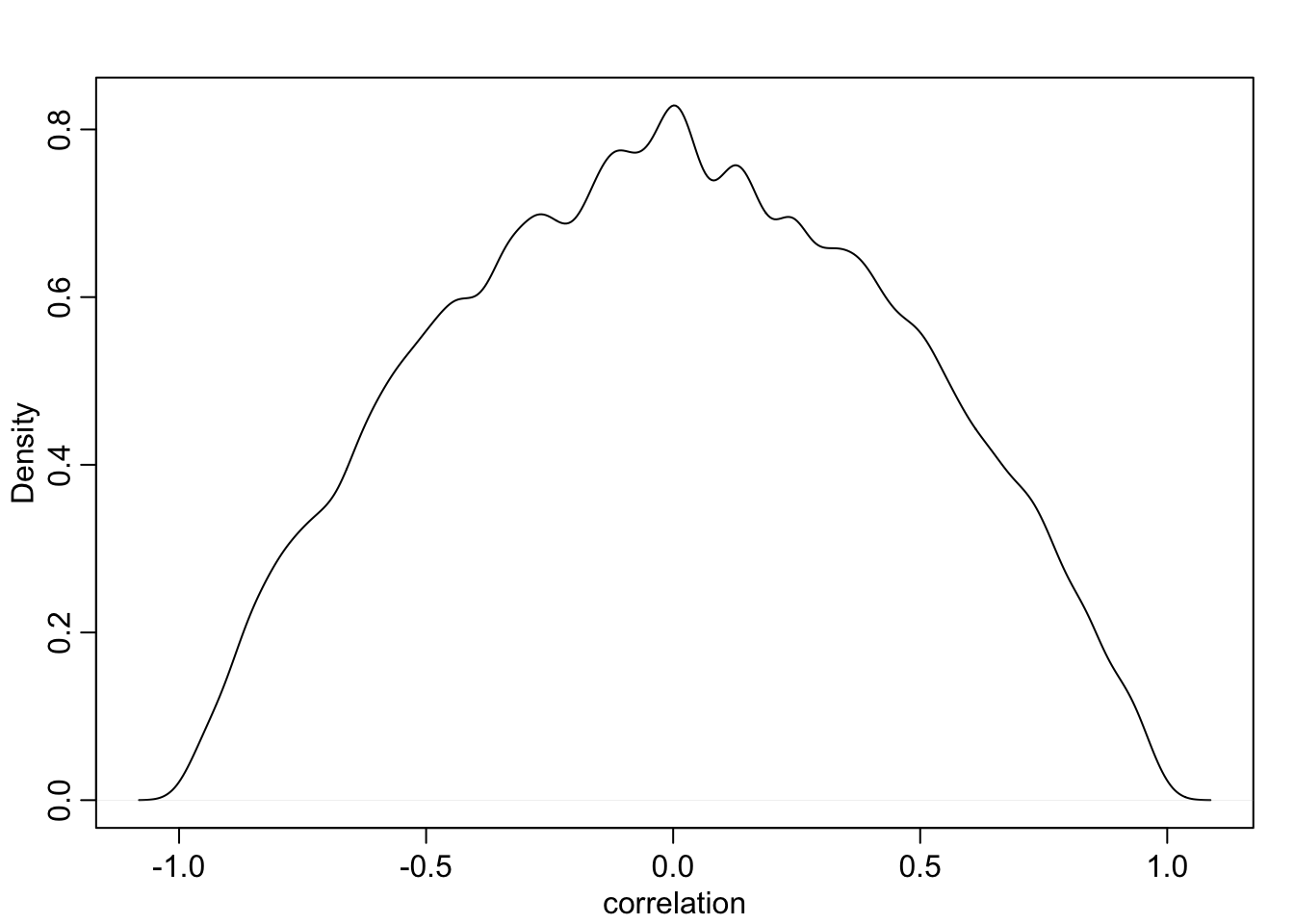

Joonis 4.8: Korrelatsiooni prior on nõrgalt informatiivne – suunab posteeriori eemale ekstreemsetest korrelatsioonidest.

schools_m2 <- map2stan(alist(
    score1 ~ dnorm( mu , sigma ),
    mu <- Intercept +
        b_sex1*sex1 +
        v_Intercept[school] +
        v_sex1[school]*sex1,
    Intercept ~ dnorm(50, 20),
    b_sex1 ~ dnorm(0, 20),
    c(v_Intercept,v_sex1)[school] ~ dmvnorm2(0, sigma_school, Rho_school),
    sigma_school ~ dcauchy(0,2),
    Rho_school ~ dlkjcorr(2),
    sigma ~ dcauchy(0,2)
), schools_f2$d)

plot(precis(schools_m2, depth = 2), cex = 0.5)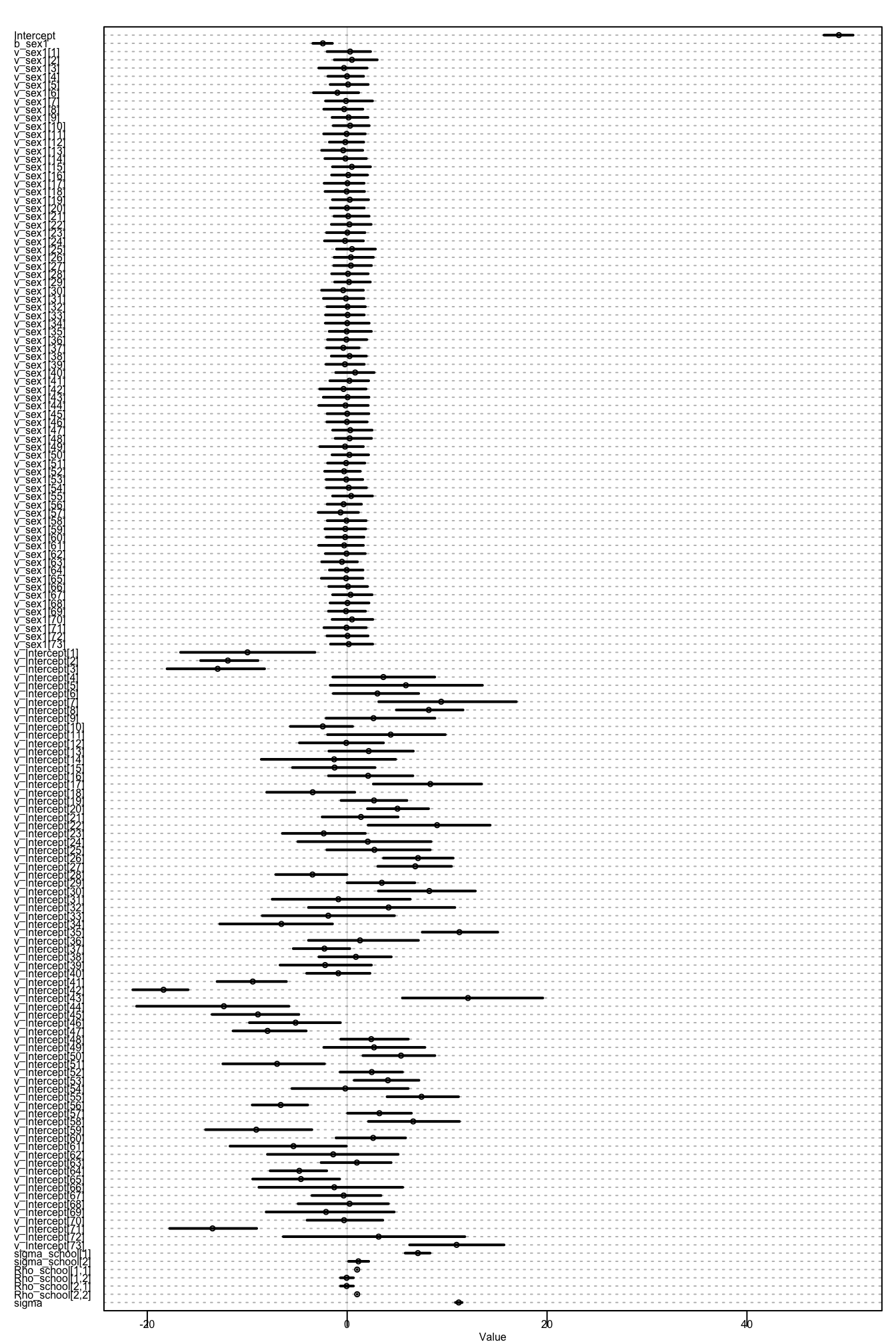

Joonis 20.2: Mudeli m2 koefitsiendid.

Posteerior korrelatsioonile intercepti ja tõusu vahel:

schools_m2_samples <- extract.samples(schools_m2)
df1 <- schools_m2_samples$Rho_school %>% as.data.frame()
#df1 #corr matrix- we need only the V2 col
dens(df1$V2)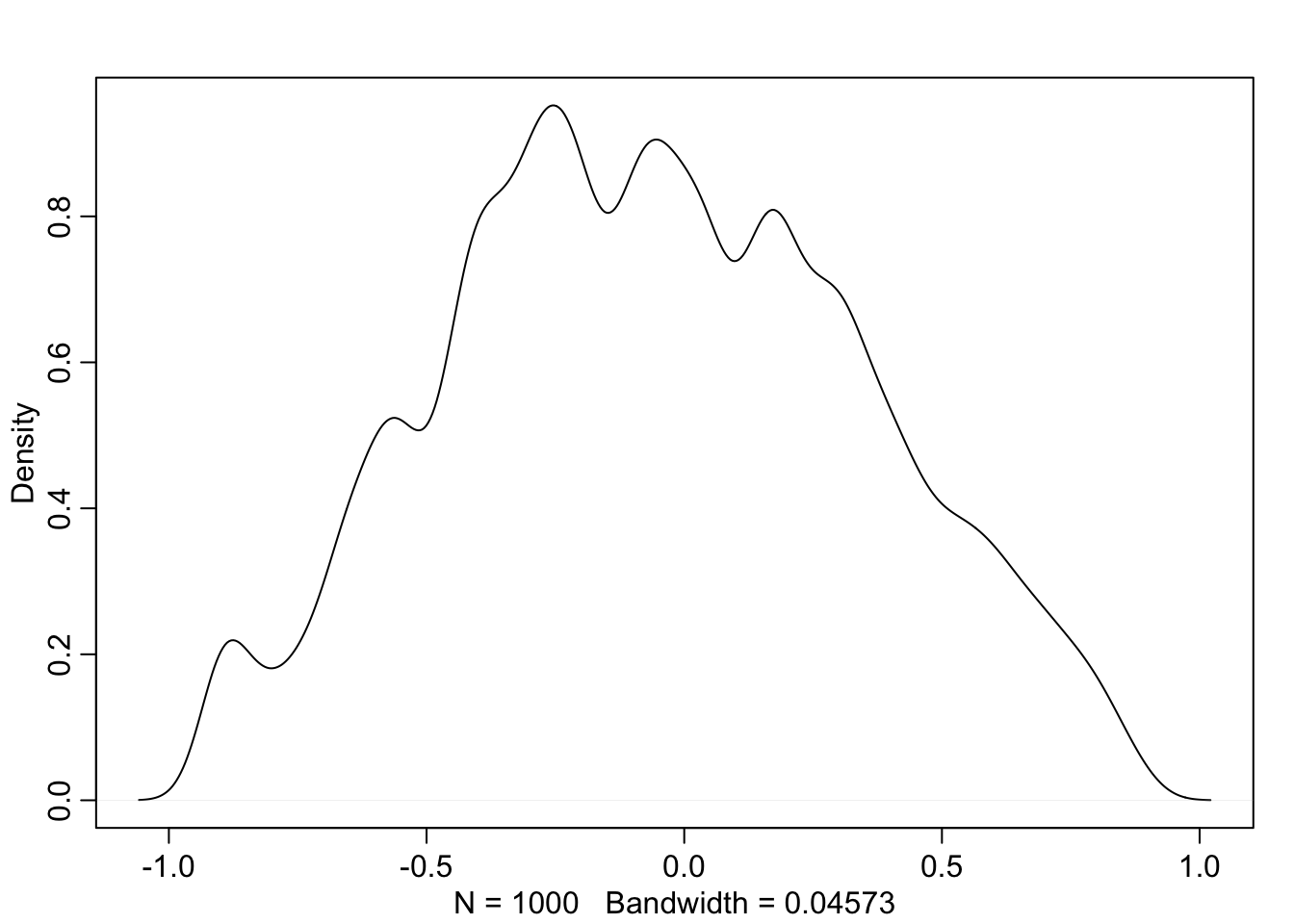

Joonis 19.4: Posteerior korrelatsioonile intercepti ja tõusu vahel.

Meil on negatiivne korrelatsioon intercepti ja tõusu vahel. Seega, mida väiksem on poiste keskmine skoor koolis (=intercept), seda suurem om erinevus poiste ja tüdrukute skooride vahel (= tõus).

Nüüd saab 2. kooli skoori tüdrukutele valemiga:

Intercept + b_sex1 + v_intercept[2] + v_sex1[2]

Sama skoor poistele:

Intercept + v_intercept[2]

ja tüdrukute ja poiste erinevus 2. koolile:

b_sex1 + v_sex1[2]

tüdrukute-poiste erinevus üle kõikide koolide:

b_sex1

tüdrukute keskmine skoor üle kõikide koolide:

Intercept + b_sex1

ja poiste keskmine skoor üle kõikide koolide:

Intercept

Tõmbame mudelist ennustused 1., 2. ja 37. kooli poiste skooridele järgmisel semestril:

d.pred <- list(
  school = c(1, 2, 37),
  sex1 = 0
)

schools_sim <- rethinking::sim(schoolm2, data = d.pred) 
#> [ 100 / 1000 ]
[ 200 / 1000 ]
[ 300 / 1000 ]
[ 400 / 1000 ]
[ 500 / 1000 ]
[ 600 / 1000 ]
[ 700 / 1000 ]
[ 800 / 1000 ]
[ 900 / 1000 ]
[ 1000 / 1000 ]
pred.p <- apply(schools_sim, 2, mean)
pred.p.PI <- apply(schools_sim, 2 , PI)

NB! kasutades rethinking::sim() saame me enustused andmepunktide (üksikute poiste tasemel). Antud juhul jääb ennustuse kohaselt esimeses koolis 89% individuaalseid skoore vahemikku 61-132 punkti 200-st võimalikust.

Kui meid huvitab hoopis nende koolide keskmine skoor järgmisel semestril, siis kasuta rethinking::sim() asemel rethinking::link() funktsiooni.

schools_sim <- link(schools_m2, data = d.pred) 
#> [ 100 / 1000 ]
[ 200 / 1000 ]
[ 300 / 1000 ]
[ 400 / 1000 ]
[ 500 / 1000 ]
[ 600 / 1000 ]
[ 700 / 1000 ]
[ 800 / 1000 ]
[ 900 / 1000 ]
[ 1000 / 1000 ]
pred.p <- apply(schools_sim, 2, mean)
pred.p.PI <- apply(schools_sim, 2, PI)
pred.p.PI
#>     [,1] [,2] [,3]
#> 5%  32.6 34.4 44.3
#> 94% 46.2 39.9 49.7

Esimeses koolis jääb keskmine poiste skoor 89% tõenäosusega vahemikku 33 kuni 46 punkti.

compare(schools_m1, schools_m2)
#>             WAIC pWAIC dWAIC weight   SE  dSE
#> schools_m1 11734  55.8   0.0    0.7 57.2   NA
#> schools_m2 11736  60.8   1.7    0.3 57.2 1.38

Tundub, et tõusude vabakslaskmine oli hea mõte. Ma saan hästi pihta, et erinevad koolid õpetavad matemaatikat erineva kvaliteediga. Aga miks peaks erinevates Inglismaa koolides olema erinev vahe poiste ja tüdrukute matemaatikateadmistel? Kas olukorras kus meil on hea kool, läheb see vahe väiksemaks või suuremaks? Tehke kindlaks!!! võrrelge graafiku slope vs. intercept.

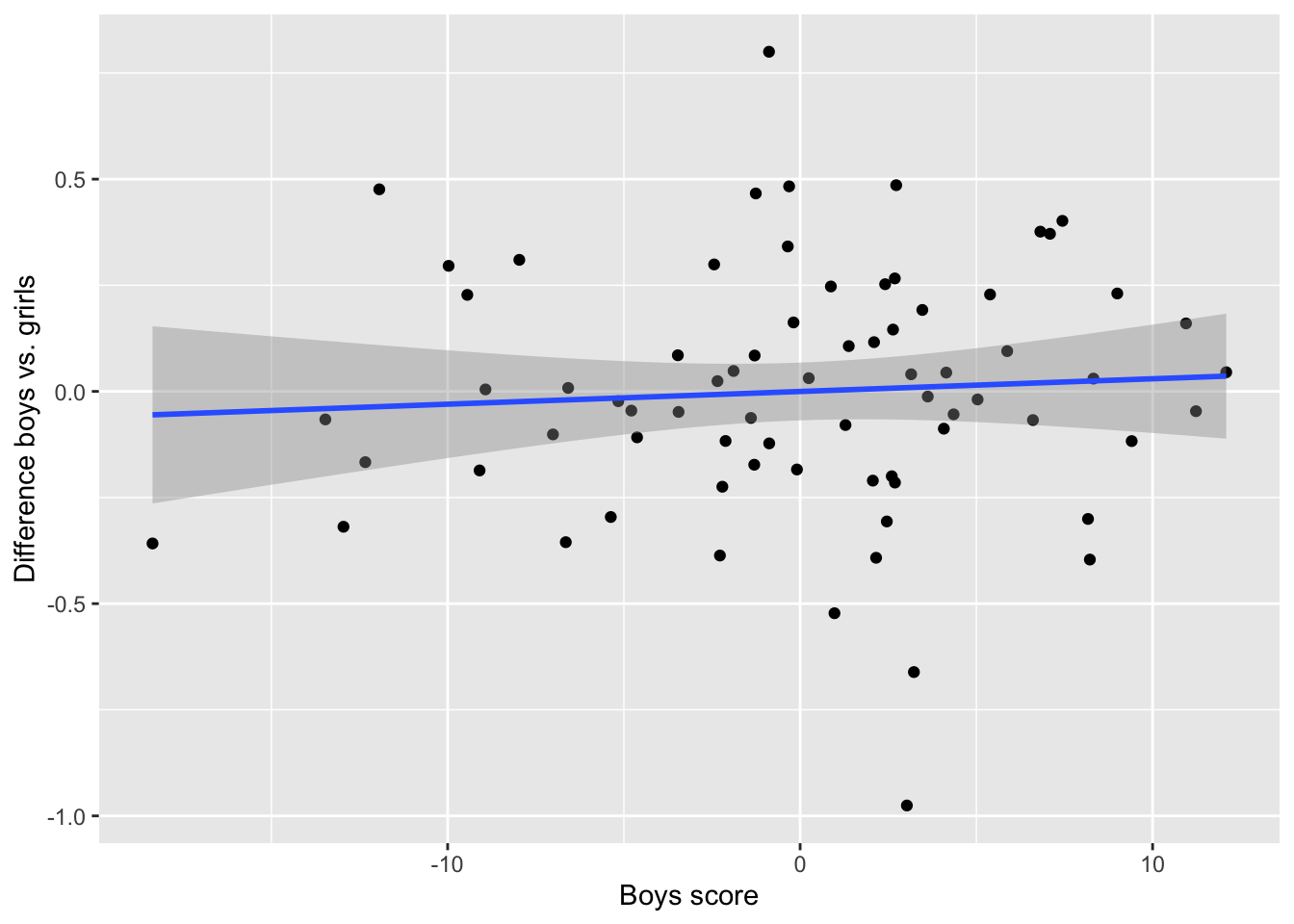
Joonis 16.13: mida suurem on koolis poiste skoor, seda väiksem on poiste ja tüdrukute erinevus

Tõepoolest: mida suurem on koolis poiste skoor (parem kool), seda väiksem on poiste ja tüdrukute erinevus. Aga seos on kaunis nõrk!

Muide sel joonisel tähendavad negatiivsed väärtused alla keskmist väärtust, mitte tingimata negatiivset erinevust või negatiivset skoori. Miks?

Arvutage nüüd poiste ja tüdrukute keskmine skoor kooli kaupa ja vaadake uuesti sõltuvust samasse erinevusesse. Mis on õigem viis: kas fittida ilma interceptita mudel (nagu eelmises peatükis) ja kasutada otse selle koefitsiente või kasutada meie m2 mudelit ning arvutada selle mudeli koefitsientide põhjal uus statistik (kaalutud keskmine näiteks)? Miks?

20.8 Hierarhiline mudel pidevate prediktoritega

Siin püüame ennustada score1 mõju score2 väärtusele.

plot(schools$score2, schools$score1)
abline(lm(score1 ~ score2, data = schools))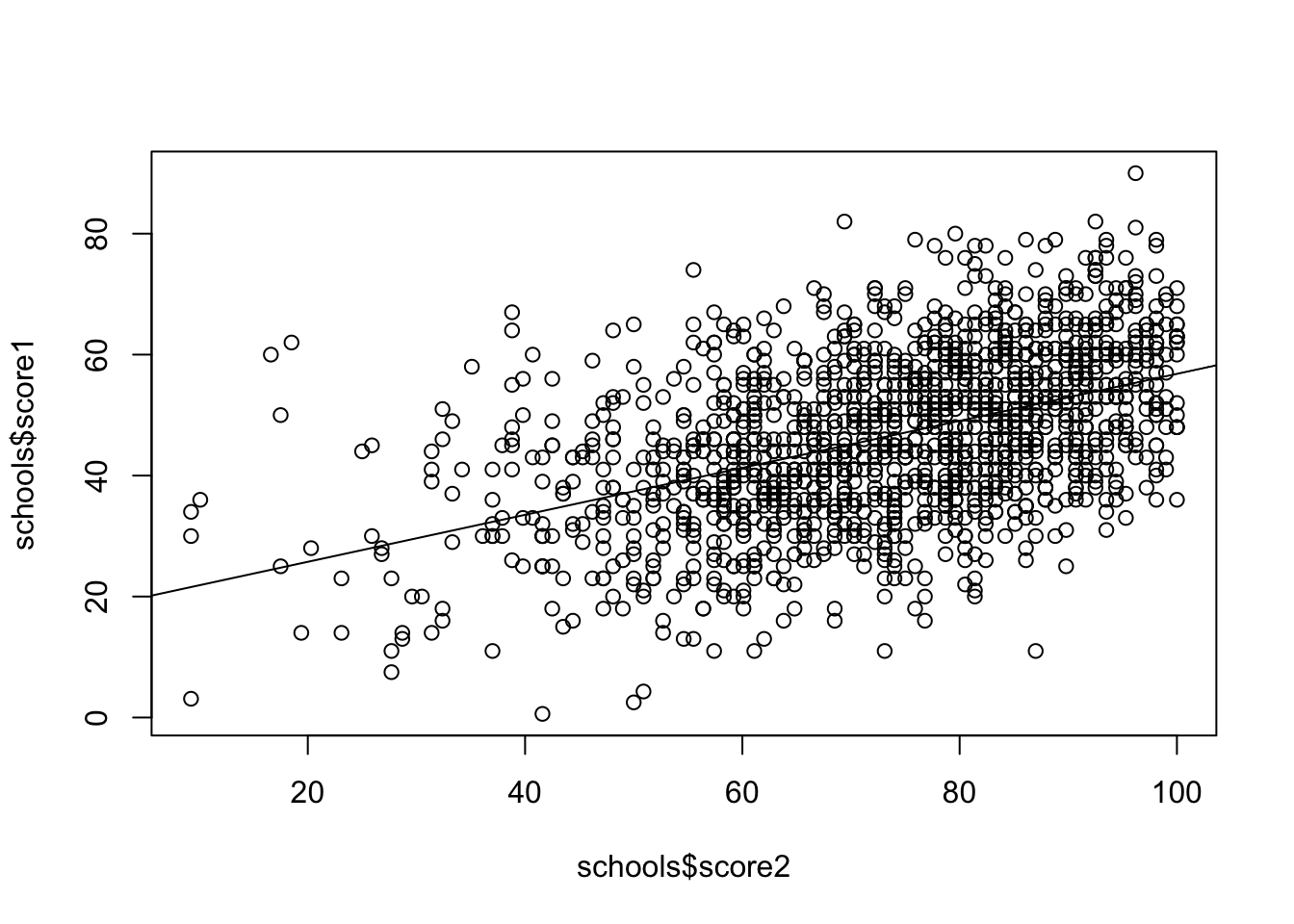

Joonis 20.3: score1 vs. score2

Kõigepealt lihtne regressioon lm() funktsiooniga (see ei ole hierarhiline mudel).

lm(score1 ~ score2, data = schools)
#> 
#> Call:
#> lm(formula = score1 ~ score2, data = schools)
#> 
#> Coefficients:
#> (Intercept)       score2  
#>      17.971        0.389

score2 tõus 1 punkti võrra tõstab score1-e 0.39 punkti võrra.

Modelleerime seost üle Bayesi hierarhilise mudeli, kus ainult Intercept on vabaks lastud.

glimmer(score1 ~ score2 + (1 | school), data = schools)
#> alist(
#>     score1 ~ dnorm( mu , sigma ),
#>     mu <- Intercept +
#>         b_score2*score2 +
#>         v_Intercept[school],
#>     Intercept ~ dnorm(0,10),
#>     b_score2 ~ dnorm(0,10),
#>     v_Intercept[school] ~ dnorm(0,sigma_school),
#>     sigma_school ~ dcauchy(0,2),
#>     sigma ~ dcauchy(0,2)
#> )

schoolm7 <- map2stan(alist(
    score1 ~ dnorm(mu, sigma),
    mu <- Intercept +
        b_score2 * score2 +
        v_Intercept[school],
    Intercept ~ dnorm(50, 50),
    b_score2 ~ dnorm(0, 10),
    v_Intercept[school] ~ dnorm(0, sigma_school),
    sigma_school ~ dcauchy(0, 2),
    sigma ~ dcauchy(0, 2)
), data = schools)

Siin ei ole individuaalsed interceptid tõlgenduslikult informatiivsed, aga nende sissepanek parandab mudeli ennustust beta koefitsiendile (beta läheb väiksemaks ja ebakindlus selle hinnangu ümber kasvab).

precis(schoolm7, depth = 2)

Siin tuleb beta veidi väiksem - 0.36. Kuna sigma_school < sigma, siis tundub, et koolide vaheline varieeruvus on väiksem kui laste vaheline varieeruvus (sigma on üle kõigi koolide). iga kooli baastase tuleb Intercept + v_Intercept[] aga selle mudeli järgi on kõikide koolide score2 ja score1 sõltuvus sama tugevusega.

Laseme siis ka tõusud vabaks

glimmer(score1 ~ score2 + (1 +  score2 | school), data = schools)
#> alist(
#>     score1 ~ dnorm( mu , sigma ),
#>     mu <- Intercept +
#>         b_score2*score2 +
#>         v_Intercept[school] +
#>         v_score2[school]*score2,
#>     Intercept ~ dnorm(0,10),
#>     b_score2 ~ dnorm(0,10),
#>     c(v_Intercept,v_score2)[school] ~ dmvnorm2(0,sigma_school,Rho_school),
#>     sigma_school ~ dcauchy(0,2),
#>     Rho_school ~ dlkjcorr(2),
#>     sigma ~ dcauchy(0,2)
#> )

schoolm5 <- map2stan(alist(
    score1 ~ dnorm( mu , sigma ),
    mu <- Intercept + b_score2 * score2 + 
      v_Intercept[school] + 
      v_score2[school] * score2,
    Intercept ~ dnorm(50, 25),
    b_score2 ~ dnorm(0, 10),
    c(v_Intercept, v_score2)[school] ~ dmvnorm2(0, sigma_school, Rho_school),
    sigma_school ~ dcauchy(0, 2),
    Rho_school ~ dlkjcorr(2),
    sigma ~ dcauchy(0, 2)
), data = schools)

nüüd saame igale koolile arvutada oma intercepti ja oma tõusu (ikka samamoodi: Intercept + v_intercept[] ja b_score2 + v_score2[])

precis(schoolm5, depth = 2)

schoolm6 <- map2stan(alist(
  score1 ~ dnorm(mu , sigma),
  mu <- Intercept + b_score2 * score2,
  Intercept ~ dnorm(50, 50),
  b_score2 ~ dnorm(0, 10),
  sigma ~ dcauchy(0, 2)
), data = schools)

m2 on selgelt parem mudel, kuigi m3 hinnangud interceptidele on suurema ebakindlusega. beta on nyyd 0.35

compare(schoolm7, schoolm6, schoolm5)
#>           WAIC pWAIC dWAIC weight   SE  dSE
#> schoolm5 11380  78.4   0.0      1 56.4   NA
#> schoolm7 11416  59.5  35.5      0 56.0 11.6
#> schoolm6 11862   3.3 482.0      0 54.6 41.6

0-mudel, mis on kõige kehvem, on kõige suurema betaga ja kõige väiksema ebakindlusega selle ümber. See on tavaline — hierarhiline mudel modelleerib ebakindlust paremini (realistlikumalt) ja vähendab üle-fittimise ohtu (beta tuleb selle võrra väiksem).

precis(schoolm7, depth = 2)