5 Kaks lineaarse mudeli laiendust

library(tidyverse)
library(scatterplot3d)
library(viridis)
library(ggeffects)
library(broom)
library(car)

5.1 Mitme sõltumatu prediktoriga mudel

Esiteks vaatame mudelit, kus on mitu prediktorit $x_1$, $x_2$, … $x_n$, mis on aditiivse mõjuga. See tähendab, et me liidame nende mõjud, mis omakorda tähendab, et me usume, et $x_1$ … $x_n$ mõjud y-i väärtusele on üksteisest sõltumatud. Mudel on siis kujul

\[y = a + b_1x_1~ + b_2x_2~ +~ ... +~ b_nx_n\]

Mitme prediktoriga mudeli iga prediktori tõus (beta koefitsient) ütleb, mitme ühiku võrra ennustab mudel y muutumist juhul kui see prediktor muutub ühe ühiku võrra ja kõik teised prediktorid ei muutu üldse (Yule, 1899).

Milliseid muutujaid (regressoreid) peaks üks hea lineaarne mudel sisaldama, milliseid peaks me mudelist välja viskama ja milliseid igal juhul sisse panema? Matemaatiliselt põhjustab regressorite eemaldamine ülejäänud regressorite koefitsientide ebakonsistentsust, välja arvatud siis, kui (i) välja visatud regressorid ei ole korreleeritud sisse jäetud regressoritega või (ii) välja vistatud regressorite koefitsiendid võrduvad nulliga, mis muudab nad ebarelevantseteks. Kuidas sa tead, et kõik vajalikud regressorid on sul üldse olemas (olematuid andmeid ei saa ka mudelisse lisada)? Loomulikult ei teagi, mis tähendab lihtsalt, et mudeldamine on keeruline protsess, nagu teaduski. Pane ka tähele, et koefitsiendi “mitte-oluline” p väärtus ei tähenda iseenesest, et koefitsient tõenäoliselt võrdub nulliga või on nulli lähedal, vaid seda, et meil pole piisavalt andmeid, et vastupidist kinnitada. Koefitsiendi hinnangu usalduspiirid on selles osas palju parem töövahend.

Kui meie andmed on kolmedimensionaalsed (me mõõdame igal mõõteobjektil kolme muutujat) ja me tahame ennnustada ühe muutuja väärtust kahe teise muutuja väärtuste põhjal (meil on kaks prediktorit), siis tuleb meie kolme parameetriga lineaarne regressioonimudel tasapinna kujul. Kui meil on kolme prediktoriga mudel, siis me liigume juba neljamõõtmelisse ruumi.

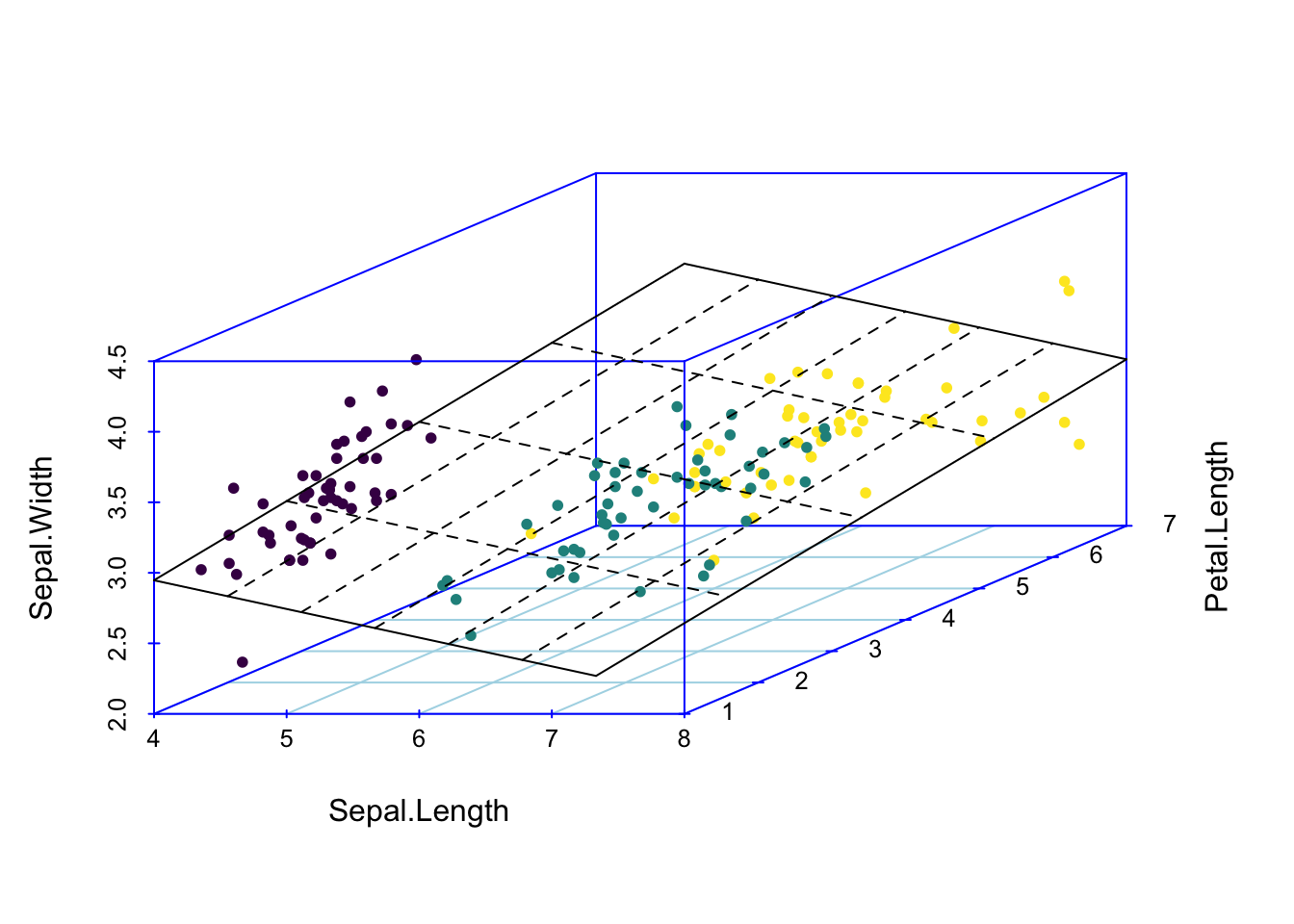
Regressioonitasand 3D andmetele. Kahe prediktoriga mudel, kus Sepal.Length ja Petal.Length on prediktorid ja Sepal.Width ennustatav muutuja.

Joonis 5.1: Regressioonitasand 3D andmetele. Kahe prediktoriga mudel, kus Sepal.Length ja Petal.Length on prediktorid ja Sepal.Width ennustatav muutuja.

Seda mudelit saab kaeda 2D ruumis, kui kollapseerida kolmas mõõde konstandile.

p <- ggplot(iris, aes(Sepal.Length, Sepal.Width, color = Species)) +
  geom_point() +
  xlim(4, 8) +
  scale_color_viridis(discrete = TRUE) +
  theme(title = element_text(size = 8))
p1 <- p + geom_abline(intercept = coef(m2)[1], slope = coef(m2)[2]) +
  labs(title = deparse(formula(m2)))
m1 <- lm(Sepal.Width ~ Sepal.Length, data = iris)
p2 <- p + geom_abline(intercept = coef(m1)[1], slope = coef(m1)[2]) +
  labs(title = deparse(formula(m1)))
devtools::source_gist("8b4d6ab6a333ef1cd14e8067c3badbae", filename = "grid_arrange_shared_legend.R")
grid_arrange_shared_legend(p1, p2)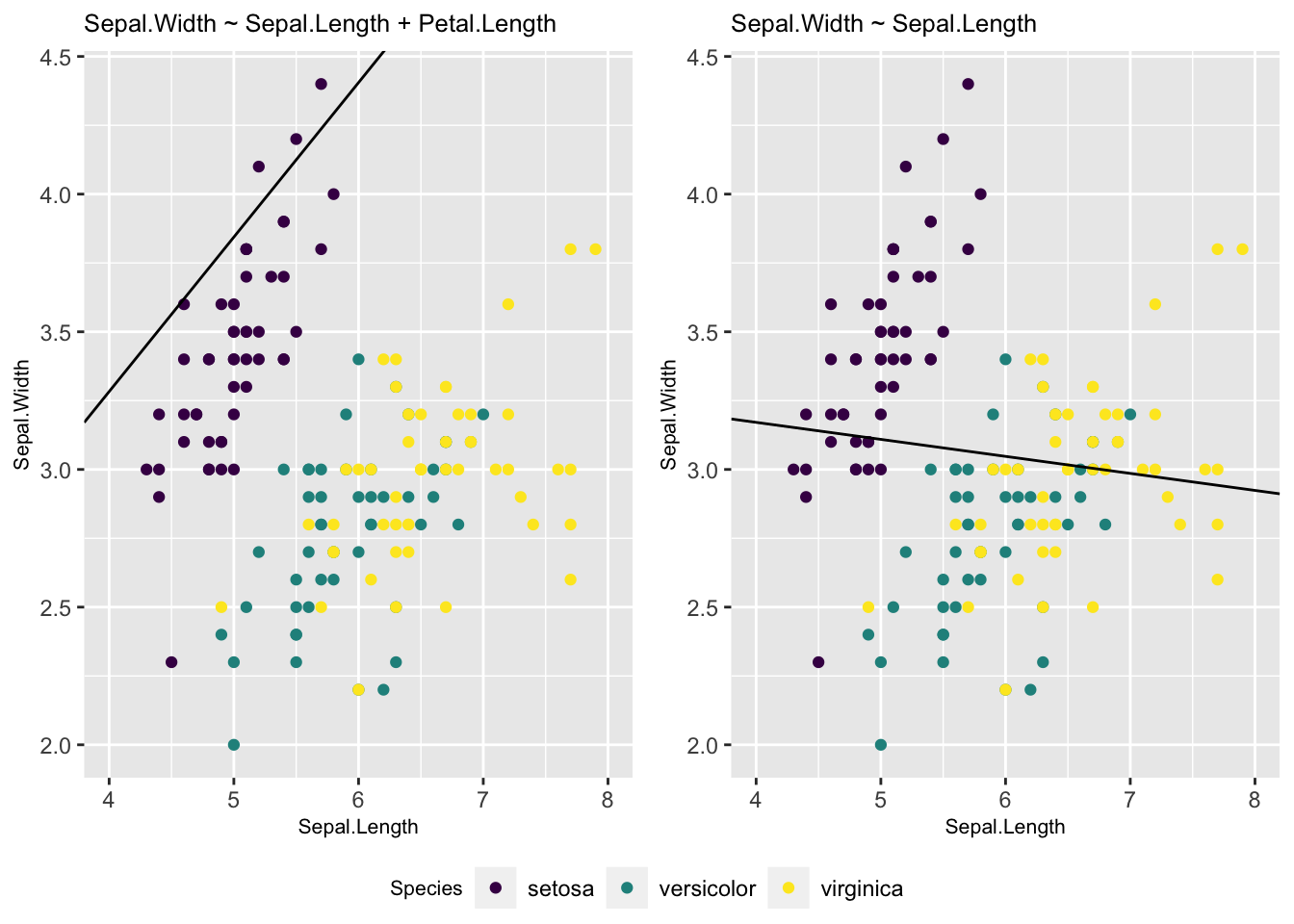

2D-le kollapseeritud graafiline kujutus 3D andmete põhjal fititud mudelist. Vasemal, muutuja Petal.Length on kollapseeritud konstandile. Siin on regressioonijoon hoopis teises kohas, kui lihtsas ühe prediktoriga mudelis (paremal).

Joonis 5.2: 2D-le kollapseeritud graafiline kujutus 3D andmete põhjal fititud mudelist. Vasemal, muutuja Petal.Length on kollapseeritud konstandile. Siin on regressioonijoon hoopis teises kohas, kui lihtsas ühe prediktoriga mudelis (paremal).

Võrreldes mudelite m1 (üks prediktor) ja m2 (kaks prediktorit) Sepal.Length ($b_1$) koefitsienti on näha, et need erinevad oluliselt.

coef(m1)
#>  (Intercept) Sepal.Length 
#>       3.4189      -0.0619
coef(m2)
#>  (Intercept) Sepal.Length Petal.Length 
#>        1.038        0.561       -0.335

Kumb mudel on siis parem? AIC-i järgi on m2 kõvasti parem kui m1, lisakoefitsendi (Petal.Length) kaasamisel mudelisse paranes oluliselt selle ennustusvõime.

AIC(m1, m2)
#>    df   AIC
#> m1  3 179.5
#> m2  4  92.1

Ennustused sõltumatute prediktoritega mudelist

Siin on idee kasutada fititud mudeli struktuuri ennustamaks y keskmisi väärtusi erinevatel $x_1$ ja $x_2$ väärtustel. Kuna mudel on fititud, on parameetrite väärtused fikseeritud.

## New sepal length values
Sepal_length <- seq(min(iris$Sepal.Length), max(iris$Sepal.Length), length.out = 10)
## Keep new petal length constant
Petal_length <- mean(iris$Petal.Length)
## Extract model coeficents
a <- coef(m2)["(Intercept)"]
b1 <- coef(m2)["Sepal.Length"]
b2 <- coef(m2)["Petal.Length"]
## Predict new sepal width values
Sepal_width_predicted <- a + b1 * Sepal_length + b2 * Petal_length

plot(Sepal_width_predicted ~ Sepal_length, type = "b", ylim = c(0, 5), col = "red")
# Prediction from the single predictor model
abline(m1, lty = "dashed")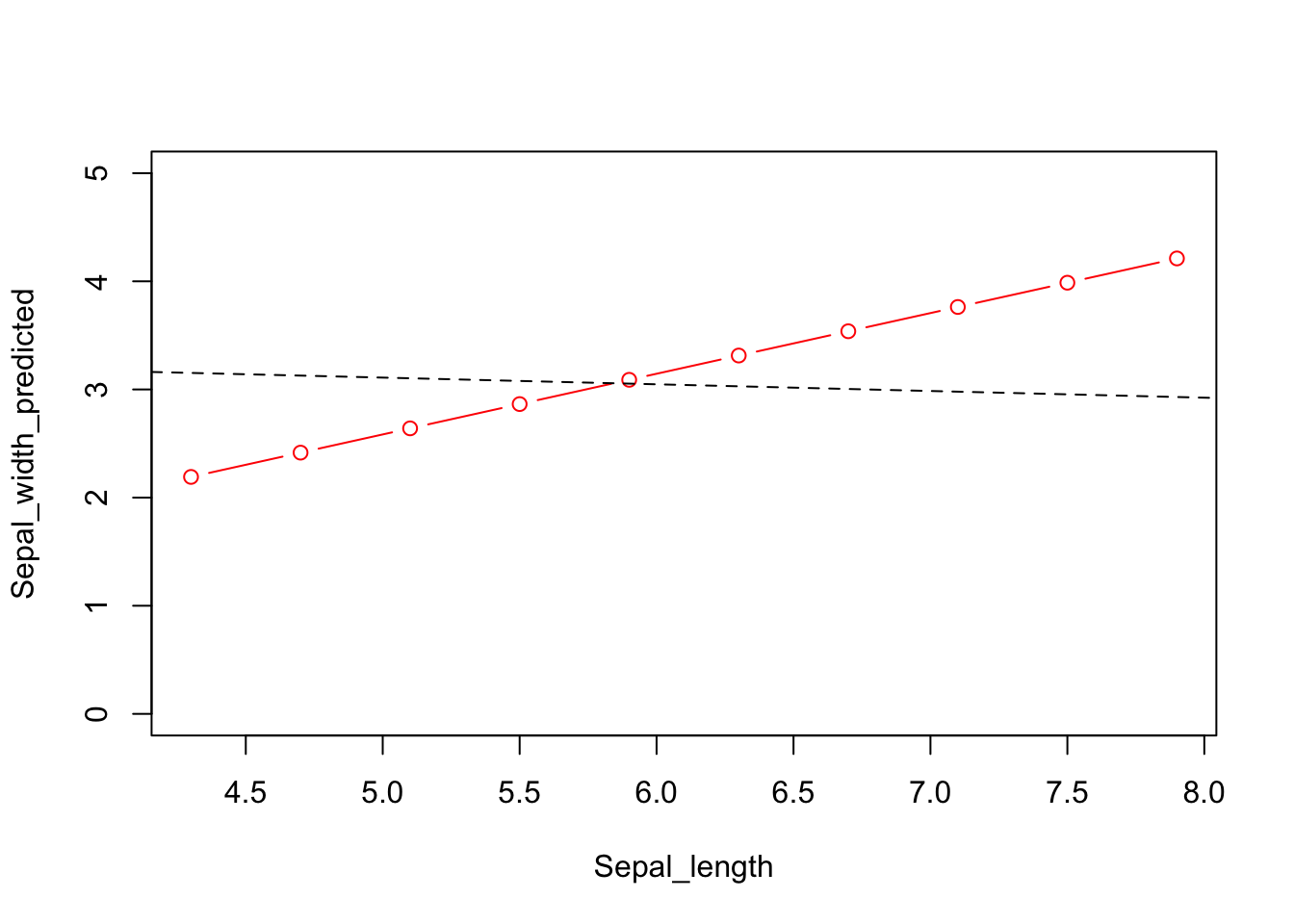

$Ennustatud y väärtused erinevatel $x_1$ väärtustel kui $x_2$ on konstantne, punane joon. Katkendjoon, ühe prediktoriga mudeli ennustus.$

Joonis 5.3: Ennustatud y väärtused erinevatel $x_1$ väärtustel kui $x_2$ on konstantne, punane joon. Katkendjoon, ühe prediktoriga mudeli ennustus.

Nüüd joonistame 3D pildi olukorrast, kus nii x₁ kui x₂ omandavad rea väärtusi. Mudeli ennustus on ikkagi sirge kujul – mis sest, et 3D ruumis.

#> Warning: `data_frame()` is deprecated, use `tibble()`.
#> This warning is displayed once per session.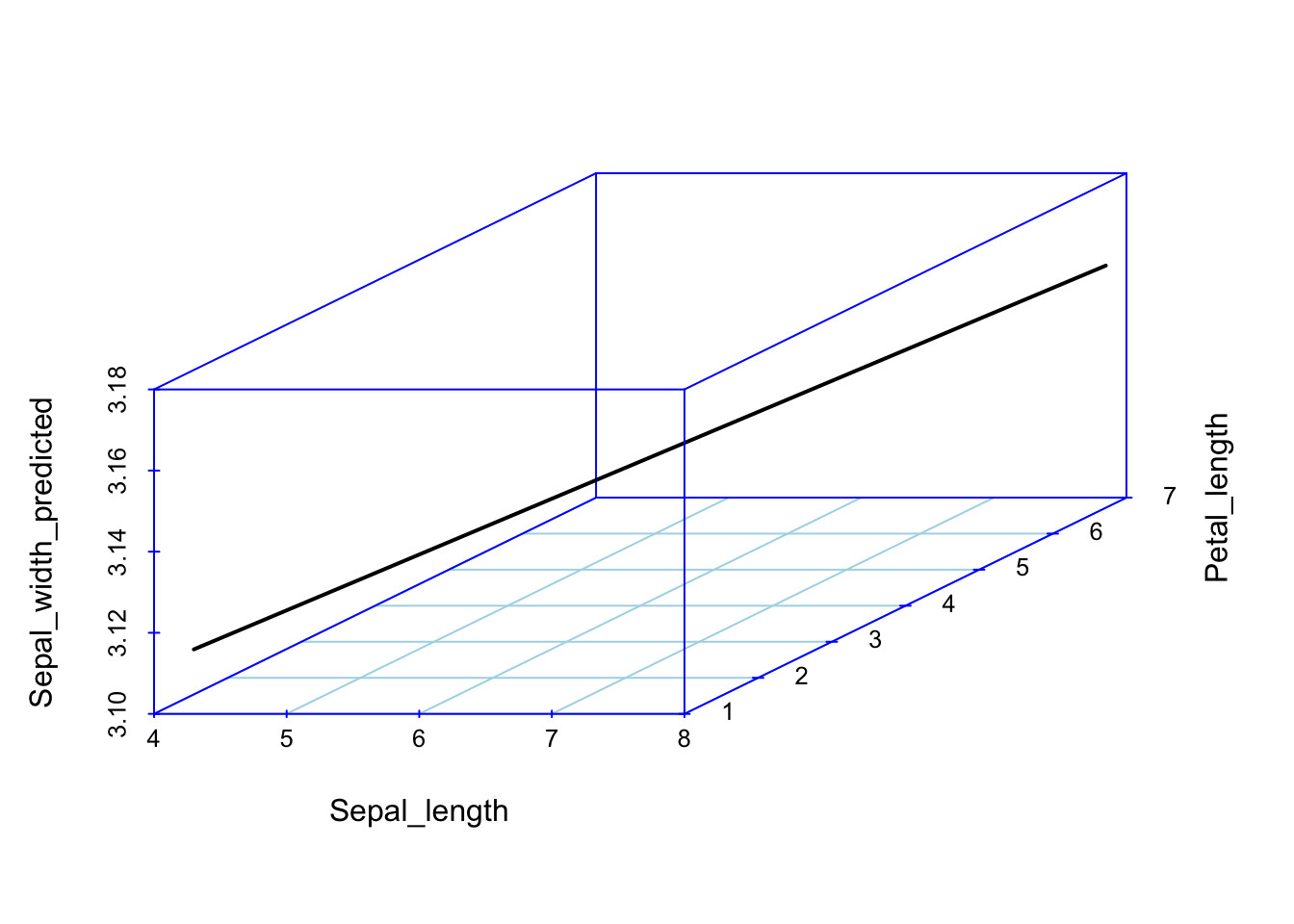

Joonis 5.4: Kahe prediktoriga mudeli ennustus 3D ruumis.

5.2 Interaktsioonimudel

Interaktsioonimudelis sõltub ühe prediktori mõju teise prediktori väärtusest:

\[y = a + b_1x_1 + b_2x_2 + b_3x_1x_2\]

Ekvivalntne viis interaktsiooni spetsifitseerida on läbi võrrandisüsteemi: \[y = a + \gamma x_1 + b_2x_2\] \[\gamma = b_1 + b_3x_2\] Siit on hästi näha, et me teeme kaks lineaarset regressiooni, millest teine modelleerib $x_1$ muutuja koefitsiendi sõltuvust $x_2$ muutuja väärtusest.

Samamoodi kehtib ka ümberkirjutus \[y = a + \gamma x_2 + b_1x_1\] \[\gamma = b_2 + b_3x_1\]

mis tähendab, et ühtlasi modelleerime me ka $x_2$ koefitsiendi sõltuvust $x_1$-st. Mudeli koefitsientide tõlgendamise teeb keeruliseks, et gamma tõlgendamisel tuleb arvesse võtta kolm asja – b₂, b₃ ja x₁.

Kaks muutujat võivad inteakteeruda sõltumata sellest, kas nad on korreleeritud või mitte – interaktsioon ei impitseeri korrelatsiooni, ega vastupidi.

Sageli on nii, et prediktoreid, mille mõju y-le on suur, tasub mudeldada ka interaktsioonimudelis (näiteks suitsetamise mõju vähimudelites kipub olema interaktsiooniga). Interaktsioonimudelis on b₁ koefitsient otse tõlgendatav ainult siis, kui x₂ = 0 (ja b₂ ainult siis, kui x₁ = 0).

Kui interaktsioonimudel fititakse tsentreeritud x-muutujate peal, mille keskväärtus = 0 (või standardiseeritud muutujatel), siis muutub koefitsientide tõlgendamine lihtsamaks:

b₁ annab y tõusu, kui x₁ tõuseb 1 ühiku võrra ja x₂ on fikseeritud oma keskväärtusel
b₂ annab y tõusu, kui x₂ tõuseb 1 ühiku võrra ja x₁ on fikseeritud oma keskväärtusel).
b₃ ütleb, kui palju muutub x₁ mõju y-le, kui x₂ muutub ühe ühiku võrra. Samamoodi, b₃ ütleb, kui palju muutub x₂ mõju y-le, kui x₁ muutub ühe ühiku võrra.

NB! Ärge standardiseerige faktormuutujaid ehk dummy-regressoreid kujul 1, 0 – neid on lihtsam tõlgendada algsel kujul 0/1 skaalas.

Edaspidi õpime selliseid mudeleid graafiliselt tõlgendama, kuna koefitsientide otse tõlgendamine ei ole siin sageli perspektiivikas.

Interaktsioonimudelis sõltub x₁ mõju tugevus y-le x₂ väärtusest. Selle sõltuvuse määra kirjeldab b₃ (x₁ ja x₂ interaktsiooni tugevus). Samamoodi ja sümmeetriliselt erineb ka x₂ mõju erinevatel x₁ väärtustel. Ainult siis, kui x₂ = 0, ennustab x₁ tõus 1 ühiku võrra y muutust b₁ ühiku võrra.

Kui meil on mudelis interaktsiooniliige $x_1x_2$, siis on enamasti mõistlik ka lisada eraldi liikmetena ka $x_1$ ja $x_2$.

Näiteks mudel, milles on pidev y-muutuja, pidev prediktor “education” ja binaarne prediktor “sex_male” (1 ja 0):

\[score = a + b_1 * education + b_2 * sex_{male} + b_3 * education * sex_{male}\]

Variandis

\[score = a + b_1 * education + b_3 * education * sex_{male}\]

surume meeste ja naiste intercepti pidevale muutujale “education” ühte punkti, aga samas modelleerime sellele erinevad tõusud meeste ja naiste lõikes.

Samamoodi, variandis

\[score = a + b_2 * sex_{male} + b_3 * education * sex_{male}\]

on naiste tõus surutud nulli, aga interceptid võivad erineda, mis on kokkuvõttes üsna imelik, kuigi tehniliselt on mudel ok ja seda võib edukalt fittida.

Ja variandis

\[score = 0 + b_3 * education * sex_{male}\]

On meil meeste ja naiste intercept surutud nulli, aga meeste ja naiste tõusud võivad erineda.

Kui meil on kaks faktor-prediktorit, siis mudel kujul

\[y= 0 + b_3x_1x_2\]

Mudeldab eraldi nende faktorite tasemete kõikvõimalud kombinatsioonid.

Oletame, et meil on lisaks pidevale prediktorile x₁ ka faktor-prediktor x₂. Diskreetsed e faktor-prediktorid rekodeeritakse automaatselt nn dummy-muutujateks. Kahevalentse e binaarse muutuja, näit sex = c(“male”, “female”), korral läheb regressioonivõrrandisse uus dummy-muutuja, sex_female, kus kõik emased on 1-d ja isased 0-d. Üldine intercept vastab siis isaste mõjule ja sex_female intercept annab emaste erinevuse isastest. Kui meil on n-tasemega diskreetne muutuja, rekodeerime selle n-1 dummy-muutujana, millest igaüks on 0/1 kodeeringus ja millest igaühe interceptid annavad erinevuse null-taseme (selle taseme, mis ei ole rekodeeritud dummy-muutujana) interceptist. Mudeli seisukohast pole oluline, millise faktortunnuse taseme me nulltasemeks võtame. Terminoloogiliselt on meie n-tasemega faktortunnus seletav muutuja (explanatory variable), millest tehakse n-1 regressorit. Seega tehniliselt on mudeli liikmed regressorid, mitte seletavad muutujad. Üks seletav muutuja võib anda välja mitu regressorit (nagu eelmises näites) ja üks regressor võib põhineda mitmel muutujal (näit x_1x2 interaktsiooniterm).

Interaktsioonimudeli 2D avaldus on kurvatuuriga tasapind, kusjuures kurvatuuri määrab b₃.

Interaktsiooniga mudel on AIC-i järgi pisut vähem eelistatud võrreldes kahe prediktoriga mudeliga m2. Seega, eriti lihtsuse huvides, eelistame m2-e.

m3 <- lm(Sepal.Width ~ Sepal.Length + Petal.Length + Sepal.Length * Petal.Length, data = iris)
AIC(m1, m2, m3)
#>    df   AIC
#> m1  3 179.5
#> m2  4  92.1
#> m3  5  93.4

Ennustused interaktsioonimudelist

Kõigepealt anname rea väärtusi x₁-le ja hoiame x₂ konstantsena.

Petal_length <-  mean(iris$Petal.Length)
a <- coef(m3)["(Intercept)"]
b1 <- coef(m3)["Sepal.Length"]
b2 <- coef(m3)["Petal.Length"]
b3 <- coef(m3)["Sepal.Length:Petal.Length"]
Sepal_width_predicted <- a + b1 * Sepal_length + b2 * Petal_length + b3 * Sepal_length * Petal_length
plot(Sepal_width_predicted ~ Sepal_length, type = "l", ylim = c(2, 6))
abline(coef(m2)[c("(Intercept)", "Sepal.Length")], lty = "dashed")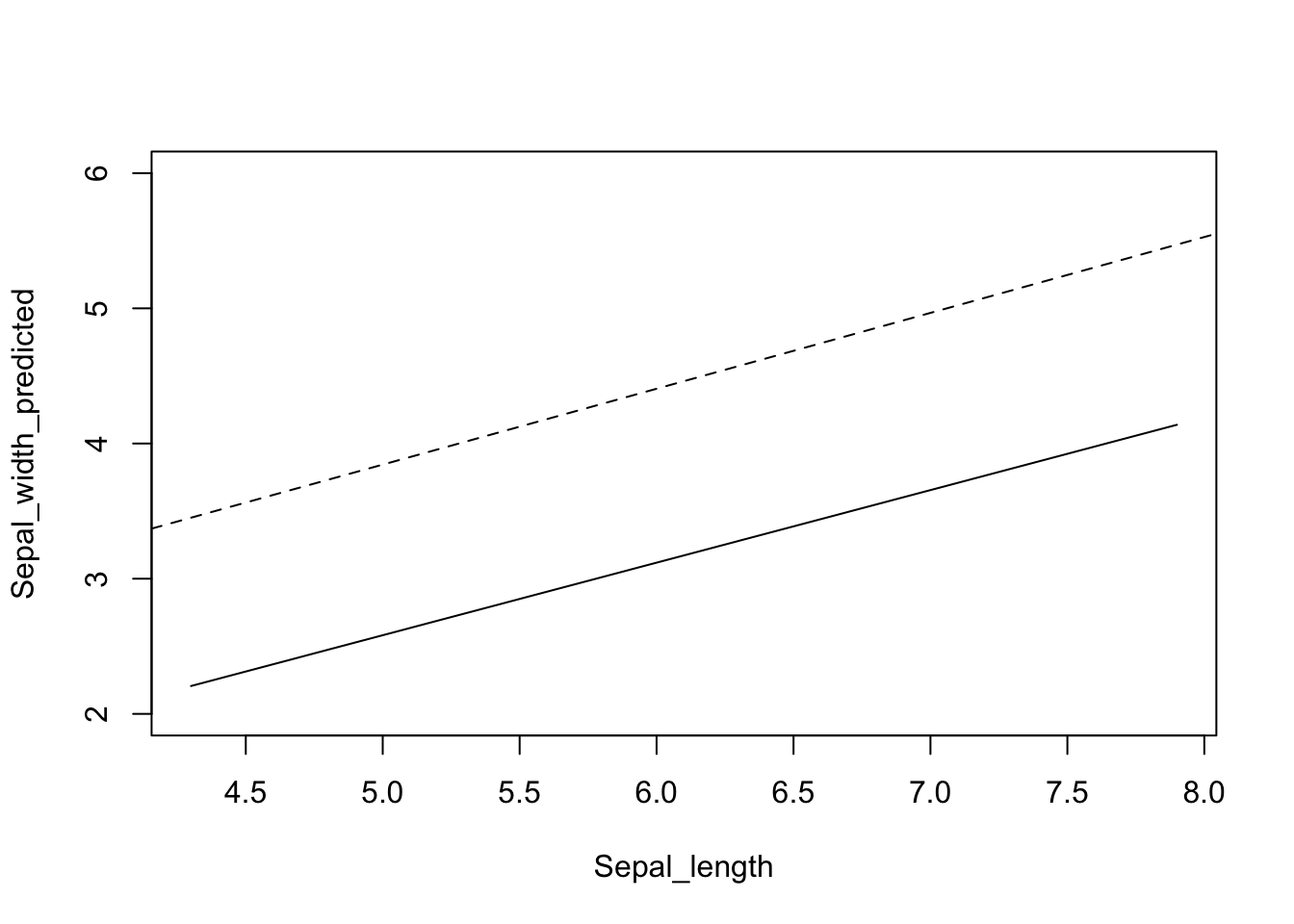

Ennustus interaktsioonimudelist, kus x1 (Sepal_Length) on antud rida väärtusi ja x2 (Petal_length) hoitakse konstantsena (pidevjoon). Interaktsioonimudeli regressioonijoon on paraleelne ilma interaktsioonita mudeli ennustusele (katkendjoon).

Joonis 5.5: Ennustus interaktsioonimudelist, kus x₁ (Sepal_Length) on antud rida väärtusi ja x₂ (Petal_length) hoitakse konstantsena (pidevjoon). Interaktsioonimudeli regressioonijoon on paraleelne ilma interaktsioonita mudeli ennustusele (katkendjoon).

Nagu näha viib korrutamistehe selleni, et interaktsioonimudeli tõus erineb ilma interaktsioonita mudeli tõusust.

Kui aga interaktsioonimudel plottida välja 3D-s üle paljude x₁ ja x₂ väärtuste, saame me regressioonikurvi (mitte sirge), kus b₃ annab kurvatuuri.

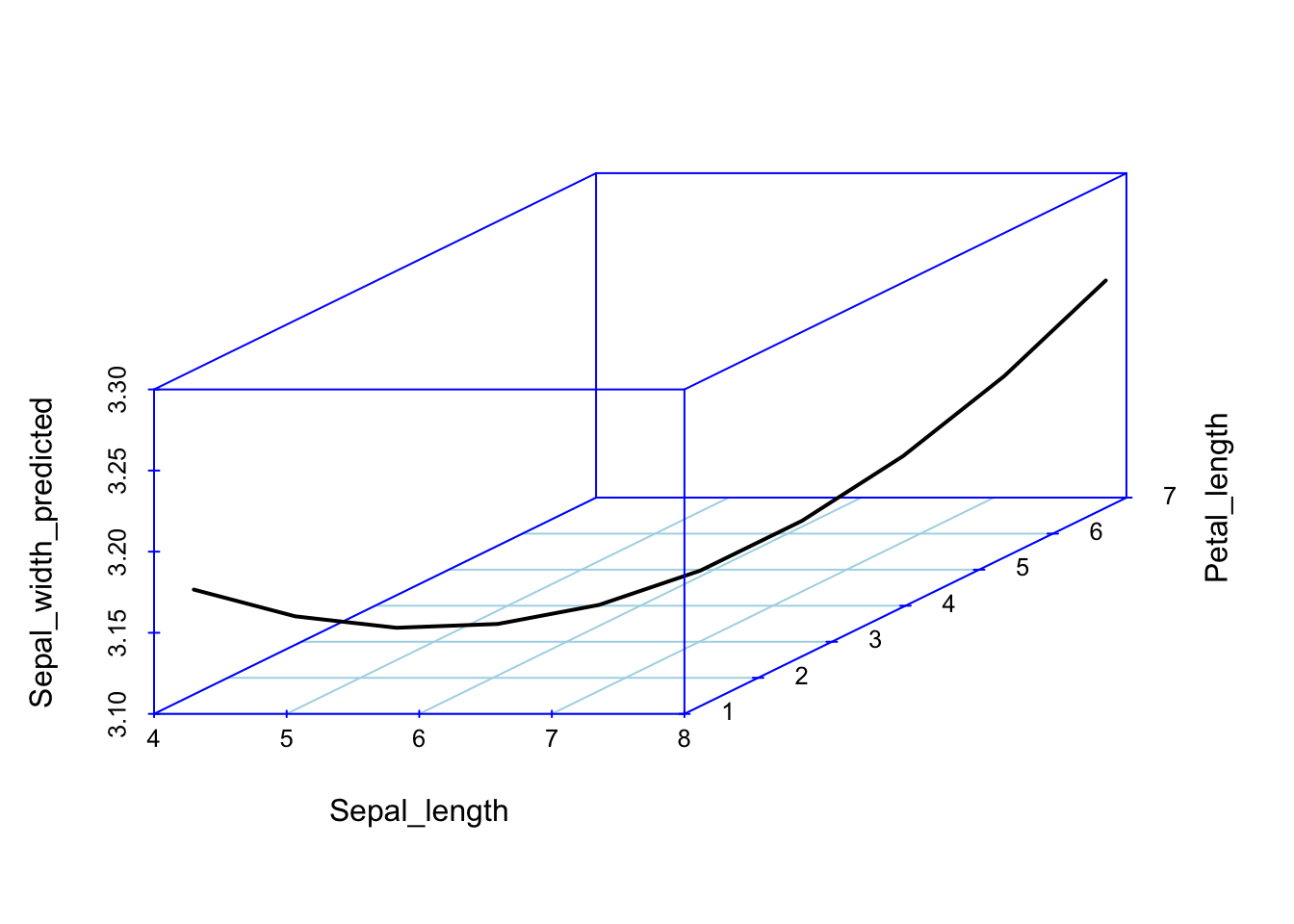
Ennustused 3D interaktsioonimudelist üle paljude x1 (Sepal_Length) ja x2 (Petal_length) väärtuste.

Joonis 5.6: Ennustused 3D interaktsioonimudelist üle paljude x₁ (Sepal_Length) ja x₂ (Petal_length) väärtuste.

Vau! See on alles ennustus!